
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение графиков линии регрессииСодержание книги
Поиск на нашем сайте
12. В ячейках С2 и D2 вычислить значение функции регрессии (значение переменной У по значению переменной Х) 13. =$F$13*A2+$G$13 - регрессия У на Х (уравнение
14. =(A2-$G$12)/$F$12 - регрессия Х на У (уравнение
15. Скопировать ячейки С2 и D2 параллельно данным столбца А 16. Написать уравнения регрессии X на Y (ячейка F15) 17. Написать уравнение регрессии Y на X (ячейка F16) 18. Выделить данные в столбцах A,B,C,D и вызвать мастер построения диаграмм. 19. Выбрать тип диаграммы «Точечная диаграмма со значениями, соединенными сглаживающими линиями» 20. После двух нажатий кнопки «Далее» выбрать закладку «Легенда» и удалить из графика легенду 21. Нажать на кнопку «Готово» 22. Привести вид полученного графика в соответствие с приведенным выше стандартом: 23. Убрать маркеры линии регрессии 24. Написать наименование осей
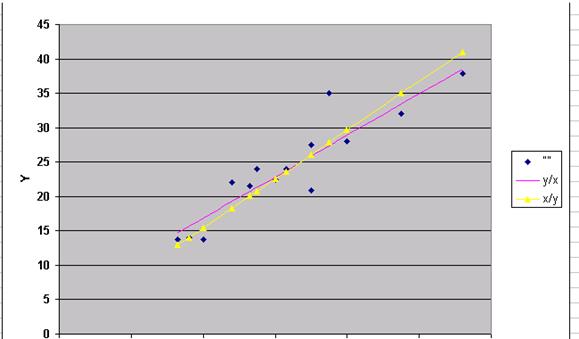
Ниже приводится иллюстрация результатов расчета и графика линий регрессии:
График линий регрессии
Имеются данные по 15 регионам, связывающие капиталовложения в млн. рублей и количеством автотранспортных происшествий
Найти коэффициент корреляции и построить линии регрессии одного из признаков по другому признаку. Задача 5.4. Имеются данные по 15 студентам, связывающие количество пропущенных занятий в часах и средний балл, полученный студентом по итогам сессии
Найти коэффициент корреляции и построить линии регрессии одного из признаков по другому признаку. Задача 5.5. Преподавателю и студенту было предложено расположить 15 профессий в порядке их восстребованности на рынке. В результате получилась следующая таблица:
Требуется оценить расхождение взглядов преподавателя и студента. В данном случае, поскольку значимость оценивается условным числом (рангом), для оценки меры связи используются статистики, не связанные с нормальным распределением(непараметрические статистики). В частности для оценки расхождения может использован коэффициент ранговой корреляции Спирмена
где
и определить критическое значение для правосторонней критической области при уровне значимости Список вопросов к зачету
1. Классификация различных типов выборок из множества 2. Правила суммы и произведения в комбинаторике 3. Повторные упорядоченные выборки (размещения с повторениями) 4. Бесповторные упорядоченные выборки (размещения) 5. Повторные неупорядоченные выборки 6. Бесповторные неупорядоченные выборки (Сочетания) 7. Понятие случайности. Классификация событий. Случайные события 8. Операции над событиями (объединение) 9. Операции над событиями (пересечение) 10. Операции над событиями (разность) 11. Операции над событиями (дополнение) 12. Операции над событиями (симметричная разность) 13. Полная группа событий 14. Определение вероятности 15. Свойства вероятности 16. Принцип практической невозможности маловероятных событий 17. Условная вероятность, понятие независимости событий 18. Формула полной вероятности 19. Формула Байеса 20. Понятие случайной величины 21. Математическое ожидание, свойства математического ожидания 22. Дисперсия, свойства дисперсии 23. Закон больших чисел 24. Функция распределения случайной величины. 25. Свойства функции распределения случайной величины 26. Плотность нормального распределения. 27. Корреляция. Коэффициент корреляции 28. Линия регрессии 29. Генеральная и выборочная совокупность. Репрезентативность выборки 30. Элементы математической статистики. Точечные оценки случайной величины. Свойства несмещенности, эффективности и состоятельности оценок. 31. Оценка математического ожидания 32. Оценка дисперсии 33. Ошибки статистического наблюдения 34. Зависимость переменных. Величина зависимости, надежность оценки 35. Шкалы измерений. Классификация шкал. 36. Доверительные интервалы 37. Проверка статистических гипотез. Нулевая и альтернативная гипотезы. 38. Критерии проверки статистических гипотез 39. Критическая область (правосторонняя, левосторонняя, двусторонняя). Критические точки. 40. Классификация ошибок в задаче проверки статистических гипотез
Примеры задач по теории вероятности:
1. Брошены две игральные кости. Найти вероятность того, что · сумма выпавших очков равна 4. · сумма выпавших очков равна 10 · сумма выпавших очков четная · сумма выпавших очков равна 8, а их разность 4 · сумма выпавших очков равна 5, а их произведение 4 2. Набирая номер телефона, абонент забыл последние две (три) цифры, но помнил при этом, что эти цифры различны и набрал их наугад. Найти вероятность того, что при случайном выборе последних цифр будет набран нужный номер. 3. В учебной группе 32 студента, из которых 6 студентов – отличники, 12 студентов – учится на 4 и 5, а 16 студентов имеют удовлетворительные оценки. Какова вероятность того, что вызванный студент не имеет троек? 4. Вероятность того, что стрелок при одном выстреле выбьет 10 очков равна 0,1; вероятность выбить девять очков – равна 0,3; выбить 8 или меньше – 0,6. Найти вероятность того, что стрелок выбьет не менее 9 очков. 5. На опознании пригласили шесть человек, причем двое из шести подозреваются в совершении преступления. Все пришедшие на опознание лица случайным образом встали в ряд. Необходимо определить вероятность того, что между подозреваемыми лицами окажутся ровно 2 человека. 6. В семье родилось 4 ребенка. Какое распределение мальчиков и девочек является наиболее вероятным? 7. Из колоды, содержащей 52 карты, вытащили 10 карт. Какова вероятность, что среди карт окажется · хотя бы один туз? · ровно один туз? · ровно два туза? 8. Брошены три игральные кости. Найти вероятности следующих событий: · На двух выпавших гранях появится одно очко, на третьей – другое. · На двух выпавших гранях появится одно число очков, на третьей – другое. · На всех выпавших гранях появится разное число очков · Сумма очков на первых двух костях больше количества очков на третьей кости 9. На стеллаже в библиотеке в случайном порядке расставлено 14 учебников, причем пять из них в переплете. Библиотекарь берет наугад три учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплете. 10. На опознании преступника пригласили 4 лиц, участвующих в эксперименте опознания. Оказалось, что все они разного роста. Найти вероятность того, что они рассядутся по росту 11. Студент знает 18 из 30 вопросов программы. Найти вероятность того, что студент знает предложенные ему экзаменатором три вопроса. 12. Два игрока 13. У Джонсонов 5 детей и все девочки. Верно ли утверждение, что более вероятным ждать 6-м ребенком мальчика? 14. Когда Костя Сидоров, ученик 6б класса, наконец-то обнаружил в буфете кулек с конфетами, он услышал, как отворилась входная дверь. Это пришла из магазина бабушка Пелагея Марковна. Времени на выбор не было, и Костя, запустив руку в кулек, едва успел переместить к себе в карман две конфеты. Какова вероятность того, что ему достался хотя бы один «Мишка на Севере», если в кульке было 7 конфет с помадкой, 5 соевых батончиков и 3 "Мишки на Севере"? 15. В зрительном зале забронировано 10 мест для приглашенных гостей. Пришли 8 приглашенных. Найти вероятность того, что четверо из пришедших гостей займут определенные для каждого из них места, если гости занимают места случайным образом. 16. Во время первой мировой войны солдаты на фронте во время артиллерийского обстрела предпочитали искать укрытие в свежих воронках от снарядов. Прятаться в старых воронках они считали рискованным, так как в них при очередном обстреле скорее может угодить новый снаряд. В свежей воронке солдаты какое-то время чувствовали себя в безопасности, так как считали совершенно невероятным, чтобы два снаряда попали подряд в одно и то же место. Эффективна ли такая тактика? 17. Чайный сервиз на 6 персон состоит из 6 чашек, 6 блюдец, чайника, сахарницы и молочника. Во время ссоры нигде не работающая Клава запустила в своего приятеля Григория тремя первыми попавшимися под руку предметами из сервиза. Какова вероятность того, что не пострадали чашки? (Указание: считать, что предметы попадались Клаве под руку совершенно случайно.) 18. Пустые горшочки из под меда Винни-Пух ставит на полочку вместе с полными для того, чтобы вид уменьшающегося числа горшков не слишком портил ему настроение. В настоящий момент в Пуховом буфете вперемежку стоят 5 горшочков с медом и 6 абсолютно пустых. Какова вероятность того, что в двух взятых наугад горшечках окажется мед? 19. Что является более вероятным: в семье с четырьмя детьми встретить трех мальчиков и одну девочку или трех девочек и одного мальчика, чем двух мальчиков и двух девочек или двух мальчиков и двух девочек? 20. Ученик 6б класса Костя Сидоров и его приятель, заняв выгодную позицию вблизи школьных дверей, обстреливали снежками всех выходящих девчонок. Когда дверь в очередной раз открылась, два снежка одновременно полетели в голову застывшего на пороге завуча - Маргариты Викентьевны. Какова вероятность поразить цель, если известно, что Костя обычно попадает 8 раз из 10, а его приятель только 7? 21. Для разрушения моста достаточно попадания одной авиационной бомбы. Найти вероятность того, что мост будет разрушен, если на него сбросить четыре бомбы, вероятности попадания которых соответственно равны 0.3, 0.4, 0.6, 0.7. 22. Вероятность хотя бы одного попадания в мишень при трех выстрелах равна 0,875. Найти вероятность попадания при одном выстреле 23. В электрическую цепь последовательно включены три элемента, работающие независимо друг от друга. Вероятности отказов элементов равны соответственно 0.1, 0.15, 0,2. Найти вероятность того, что тока в цепи не будет. 24. Их трех маршрутов автобусов А, Б и С для студента попутными являются автобусы маршрутов А и Б. Найти вероятность того, что к остановке первым подойдет автобус попутного маршрута, если по линии маршрутов А, Б и С курсируют соответственно 12, 8, 11 автомашин. 25. В фирме 400 работников. 350 из них имеют высшее образование, 240 – среднее специальное образование, а 300 сотрудников имеют и высшее, и среднее специальное образование. Чему равна вероятность того, что случайно вызванный работник имеет или среднее специальное, или высшее образование, или то и другое? 26. Ученик 6б класса Костя Сидоров и два его приятеля засели с рогатками в кустах школьного двора, чтобы пострелять по голубям, воркующим на карнизе окна директорского кабинета. Едва они сделали по одному выстрелу, как оконное стекло со звоном разлетелось, и всей компании пришлось спасаться бегством от выскочившего во двор завхоза. Какова вероятность, то разбитое окно дело рук Кости Сидорова, если из 10 выстрелов он обычно попадает 8 раз, а его приятели по 7? (Примечание: случай коллективного попадания в окно исключается.) 27. Любимое занятие двухлетней девочки Кати - срезать пуговицы с одежды. Пока мама готовила кашу, Кате удалось отстричь все 5 белых пуговиц с папиной пижамы и 3 черные пуговицы с маминого вечернего платья. Одну пуговицу Катя проглотила, а остальные засунула в глубокую щель между полом и плинтусом. За этим занятием ее и застала мама. С большим трудом мама сумела выковырять из щели 2 пуговицы. Какова вероятность, что платье можно привести в порядок, если одна запасная пуговица у мамы есть? 28. Три преподавателя принимают зачет в группе из 25 человек. Причем первый из них опрашивает семерых студентов, второй – восьмерых, а третий – десять человек (выбор студентов производится случайным образом из списка). Отношение трех преподавателей к слабо подготовившимся студентам различное: шансы сдать зачет таких студентов у первого преподавателя равны 40%, у второго – только 10%, а у третьего – 70 %. Найти вероятность того, что студент сдаст зачет? 29. Симпатичная студентка Люся Копейкина к зачету успела выучить только 10 вопросов из 20, но надеется, что в случае неудачи уговорит профессора Аркадия Аристарховича задать ей второй вопрос. По многолетним наблюдениям профессора можно разжалобить в двух случаях из трех, и это соотношение не меняется с годами. Каковы Люсины шансы сдать зачет? 30. Студент филфака Петя Чернышев ставит три ящика пива против двух, что, выучив 12 билетов из 30, он сдаст зачет по крайней мере со второго раза. Стоит ли его приятелю заключать пари? 31. Поставки некоторого продукта в город могут производиться из трех областей – в количестве 20%, 30% и 50% соответственно. Доля продукта высшего сорта в поставках равна 40%, 50% и 20 % соответственно. Какова вероятность купить продукт более низкого качества? 32. В пирамиде 15 винтовок, из которых 6 снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом равна 0,98; для винтовки без оптического прицела она равна 0,85. Стрелок поразил цель из наудачу взятой винтовки. Что вероятнее: стрелок стрелял из винтовки соптическим прицелом или без него? 33. Три стрелка произвели по выстрелу, причем две пули поразили мишень. Найти вероятность того, что третий стрелок поразил мишень, если вероятности попадания в цель первым, вторым и третьим стрелками соответственно равны 34. Том Сойер ставит свою дохлую крысу на веревочке против приятельского сломанного будильника, что при подбрасывании 6 монет выпадет 3 орла. Том считает, что шансы получить или не получить загаданный результат равны. Прав ли он? 35. Выборка задана в виде распределения частот
Найти распределение относительных частот, эмпирическую функцию распределения, выборочное среднее, выборочную дисперсию и выборочное средне-квадратичное отклонение 36. Выборка задана в виде распределения частот
Найти распределение относительных частот, эмпирическую функцию распределения, выборочное среднее, выборочную дисперсию
Оглавление Введение. 3 Литература. 6 Элементы теории вероятностей.. 7 Случайное событие и вероятность. 7 Определение вероятности. 10 Принцип практической невозможности маловероятных событий. 13 Формулы комбинаторики. 14 Условная вероятность. 18 Независимые события. 19 Свойства вероятности. 20 Формула полной вероятности. 21 Формула Байеса. 22 Случайная величина. 23 Математическое ожидание дискретной с.в. 26 Свойства математического ожидания. 26 Дисперсия дискретной с.в. 27 Свойства дисперсии. 28 Закон больших чисел. 28 Функция распределения случайной величины.. 29 Свойства функции распределения. 32 Односторонние и двухсторонние значения вероятностей. 34 Нормальное распределение. 35 Взаимосвязи случайных величин. 37 Парная корреляция. 37 Элементы математической статистики.. 39 Генеральная и выборочная совокупность. 42 Основные шкалы измерений. 44 Точечные оценки параметров распределения. 46 Интервальное оценивание. 53 Проверка статистических гипотез. 54 P – значение. 64 Исследование зависимости между двумя характеристиками. 65 Лабораторная работа. 71 Задание 1. Нахождение выборочных характеристик. 71 Задача 1.1. 71 Задача 1.2. 78 Задача 1.3. 79 Задача 1.4. 79 Задача 1.5. 80 Задача 1.6. 81 Задание 2 Построение гистограммы выборки. 82 Задача 2.1. 82 Задание 3 Проверка статистических гипотез. 86 Одновыборочный критерий Стьюдента. 86 Двухвыборочный критерий Стьюдента. 89 Критерий согласия хи-квадрат. 91 Задание 4. Интервальные оценки. 94 Задача 4.1. 94 Задача 4.2. 95 Задание 5. Исследование статистической зависимости между двумя характеристиками. 96 Анализ значения коэффициента корреляции. 96 Построение линий регрессии. 96 Список вопросов к зачету. 102 Примеры задач по теории вероятности.. 103 Оглавление. 107
[1] Пересечение событий и обозначается также через [2] В этом примере имеет место строгое включение, поскольку при четной сумме очков не обязательно совпадение очков выпавших граней. [3] Значений (1,6) и (6,1) различаются поскольку они связаны с выпадениями очков на разных костях) [4] Конечно, нужна какая-либо теория, которая связывает объем наблюдений и точность решения. [5] Из серии – «природу не обманешь»: Можно показать, что данная вероятность зависит только от числа выученных билетов и не меняется, сколько бы студентов перед собой наш студент не пропустил [6] Пример гипотетический. В реальной жизни факт причастности доказывается без применения теории вероятностей [7] Случайная величина не обязательно принимает числовые значения. Значениями случайной величины могут быть и последовательности чисел (вектора), и функции, и математические объекты иной природы, в частности, нечисловой. Однако наиболее часто рассматриваются вероятностные модели с числовыми значениями. Кроме того, во многих задачах, можно нечисловые значения кодировать числами и рассматривать числовые функции без возможности производить арифметические действия над их значениями. [8] Такое распределение называется биномиальным [9] Можно провести аналогию с тестированием программ: Если на тестовом примере программа работает неверно, то это означает присутствие ошибки. Правильность выполнения программы означает лишь то, что проверяемый тест не выявляет ошибку, но при этом и не гарантирует, что такая ошибка возможна. [10] в этом случае можно делать определенные выводы [11] Функция ДИСПР вычисляет дисперсию по формуле (смещенная оценка) в отличие от функции ДИСП (формула (несмещенная оценка)) [12] Функция СТАНДОТКЛОНП вычисляет дисперсию по формуле в отличие от функции СТАНДОТКЛОН (формула) [13] Внимание! Приведенная нумерация ячеек соответствует расположению выходной информации, приведенной на рисунке. При других вариантах размещения таблиц, необходимо скорректировать адреса соответствующих ячеек. [14] Это достаточно жесткое требование, которое требует дополнительной проверки с использованием статистических критериев, но мы, с целью упрощения будем предполагать его выполнение. [15] Для нормального распределения число степеней свободы положить k-3
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 383; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.157.203 (0.009 с.) |

 )
) )
)
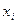
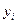
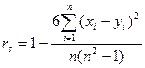 ,
,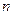 - число наблюдений, а
- число наблюдений, а 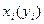 -
-  значения наблюдаемых данных. Для проверки гипотезы
значения наблюдаемых данных. Для проверки гипотезы  (связь отсутствует) при альтернативной гипотезе
(связь отсутствует) при альтернативной гипотезе 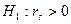 (существует положительная корреляционная зависимость) необходимо использовать статистику Стьюдента
(существует положительная корреляционная зависимость) необходимо использовать статистику Стьюдента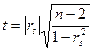
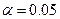
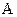 и
и  бросают по очереди две кости. Если сумма равна 7, то выигрывает
бросают по очереди две кости. Если сумма равна 7, то выигрывает 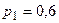 ,
, 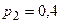 и
и 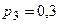
 1 6 8 12
1 6 8 12 5 2 3 1
5 2 3 1


