
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Генеральная и выборочная совокупностьСодержание книги
Поиск на нашем сайте
В статистических исследованиях ставится задача изучения совокупности однородных объектов относительно некоторого качественного или количественного признака, характеризующего эти объекты. (В качестве признака могут выступать температура человека, его рост, количество преступлений и т.д.). Качественные признаки обычно несут информацию о категориях, к которым можно отнести изучаемый объект и, в общем случае, могут выражаться нечисловыми (категоризованными) данными. Их нельзя складывать и умножать на коэффициенты. Математический аппарат анализа нечисловых статистических данных основан на использовании расстояний между элементами (а также мер близости или различия). С помощью расстояний определяются эмпирические и теоретические средние, доказываются законы больших чисел, строятся непараметрические оценки плотности распределения вероятностей, и т.д. Очень часто по различным причинам бывает невозможно провести сплошное обследование всех значений изучаемых параметров (например, проверить на таможне качество каждого ввозимого лекарственного препарата). В таких случаях в результате наблюдения за объектом формируется ограниченная по объему совокупность значений параметра, которую называют выборочной совокупностью. Объем выборочной совокупности – число значений этой совокупности. Совокупность всевозможных значений параметра, которые могут быть зарегистрированы в ходе неограниченного по времени наблюдения за объектом, называют генеральной совокупностью. Пусть из генеральной совокупности извлечена выборка:
Здесь При построении выборки приходится решать следующие важные задачи: · обеспечение случайного отбора вариант из генеральной совокупности (все элементы генеральной совокупности должны иметь одинаковые шансы попасть в выборку); · обеспечение репрезентативности (представительности) выборки, характеризующей в какой степени отобранные данные отражают структуру генеральной совокупности; · определение необходимого объема выборки для формирования статистически значимого заключения по результатам проведенных исследований. Например, довольно сложно оценить ситуацию по определенным видам правонарушений по всей стране. В этом случае можно рассмотреть один или несколько регионов, провести анализ соответствующих показателей, и затем попытаться результаты исследований распространить на все регионы. На этом пути возникают определенные вопросы: Насколько правомерно результаты, полученные по одному региону переносить на другой регион? Ведь регионы отличаются по экономическим, этнографическим, историческим и другим показателям. Какой объем выборки считать достаточным, для получения результатов с определенной степенью надежности. Понятно, что исследование одного индивида в отдельности не позволяет делать вывод о состоянии общества для региона в целом. Какое количество правонарушений должно быть обследовано, чтобы гарантировать определенную надежность результатов обследования. Эти вопросы довольно сложны, требуют тщательного анализа и выходят за круг вопросов, рассматриваемых в данном курсе. С другой стороны совершенно ясно, что невозможно проверить все данные, и приходится принимать решения на основе анализа части имеющихся в наличии данных, заранее соглашаясь при этом на возможность ошибочного вывода. Основные шкалы измерений Как уже отмечалось выше, не все данные могут быть представлены в обычном числовом виде с возможностью выполнения арифметических операций. Например, совершенно бессмысленно умножать или складывать ИНН, номера телефонов. Для классификации данных используется различные шкалы: 1. Номинальная. В этой шкале числа используются лишь как метки. Примерами в такой шкале являются номера телефонов, автомашин, паспортов. Пол людей также измеряется в этой шкале и принимает два значения - мужской, женский. Раса, национальность, цвет глаз, волос - номинальные признаки. Операции в номинальной шкале ограничиваются функцией отождествления объектов ( 2. Порядковая. В порядковой шкале числа используются не только для различения объектов, но и для установления порядка между объектами. Простейшим примером являются оценки знаний учащихся. С использованием оценок можно проводить ранжирование учащихся по успеваемости. Мы понимаем, что отличная оценка лучше, чем тройка. Но нельзя утверждать, что знания отличника являются суммой знаний троечника и двоичника. Порядковыми шкалами являются – уровень жизни ("низкий", "средний", "высокий"), шкала силы землетрясений. Операции отождествления объектов в этой шкале пополняются операциями сравнения 3. Интервальная (относительная). Интервальная шкала представляет шкалу количественных признаков, над которыми могут выполняться арифметические действия. В этой шкале можно найти разницу между двумя отчетами, но отсутствует понятие начальной точки отчета и масштаба измерений. Можно говорить, что числа 20 и 15, а также 30 и 25 одинаково отстоят друг от друга, но нельзя указать во сколько раз число 30 больше 25. 4. Абсолютная. Абсолютные переменные очень похожи на интервальные. В этих шкалах в дополнение ко всем свойствам переменных, заданных в интервальной шкале, характерной чертой является наличие определенной точки – абсолютного нуля и масштаба измерения. Поэтому в этой шкале можно говорить, что число 300 в три раза больше числа 100. Часто в порядковых, интервальных и абсолютных шкалах к данным применяют операцию ранжирования (упорядочивания) данных. В зависимости от типа данных применяются совершенно разные статистические методы их обработки. Значение параметра, вычисленное по ограниченному объему данных, является случайной величиной, поскольку значение такой величины от выборки к выборке может меняться заранее непредвиденным образом. Следовательно, в результате обработки данных определяется не точное значение параметра, а только лишь его приближенное значение – статистическая оценка параметра. Различают два вида оценок – точечные и интервальные. Точечными называют такие оценки, которые характеризуются одним числом. При малых объемах выборки точечные оценки могут значительно отличаться от истинных значений параметров, поэтому их вычисляют при большом объеме выборки, обычно
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 348; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.137.96 (0.011 с.) |

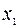





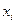 - это значение анализируемого параметра, а
- это значение анализируемого параметра, а 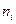 - количество анализируемых объектов, для которых это значение наблюдается. Полный объем выборки составляет
- количество анализируемых объектов, для которых это значение наблюдается. Полный объем выборки составляет  . Довольно часто значения
. Довольно часто значения 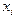 упорядочиваются по возрастанию. В этом случае, наблюдаемые значения
упорядочиваются по возрастанию. В этом случае, наблюдаемые значения  – относительными частотами. Статистическим распределением выборки называют перечень вариант и соответствующих им частот. Для наглядности часто строят различные графики статистического распределения (полигоны частот и гистограммы). Пусть
– относительными частотами. Статистическим распределением выборки называют перечень вариант и соответствующих им частот. Для наглядности часто строят различные графики статистического распределения (полигоны частот и гистограммы). Пусть  – количество наблюдений, при которых случайные значения параметра
– количество наблюдений, при которых случайные значения параметра  меньше
меньше  . Частость события
. Частость события  равна
равна  . Это отношение является функцией от
. Это отношение является функцией от  . Величина
. Величина 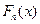 обладает всеми свойствами функции распределения:
обладает всеми свойствами функции распределения:  – наименьшее значение параметра, а
– наименьшее значение параметра, а  – наибольшее, то
– наибольшее, то 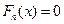 , когда
, когда  , и
, и  , когда
, когда  . Функция
. Функция 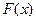 генеральной совокупности называют теоретической функцией распределения, она характеризует не частость, а вероятность события
генеральной совокупности называют теоретической функцией распределения, она характеризует не частость, а вероятность события  ). Номинальные шкалы позволяют проводить группировки данных по определенным значениям признаков.
). Номинальные шкалы позволяют проводить группировки данных по определенным значениям признаков. . Порядковые шкалы позволяют проводить упорядочивание объектов, но при этом не всегда можно определить насколько одно значение признака больше или меньше другого.
. Порядковые шкалы позволяют проводить упорядочивание объектов, но при этом не всегда можно определить насколько одно значение признака больше или меньше другого. . Интервальные оценки задаются двумя числами, определяющими вероятный диапазон возможного значения параметра. Эти оценки применяются для малых и для больших выборок.
. Интервальные оценки задаются двумя числами, определяющими вероятный диапазон возможного значения параметра. Эти оценки применяются для малых и для больших выборок.


