
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип практической невозможности маловероятных событийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Особую роль в статистических исследованиях играют практически невозможные (и сопутствующие им практически достоверные) события. Ни один прогноз в области случайных явлений не является и не может являться полностью достоверным; он может быть только практически достоверным, т. е. осуществляться с очень большой вероятностью. В основе применения всех выводов и рекомендаций, добываемых с помощью теории вероятностей, лежит принцип практической уверенности, который можно сформулировать следующим образом: Если вероятность события А в данном опыте весьма мала, то (при однократном выполнении опыта) можно вести себя так, как будто событие А вообще невозможно, т. е. не рассчитывать на его появление. В повседневной жизни мы постоянно (хотя и бессознательно) пользуемся этим принципом. Например, выезжая куда-то на поезде, мы не рассчитываем на возможность погибнуть в дорожной катастрофе, хотя некоторая (весьма малая) вероятность этого события все же имеется. Насколько маленькой должна быть вероятность события, чтобы это событие можно было считать практически невозможным? Ответ на этот вопрос выходит за рамки математической теории и в каждом отдельном случае решается из практических соображений в зависимости от сферы приложений полученных результатов. Чем более опасными являются последствия возможной ошибки предсказания, тем ближе к нулю должна быть вероятность события, чтобы его считать практически невозможным. Например, заложенная в проекте строительства атомной станции, вероятность 0,01 того, что здание не разрушится при природных катаклизмах, считается абсолютно недопустимой, но такая же вероятность ошибки при прогнозировании погоды может считаться приемлемой. Остаточно малую вероятность, при которой (применительно к данной определенной задаче) событие можно считать практически невозможным, называют уровнем значимости. На практике уровень значимости обычно заключен между 0,01 и 0,05. Формулы комбинаторики
Для подсчета вероятности события Набор элементов Упорядоченные Если элементы упорядоченной Неупорядоченная Если элементы неупорядоченной выборки попарно различны, она называется сочетанием (без повторений) из Пример 1.5. Пусть · девять размещений с повторениями – · шесть размещений без повторений – · шесть сочетаний с повторениями – · три сочетаний без повторений – В первом случае, перечисляются всевозможные пары элементов из множества Фундаментальную роль в решении перечислительных задач комбинаторики играют правило суммы и правило произведения: Правило суммы заключается в следующем: Если существует разбиение множества изучаемых комбинаций на классы (каждая комбинация содержится ровно в одном классе), то общее число комбинаций равно сумме комбинаций, входящих в каждый из классов. При наличии 2 классов правило суммы можно интерпретировать так: если объект Правило произведения можно сформулировать следующим способом: Если объект типа Пример 1.6. Пусть имеется схема дорожного сообщения между населенными пунктами Решение. Разобьем множество всех вариантов на два подмножества: Пример 1.7. Посчитать число двоичных последовательностей длины Решение: Каждый элемент последовательности может независимо от окружения принимать одно из двух значений 0 или 1. Применяя правило произведения, и учитывая длину последовательности, получаем, что число последовательностей равно произведению Обозначим через Теорема. Пусть производится выборка 1) 2) 3) 4) Пример 1.8. Пассажир забыл пароль камеры хранения на вокзале. Каково максимальное число вариантов необходимо перебрать, если пароль содержит 5 символов, набираемых в алфавите из 32 символов? Решение: При наборе каждого символа последовательности открывающей код камеры необходимо сделать выбор из 32 символов алфавита. Всего отбирается 5 символов, причем один и тот же символ может встречаться в набираемой последовательности многократно. При этом порядок следования символов в пароле важен. Имеем случай размещений с повторениями с параметрами Пример 1.9. Сколько существует способов рассадить на опознании группу из 6 человек в ряд вдоль стены? Решение: Имеется 6 мест, на которые необходимо рассадить 6 человек. Ни один человек не может одновременно занимать два места. Из условия задачи следует, что порядок выбора существенен. Имеем схему размещений без повторений с параметрами: Пример 1.10. Сколько существует способов отобрать 4-х студентов на сельхоз-работы из группы 9 студентов? Решение: Из условия задачи следует, что важно назвать отобранных студентов, а порядок отбора не важен, кроме того, один и тот же студент не может быть отобран более одного раза. Имеем схему без повторений, порядок следования не важен. Тогда ответ задачи в соответствии с теоремой описывается числом: Пример 1.11. Сколько существует способов разделить наследство в 100 рублей с точностью до рубля между 10 наследниками? Решение: Расположим 100 рублей по рублю в ряд, и проставим 9 меток между ними. Выбор меток определяет распределение наследства суммы между наследниками. Сумма, которая находится левее первой метки, достанется первому наследнику, между первой и второй – второму, и т.д. Все, что лежит правее последней девятой метки, отходит 10 наследнику. При совпадении двух меток, соответствующий наследник ничего не получает. Поэтому наследодателю необходимо определить положения 9 меток (метки повторяются, поэтому имеем повторную выборку) между 100 позициями (учитывая расположение меток, всего позиций - 109), порядок выбора меток несущественен. Имеем неупорядоченную Разберем несколько примеров подсчета вероятности по формуле (1). Пример 1.12. В коробке шесть одинаковых занумерованных кубиков. Найти вероятность того, что номера извлеченных кубиков появятся в возрастающем порядке. Решение: Обозначим через Пример 1.13. В группе 12 студентов, из них 5 отличников. По списку, наудачу, отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов – три отличника. Решение: Возможность числа вариантов выбора 9 студентов из 12 описывается формулой Условная вероятность
Условную вероятность определяется лишь для событий B, вероятность которых не равна нулю. Пример 1.14. Кубик подбрасывается один раз. Известно, что выпало более трех очков. Какова при этом вероятность того, что выпало четное число очков? Решение: Обозначим через Другое решение задачи получается с использованием формулы, определяющей условную вероятность. Мы хотим вычислить отношение числа исходов, благоприятствующих Из вышесказанного следует, что
Независимые события Важным понятием теории вероятностей является независимость. События A и B называются независимыми, если
т.е. вероятность одновременного осуществления этих событий равна произведению их вероятностей. Легко видеть, что и Пример 1.15. Найти вероятность совместного поражения цели двумя стрелками, если вероятность поражения цели первым стрелком равна 0,7, а вторым – 0,6. Решение: При одновременной стрельбе по цели двух стрелков событие Отметим, что если независимы события События
События Независимые в совокупности события независимы и попарно. Обратное неверно. Пример 1.16. Являются ли зависимыми события извлечь из колоды, содержащей 32 карты – туза и карту червовой масти? Решение: Из колоды карт в 32 листа извлекается одна карта. Пусть А – событие, состоящее в том, что извлечённая карта – туз. Событие В состоит в том, что извлечённая карта червовой масти. Очевидно, что Р(А)=4/32=1/8, и Р(В)=8/32. Поскольку вероятность извлечения из колоды червового туза равна
Свойства вероятности
1. вероятность принадлежит интервалу [0,1]. Вероятность достоверного события равна 1, невозможного события – равна нулю 2. сумма вероятностей некоторого события и его дополнения равна 1
3. свойство монотонности вероятности 4. вероятность объединения событий: Пример 1.17. Два стрелка сделали по одному выстрелу. Найти вероятность поражения цели ровно одним стрелком в тире, если вероятность попадания первого стрелка 0,6, а второго – 0,7. Решение: Обозначая через А – событие: попадание первого стрелка, через В – соответственно для второго стрелка, учитывая независимость событий, будем иметь, что искомая вероятность складывается из вероятностей двух событий:
Тогда, Пример 1.18. Найти вероятность вытащить туза или червовую масть при случайном отборе одной карты из колоды в 32 листа. Решение: Поскольку колода содержит по 4 карты одинакового ранга и по восемь карт одной масти, имеем Р(ТУЗ) = 4/32 = 1/8; Р(ЧЕРВОВАЯ МАСТЬ) = 8/32 = 1/4; Однако имеется одна карта ТУЗ ЧЕРВЕЙ, которая обладает каждым из этих свойств: Вероятность вытащить эту карту равна Р(ТУЗЧЕРВЕЙ)=1/32; Тогда
Пример 1.19. Три стрелка стреляют в мишень. Первый стрелок попадает в мишень с вероятностью 0,9, второй – с вероятностью 0,8, а третий – с вероятностью 0,7. Найти вероятность того, что мишень будет поражена? Решение: Для решения задачи можно использовать формулу сложения вероятностей. Однако с ростом числа событий эта формула усложняется. С другой стороны, несложно заметить, что событие, попадания в мишень хотя бы одного стрелка, является дополнением события, что мишень после выстрелов останется непораженной (событие
Формула полной вероятности
Из определения следует, что все события, составляющие полную группу, попарно несовместны:
Приведенная формула называется формулой полной вероятности. Пример 1.20. Студент перед зачетом выучил 20 вопросов из 25. Каждый билет содержит ровно один вопрос из программы. Каким по порядку (первым или вторым) лучше сдавать зачет, при условии, что каждый студент может отвечать только по одному выбранному билету, и каждый билет может быть выбран студентами ровно один раз(выбранный билет обратно не возвращается)? Решение: Имеем две стратегии сдачи зачета. Обозначим через При условии, что студент сдает зачет вторым по порядку, возможны следующие события:
Формула Байеса Пусть событие
При условии, что событие
Вероятности Пример 1.21. [6] Пусть известно, что преступление могло быть совершено ровно одним из двух подозреваемых лиц (события Решение: Мы находимся в условиях формулы Байеса. Имеем:
Как мы видим, следственный эксперимент в небольшой степени снял подозрения с первого лица. Случайная величина
При применении методов теории вероятностей исследователь чаще всего имеет дело с числовыми характеристиками наблюдаемого объекта, которые являются функциями элементарных исходов состояния объекта. Случайной называют числовую функцию[7], которая определена на множестве элементарных исходов. Примерами случайных величин являются: 4.1. Число родившихся мальчиков среди двухсот новорожденных является случайной величиной, принимающей значения от 0 до 200. 4.2. Число преступлений совершаемых за определенный период в некотором мегаполисе является случайной величиной, для значения которой мы можем дать только нижнюю оценку (значения ограничены снизу нулем). 4.3. Температура человеческого тела является также случайной величиной с бесконечным множеством значений. 4.4. Симметричная монета подбрасывается 3 раза. Число выпавших гербов является случайной величиной, которая принимает значения 0,1,2,3. Дискретной называют случайную величину (с.в.), которая принимает отдельные изолированные значения с определенными вероятностями. Число возможных значений с.в. может быть конечным или бесконечным (примеры 4.1 и 4.2.). Непрерывной называют случайную величину, которая принимает все значения из некоторого конечного или бесконечного промежутка. Число возможных значений непрерывной с.в. бесконечно (пример 4.3). Для задания с.в. необходимо перечислить множество ее значений с указанием вероятностей этих значений. Законом распределения дискретной с.в. называют соответствие между возможными значениями и их вероятностями. При табличном задании с.в. получаем
где набор Распределение случайной величины можно задать различными способами: · в виде таблицы значений величины и соответствующих им вероятностей · в виде формулы: · в виде диаграммы: Рассмотрим пример 4.4. При трехкратном подбрасывании симметричной монеты и анализе возможных результатов эксперимента мы имеем 8 элементарных событий, которые приведены в таблице
Интересующая нас случайная величина задается в виде таблицы
Для той же самой случайной величины распределение вероятностей может быть описано в виде формулы. Обозначим через Третий вариант задания распределения случайной величины является графическим. Случайная величина задается специальным графиком (гистограммой). Гистограмма строится таким образом, что площадь каждого прямоугольника при равных основаниях была пропорциональна вероятностям распределения данной с.в. Ниже приведен пример гистограммы распределения нашей случайной величины
Случайные величины
Математическое ожидание дискретной с.в. Математическим ожиданием случайной величины X называется число вида
где Пример 1.22: Найти математическое ожидание числа появлений события Решение. Построим случайную величину Таким образом, математическое ожидание числа появлений события в одном испытании равно вероятности этого события. Пример 1.23: Найти математическое ожидание для случайной величины, описанной в примере 4.4. Решение. Используя таблицу описания случайной величины, имеем
Смысл математического ожидания заключается в следующем: это точка на числовой оси, относительно которой группируются результаты конкретных испытаний над случайной величиной, она приближенно равна среднему арифметическому числа наблюдаемых значений случайной величины (некоторое подобие центра тяжести в механике).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 1230; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.57.57 (0.01 с.) |

 с использованием классической схемы необходимо уметь определять число всех событий, составляющих пространство элементарных событий, а также число элементарных событий, составляющих событие
с использованием классической схемы необходимо уметь определять число всех событий, составляющих пространство элементарных событий, а также число элементарных событий, составляющих событие 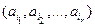 из
из 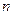 –элементного множества
–элементного множества  называется выборкой объема
называется выборкой объема 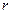 из
из  -выборкой. Выборка называется упорядоченной, если зафиксирован порядок следования элементов в ней. Две упорядоченные выборки, различающиеся лишь порядком следования элементов (выборки (1,3,5) и (5,1,3)), считаются различными. Если порядок следования элементов не является существенным, то выборка называется неупорядоченной. В выборках могут допускаться или не допускаться повторения элементов из основного набора.
-выборкой. Выборка называется упорядоченной, если зафиксирован порядок следования элементов в ней. Две упорядоченные выборки, различающиеся лишь порядком следования элементов (выборки (1,3,5) и (5,1,3)), считаются различными. Если порядок следования элементов не является существенным, то выборка называется неупорядоченной. В выборках могут допускаться или не допускаться повторения элементов из основного набора. .
. .
. .
. . Число сочетаний из
. Число сочетаний из  .
. и необходимо построить выборку из 2 элементов,
и необходимо построить выборку из 2 элементов,  . Тогда имеются:
. Тогда имеются: ;
; ;
; ;
; .
.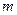 способами, а объект
способами, а объект 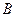 – другими
– другими 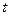 способами при условии, что одновременный выбор
способами при условии, что одновременный выбор  способами.
способами.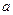 можно выбрать
можно выбрать  можно выбрать
можно выбрать  можно осуществить
можно осуществить 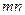 способами.
способами. (3 дороги соединяют
(3 дороги соединяют  (5 дорог соединяют
(5 дорог соединяют 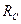 - множество дорог, ведущее от
- множество дорог, ведущее от  - множество дорог, ведущее от
- множество дорог, ведущее от  задачи для случаев
задачи для случаев 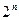 .
.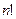 произведение всех целых чисел от 1 до
произведение всех целых чисел от 1 до  . Приведем без доказательства следующий результат:
. Приведем без доказательства следующий результат:



 . Тогда
. Тогда 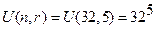 .
.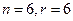 . Поэтому количество вариантов равно
. Поэтому количество вариантов равно 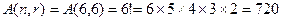

 -выборку, в которой элементы могут повторяться. Ответ определяется выражением
-выборку, в которой элементы могут повторяться. Ответ определяется выражением  , которое является достаточно большим числом и здесь не приводится.
, которое является достаточно большим числом и здесь не приводится. . Комбинация, составляющая событие А, имеется в единственном виде (
. Комбинация, составляющая событие А, имеется в единственном виде (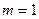 ). Следовательно,
). Следовательно,  .
.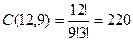 . Это число составляет значение
. Это число составляет значение  . Оставшиеся шесть места заполняются не отличниками (возможных кандидатов - 7). Общее число вариантов выбора равно
. Оставшиеся шесть места заполняются не отличниками (возможных кандидатов - 7). Общее число вариантов выбора равно  . Используя правило произведения, получим
. Используя правило произведения, получим 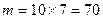 . Тогда,
. Тогда,  .
. Условной вероятностью события A при условии, что произошло событие B, называется величина
Условной вероятностью события A при условии, что произошло событие B, называется величина 
 . Событию
. Событию  . Поэтому,
. Поэтому,  .
.
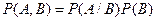 . В общем виде, предыдущее соотношение выглядит следующим образом:
. В общем виде, предыдущее соотношение выглядит следующим образом:
 . Тогда
. Тогда
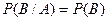 . Независимость одного события от другого означает, что осуществление одного из них никак не влияет на результат другого события.
. Независимость одного события от другого означает, что осуществление одного из них никак не влияет на результат другого события. и
и 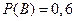 вероятность
вероятность  их совместного попадания равна
их совместного попадания равна  .
. и
и 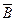 ,
,  называются попарно независимыми, если любая пара из них является парой независимых событий
называются попарно независимыми, если любая пара из них является парой независимых событий
 называются независимыми в совокупности, если вероятность одновременного осуществления любого конечного поднабора из них равна произведению вероятностей событий этого поднабора.
называются независимыми в совокупности, если вероятность одновременного осуществления любого конечного поднабора из них равна произведению вероятностей событий этого поднабора. , то из соотношения
, то из соотношения  ,
,  ,
, 

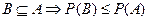


 - попал первый стрелок, второй – промахнулся;
- попал первый стрелок, второй – промахнулся; - попал второй стрелок, первый – промахнулся;
- попал второй стрелок, первый – промахнулся;


 , имеем
, имеем
 Пусть имеется полная группа событий
Пусть имеется полная группа событий 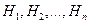 и для каждого из событий известна вероятность
и для каждого из событий известна вероятность  наступления этого события,
наступления этого события,  . Пусть А – некоторое событие, которое может наступить при выполнении одного из событий
. Пусть А – некоторое событие, которое может наступить при выполнении одного из событий  ,
,  . Необходимо найти
. Необходимо найти  .
. ; их объединение образует пространство элементарных исходов W. В этом случае событие
; их объединение образует пространство элементарных исходов W. В этом случае событие  :
:
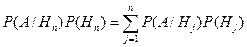
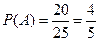 .
. - студент, сдававший первым, взял билет с вопросом, который наш студент не знает, и
- студент, сдававший первым, взял билет с вопросом, который наш студент не знает, и  - был взят билет с вопросом, который наш студент знает. Тогда
- был взят билет с вопросом, который наш студент знает. Тогда 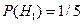 и
и  . Несложно подсчитать, что
. Несложно подсчитать, что 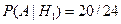 и
и  . По формуле полной вероятности получим
. По формуле полной вероятности получим [5]
[5] , которые образуют полную группу событий. Поскольку неизвестно какое из этих событий наступит, их называют гипотезами. Вероятность события
, которые образуют полную группу событий. Поскольку неизвестно какое из этих событий наступит, их называют гипотезами. Вероятность события 
 . Имеет место формула Байеса
. Имеет место формула Байеса
 , называются априорными (“a priori” – до опыта), вероятности
, называются априорными (“a priori” – до опыта), вероятности  вероятность наступления события
вероятность наступления события  . Если в результате опыта событие
. Если в результате опыта событие  , соответственно вторым лицом -
, соответственно вторым лицом -  . При проведении следственного эксперимента (событие
. При проведении следственного эксперимента (событие  ,
, 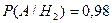 . По формуле Байеса
. По формуле Байеса
 :
: 
 :
:  ,
, образует распределение вероятностей с.в.
образует распределение вероятностей с.в.  , то
, то  .
. - вероятность появления герба при однократном подбрасывании монеты, через
- вероятность появления герба при однократном подбрасывании монеты, через  - вероятность выпадения
- вероятность выпадения 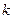 гербов при
гербов при  [8],
[8], 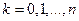 , где
, где  - число способов выбора
- число способов выбора  мы получаем распределение вероятностей из вышеприведенной таблицы.
мы получаем распределение вероятностей из вышеприведенной таблицы.
 , определенные на одном и том же пространстве элементарных событий, называются независимыми, если для любых значений а и b независимы события {X=a} и {Y=b}. Другими словами для любых значений а и b выполняется
, определенные на одном и том же пространстве элементарных событий, называются независимыми, если для любых значений а и b независимы события {X=a} и {Y=b}. Другими словами для любых значений а и b выполняется 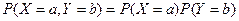 .
.
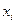 –
–  -е значение случайной величины, а
-е значение случайной величины, а 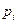 - вероятность принятия этого значения. Заметим, что если в формуле математического ожидания принять все вероятности равными 1/n, получается формула вычисления среднего арифметического чисел
- вероятность принятия этого значения. Заметим, что если в формуле математического ожидания принять все вероятности равными 1/n, получается формула вычисления среднего арифметического чисел  .
. .
.



