Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Одновыборочный критерий СтьюдентаСодержание книги
Поиск на нашем сайте
Задача 3.1. Имеются две выборки Требуется проверить гипотезу однородности выборок, которые, вообще говоря, являются зависимыми. Подтверждение гипотезы однородности означает, что эксперимент значимых результатов не дал. Один из возможных подходов к решению задачи сводится к проверке равенства нулю среднего значения разности двух выборок (одновыборочный критерий Стьюдента). Пусть имеются данные по 10 районам о количестве преступлений за 2006-2007 годы. Требуется определить, вызваны ли различия в показателях случайными факторами (данные взяты в разное время и естественно должны различаться) или изменения носят качественный характер. Исходные данные:
Непосредственный анализ данных в таблице показывает, что имеется тенденция к уменьшению числа преступлений. Нас интересует вопрос, действительно ли уменьшилось количество преступлений за приведенные годы и носит ли это изменение качественный характер. Поскольку каждое значение
Порядок вычислений 1. Ввести данные в столбцы A (наименование района), B (данные за 2006 год) и C(данные за 2007 год) 2. В ячейке D2 вычислить разности значений количества преступлений D2=B2-C2 за разные годы по району 1 3. Скопировать набранную формулу из ячейки D2 для каждого значения из столбца В 4. Вычислить среднее(СРЗНАЧ) для каждого из трех столбцов (B, C и D) (записать в ячейки G3,H3,I3) 5. для каждого из трех столбцов найти стандартные отклонения (функция СТАНДОТКЛОН) (записать в ячейки G4,H4,I4) 6. посчитать объемы выборок (функция СЧЕТ) (записать в ячейки G5,H5,I5) 7. используя найденные стандартные отклонения
(функция =I4/КОРЕНЬ(I5-1)) с помещением результата в ячейку I6 8. В ячейке G8 вычислить статистику Стьюдента =I3/I6
9. В ячейке G9 вычислить уровень значимости =СТЬЮДРАСП(G8,I5-1,1) (значение третьего аргумента функции СТЬЮДРАСП зависит от выбора альтернативной гипотезы. В нашем случае он равен 1, поскольку в качестве альтернативной гипотезы выбрана гипотеза «стало меньше» и рассматривается односторонняя критическая область) 10. По результатам анализа значения ячейки G9 (сравнения с критическим уровнем Результаты расчетов записать в следующую таблицу: F G H I
Задача 3.2. Ниже приведены сведения о мерах наказания, примененных в судах РТ за 1998-2001 гг.
Проверить значимо ли отличаются средние значения приведенных выборок за различные годы (по выбранным парам столбцов)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 346; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.61.88 (0.01 с.) |

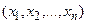 и
и 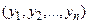 одинакового объема. Известно, что распределения выборок подчиняется нормальному закону, и, кроме того, измерения проводятся для одних и тех же объектов исследования в различное время или после проведения определенных действий(каждое значение
одинакового объема. Известно, что распределения выборок подчиняется нормальному закону, и, кроме того, измерения проводятся для одних и тех же объектов исследования в различное время или после проведения определенных действий(каждое значение  связано со значением
связано со значением 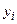 ). Примерами таких задач являются оценка эффективности применения нового лекарства (оцениваются показатели здоровья одних и тех же больных до и после лечения), сравнения уровня жизни населения при проведении социального эксперимента (сравниваются уровни жизни для фиксированной группы людей до и после эксперимента), влияния на студентов какого-либо вида учебной нагрузки (сравниваются показатели IQ для одной и той же группы студентов до и после чтения лекций). Конечно можно было бы провести соответствующие исследования для двух независимых однородных групп. Но даже без математических выкладок ясно, что результаты будут точнее, если исследуемая группа не меняется в ходе эксперимента.
). Примерами таких задач являются оценка эффективности применения нового лекарства (оцениваются показатели здоровья одних и тех же больных до и после лечения), сравнения уровня жизни населения при проведении социального эксперимента (сравниваются уровни жизни для фиксированной группы людей до и после эксперимента), влияния на студентов какого-либо вида учебной нагрузки (сравниваются показатели IQ для одной и той же группы студентов до и после чтения лекций). Конечно можно было бы провести соответствующие исследования для двух независимых однородных групп. Но даже без математических выкладок ясно, что результаты будут точнее, если исследуемая группа не меняется в ходе эксперимента. . Если с.в.
. Если с.в.  и
и 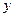 подчинены нормальному закону, то этому свойству удовлетворяет и их разность. В предположении, что обе выборки взяты из одной и той же генеральной совокупности следует, что математическое ожидание разности соответствующих значений равно нулю. В этом случае гипотеза однородности двух выборок может быть сформулирована в виде
подчинены нормальному закону, то этому свойству удовлетворяет и их разность. В предположении, что обе выборки взяты из одной и той же генеральной совокупности следует, что математическое ожидание разности соответствующих значений равно нулю. В этом случае гипотеза однородности двух выборок может быть сформулирована в виде 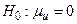 , где
, где 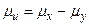 разность средних выборок
разность средних выборок  . Другой вариант альтернативной гипотезы
. Другой вариант альтернативной гипотезы 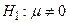 рассматривается в случае, когда необходимо просто проверить различие выборок. В качестве используемой статистики в задаче необходимо рассмотреть функцию
рассматривается в случае, когда необходимо просто проверить различие выборок. В качестве используемой статистики в задаче необходимо рассмотреть функцию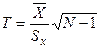 (статистика Стьюдента).
(статистика Стьюдента). и объем выборки вычислить стандартную ошибку среднего
и объем выборки вычислить стандартную ошибку среднего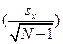
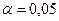 ) в ячейке G13 сделать вывод о предпочтении гипотезы или выбранной альтернативы
) в ячейке G13 сделать вывод о предпочтении гипотезы или выбранной альтернативы