
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерий согласия хи-квадратСодержание книги
Поиск на нашем сайте
Задача 3.6. Вернемся к задаче 2.1, которая состояла в построении гистограммы для вариационного ряда распределения значений роста. Гистограмма дает определенную информацию о функции плотности теоретического распределения. В частности, в задаче 2.1 визуально было выявлено, что функция плотности нормального распределения достаточно хорошо аппроксимирует построенную выборку. Однако визуальный подход не может считаться решением задачи. Рассмотрим критерий согласия 1. Выдвинуть гипотезу 2. Разбить область значений наблюдаемых данных на 3. По 4. Для каждого интервала вычислить теоретические вероятности 5. Вычислить статистику
представляющую меру расхождения между ожидаемыми (теоретическими) частотами 6. Задать уровень значимости 7. Принять решение о статистической значимости проверяемой гипотезы. Необходимо проверить гипотезу согласия
На основе построенной таблицы строится таблица группировки данных по интервалам и подсчитывается вспомогательная информация для проверки нулевой гипотезы(см. задание 2). Ниже приведен заголовок этой таблицы
Построение первых трех столбцов таблицы производится аналогично построениям, проводившимся при построении гистограммы с использованием функции =ЧАСТОТА(). При этом длина интервала, вообще говоря, зависит от выборочных данных. На практике число интервалов Задача 3.7. Проверить гипотезу о нормальности распределений для данных из задач 1.2 – 1.6.
Задание 4. Интервальные оценки При анализе выборочных данных можно вычислять выборочные характеристики, которые сами являются значениями случайных величин и могут изменяться в зависимости от выборки. Истинное значение соответствующей характеристики при этом остается неизвестным и не может быть, вообще говоря, точно определено. Поэтому для выборки заданного (особенно небольшого) объема весьма важным является описание интервала, в котором с разной степенью надежности находится неизвестное нам значение. Соответствующие оценки называются интервальными, а построенный интервал называется доверительным. Для построения доверительного интервала необходимо выполнение ряда условий о принадлежности распределения к определенному классу. Ниже рассматривается достаточно часто встречающаяся задача о построении доверительного интервала для среднего значения неизвестной случайной величины в предположении, что эта случайная величина распределена по нормальному закону. При этом исследователь должен заранее зафиксировать вероятность Построение
Задача 4.1. Имеется выборка
Необходимо выполнить следующие действия: 1. По выборочным данным находится среднее 2. Вычисляется стандартная ошибка среднего
где 3. Находится квантиль 4. Строятся доверительные границы Результаты вычислений оформить в виде следующей таблицы
Найти 95% ( Изменить значение
Задача 4.2. Построить 95%(второй вариант - 90%) доверительные интервалы для задач 1.1-1.6 задания 1. Задание 5. Исследование статистической зависимости между двумя характеристиками
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 335; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.211.58 (0.01 с.) |

 (хи-квадрат) выборочных данных с гипотезой о типе распределения. Этот критерий основан на сравнении эмпирических частот интервалов группировки с теоретическими (ожидаемыми) частотами, рассчитываемыми по формулам нормального распределения. Нулевая гипотеза для этой задачи записывается в форме
(хи-квадрат) выборочных данных с гипотезой о типе распределения. Этот критерий основан на сравнении эмпирических частот интервалов группировки с теоретическими (ожидаемыми) частотами, рассчитываемыми по формулам нормального распределения. Нулевая гипотеза для этой задачи записывается в форме  , где
, где 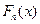 - эмпирическая функция распределения, построенная по имеющимся данным, а
- эмпирическая функция распределения, построенная по имеющимся данным, а 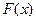 - гипотетическая (теоретическая) функция распределения с которой и сравнивается эмпирическая функция. Критерий согласия
- гипотетическая (теоретическая) функция распределения с которой и сравнивается эмпирическая функция. Критерий согласия 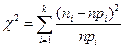 , где
, где 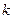 - число интервалов,
- число интервалов, 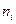 - количество значений выборки, попавшей в
- количество значений выборки, попавшей в 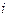 -й интервал,
-й интервал, 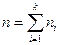 - объем выборки,
- объем выборки,  - теоретическая вероятность попадания изучаемой с.в. в
- теоретическая вероятность попадания изучаемой с.в. в 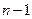 степенями свободы. Если при выбранном уровне значимости
степенями свободы. Если при выбранном уровне значимости  выполняется
выполняется 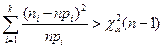 , то на уровне значимости
, то на уровне значимости 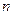 выборочным данным построить таблицу частот аналогично тому, как это делалось при построении гистограммы выборки.
выборочным данным построить таблицу частот аналогично тому, как это делалось при построении гистограммы выборки.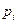 попадания значения с.в. в этот интервал.
попадания значения с.в. в этот интервал.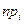 и выборочными частотами
и выборочными частотами 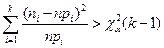

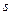




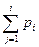
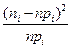
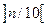 и
и  . Для задачи 1.1. значение
. Для задачи 1.1. значение  ) для каждого значения
) для каждого значения 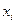 границы интервала. В результате столбец «теоретическая функция распределения» должен заполниться неубывающей последовательностью чисел (вероятностей)
границы интервала. В результате столбец «теоретическая функция распределения» должен заполниться неубывающей последовательностью чисел (вероятностей) 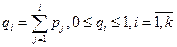 , где
, где 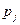 - теоретическая вероятность попадания в интервал с номером
- теоретическая вероятность попадания в интервал с номером  . Столбец «Ожидаемые частоты попадания значения с.в. в интервал» вычисляется по формуле
. Столбец «Ожидаемые частоты попадания значения с.в. в интервал» вычисляется по формуле  , где
, где 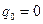 . Для
. Для 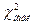 . Далее это значение необходимо сравнить со значением функции
. Далее это значение необходимо сравнить со значением функции  =ХИ2ОБР(уровень значимости,
=ХИ2ОБР(уровень значимости, 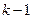 )[15] и принять решение о статистической значимости проверяемой гипотезы. Если
)[15] и принять решение о статистической значимости проверяемой гипотезы. Если 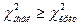 , то эмпирическое распределение не соответствует нормальному распределению на выбранном уровне значимости, в противном случае нет оснований отрицать это соответствие.
, то эмпирическое распределение не соответствует нормальному распределению на выбранном уровне значимости, в противном случае нет оснований отрицать это соответствие.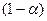 доверительного интервала для среднего
доверительного интервала для среднего  предполагает нахождение границ
предполагает нахождение границ  и
и 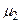 , которые удовлетворяют неравенству
, которые удовлетворяют неравенству 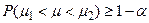 . Указанная формула означает, что интервал
. Указанная формула означает, что интервал 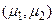 с вероятностью
с вероятностью 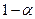 накроет неизвестное значение
накроет неизвестное значение 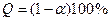 называется надежностью интервала и выбирается обычно в пределах от 90% до 99%, причем, чем больше величина
называется надежностью интервала и выбирается обычно в пределах от 90% до 99%, причем, чем больше величина 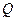 , тем шире получается доверительный интервал и хуже точность оценки. Задача построения доверительного интервала с заданной точностью и надежностью может быть решена только при достаточно большом объеме выборки.
, тем шире получается доверительный интервал и хуже точность оценки. Задача построения доверительного интервала с заданной точностью и надежностью может быть решена только при достаточно большом объеме выборки. из нормального распределения. Необходимо построить 95% доверительный интервал (верхнюю и нижнюю границы) для неизвестного среднего
из нормального распределения. Необходимо построить 95% доверительный интервал (верхнюю и нижнюю границы) для неизвестного среднего 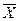 и выборочная дисперсия
и выборочная дисперсия 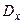
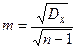 ,
, распределения Стьюдента
распределения Стьюдента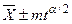
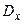
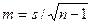
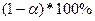
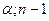
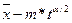
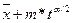
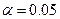 ) доверительный интервал для задачи 4.1.
) доверительный интервал для задачи 4.1.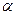 в большую сторону (
в большую сторону (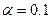 ) и в меньшую сторону (
) и в меньшую сторону (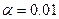 ) и проанализировать, как изменяются границы доверительного интервала для заданного уровня надежности.
) и проанализировать, как изменяются границы доверительного интервала для заданного уровня надежности.


