
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Автокорреляция в динамических рядах. Авторегрессионные модели.Содержание книги
Поиск на нашем сайте
Еще одним подходом к описанию основной тенденции временного ряда и прогнозированию является авторегрессионная модель. Ее построению предшествует оценка наличия автокорреляции в изучаемом ряду. При анализе динамических рядов особый интерес представляет оценка степени зависимости изменений в уровнях одного ряда от изменений, происходящих в уровнях другого ряда Вторая особенность состоит в том, что одним из основных условий применения методов корреляции является независимость отдельных наблюдений. Автокорреляция – это зависимость между последовательными значениями (уровнями) временного ряда. Автокорреляция первого порядка (first-order autocorrelation) оценивает степень зависимости между соседними значениями временного ряда. Автокорреляция второго порядка (second-order autocorrelation) оценивает тесноту связи между значениями, разделенными двумя временными интервалами, и т.д. Интервал времени, разделяющий зависимые уровни динамического ряда, называется лагом (lag). Автокорреляционная зависимость может быть представлена как зависимость между уровнями исходного ряда:
у1, у2, у3, …, уn
и того же ряда, но смещенного на i периодов (моментов) времени:
Интервал смещения (i) - временной лаг (i = 1, i = 2, i = 3 и т. д.). Если при изучении отдельных динамических рядов наличие автокорреляции помогало выявлению тенденции развития явления, то при анализе корреляционной зависимости между рядами ее следует исключить. Наличие автокорреляции проверяется на основе коэффициентов автокорреляции. При этом в качестве результативного признака принимается переменная, содержащая фактические значения уровней исходного ряда динамики, а в качестве факторного признака переменная, содержащая фактические уровни смещенного ряда. Величина временного лага определяет порядок коэффициента автокорреляции. Математической статистикой разработаны циклический и нециклический коэффициент автокорреляции. На практике чаще используется нециклический коэффициент автокорреляции, который может быть рассчитан по формуле:
Если динамический ряд У(t) достаточно большой, а i = 1, то дисперсии рядов У(t), У(t-i), а также их средние уровни практически равны. Поэтому формулу можно записать следующим образом:
Для проверки нулевой гипотезы об отсутствии автокорреляции фактическая величина коэффициента сопоставляется с табличным значением для соответствующего уровня значимости. Поскольку таблицы содержат критические значения коэффициента автокорреляции, то нулевая гипотеза может быть принята, если фактическое значение коэффициента меньше табличного.Когда фактическая величина коэффициента превышает табличное значение, нулевая гипотеза отвегается и признается наличие автокорреляции в исследуемом ряду. Вычисление коэффициентов автокорреляции в динамических рядах в системе STATISTICA осуществляется аналогично рассмотренному ранее случаю с определением коэффициента автокорреляции в остатках тренда.
Рис. 106. Коэффициенты автокорреляции для импорта в 3 периоде
Рис. 107. График автокоррелляций переменной «Import» в 3 периоде
Рис. 108. Коэффициенты автокорреляции для экспорта в 3 периоде
Рис. 109. График автокоррелляций переменной «Export» в 3 периоде
Напомним, что в STATISTICA красным цветом высвечиваются статистически значимые оценки. Следовательно, можно сделать вывод об отсутствии автокорреляции в изучаемом динамическом ряду.
Поскольку в нашем примере отсутствует автокорреляция, построим авторегрессионную модель в методических целях, сместив исходный ряд на 1 лаг, т.е. модель первого порядка. Для вычисления параметров уравнения авторегрессии потребуется создать дополнительную переменную Длина переменных должна быть одинаковой, для чего нужно удалить в первом столбце последнюю и во втором - первую строки. Процедура расчета численных значений коэффициентов уравнения авторегрессии идентична определению параметров уравнений для различных трендовых моделей и осуществляется с помощью меню Statistics/Multiple Regression. При этом в качестве зависимой переменной выбирается исходный ряд, в качестве независимой – ряд сдвинутый на лаг назад, так как нас интересует зависимость текущего уровня от предыдущего.
Рис. 110. Данные регрессионного анализа (импорт)
Рис. 111. Данные регрессионного анализа (экспорт) Соответственно, уравнения авторегрессии имеют вид:
Как правило, авторегрессионная модель позволяет лучше, чем трендовая, описать предысторию процесса и получить более точный прогноз. Но для этого необходимо, чтобы уравнение и все его параметры были статистически значимы. На основе данного уравнения сделаем прогноз на объем экспорта и импорта за 2006 года.
Графики авторегрессий для экспорта и импорта Японии выглядят следующим образом:
Рис. 112. Авторегрессия для импорта в третьем периоде
Рис. 113. Авторегрессия для экспорта в третьем периоде
Корреляция рядов динамики
При изучении тенденции развития явления во времени часто возникает необходимость определить степень зависимости между динамическими рядами. Корреляционная связь между уровнями двух динамических рядов называется кросс-корреляцией. Оценка тесноты связи в задачах исследования кросс-корреляции производится с использованием стандартного коэффициента корреляции Пирсона. Однако применение традиционных методов корреляции и регрессии к анализу зависимости временных рядов имеет определенные особенности. Особое значение приобретает теоретический, содержательный анализ изучаемых явлений и их возможных взаимосвязей во избежание оценки «ложной корреляции». Если в двух рядахнаблюдается однонаправленная тенденция изменения уровней, то между ними будет отмечаться положительная ковариация:
смешанный корреляционный момент первой степени. Величина коэффициента корреляции, который представляет собой нормированный показатель ковариации, в этих условиях может оказаться достаточно большой. Однако однонаправленность трендов и высокое значение коэффициента корреляции вовсе не означает наличие причинно-следственной зависимости между рядами. Поэтому, прежде чем приступать к количественной оценке корреляционной зависимости, необходимо теоретически обосновать ее наличие. Вторая особенность обусловлена тем, что одним из условий применения КРА является независимость наблюдений. В контексте изучения временных рядов – это отсутствие связи между уровнями ряда, т.е. автокорреляции. Наличие тренда (автокорреляции) в анализируемых динамических рядах может существенно исказить оценку. Поэтому для получения адекватного результата, необходимо предварительно исключить тенденцию из анализируемых рядов. Существует несколько способов исключения автокорреляции (тенденции). Один из них основан на переходе от корреляции уровней ряда к корреляции остатков, отклонений фактических уровней от тренда. При этом: - определяют форму тренда и производят аналитическое выравнивание каждого из связных рядов; - рассчитывают отклонения фактических уровней от соответствующих выровненных уровней по каждому ряду; - определяют численное значение коэффициента корреляции по полученным отклонениям. Если обозначить отклонение от тренда по ряду, содержащему результативный признак –
В том случае, когда тенденция описывается уравнениями прямой или параболы, среднее отклонение от тренда всегда равно нулю. Для других типов тренда это равенство выполняется, если математическая функция достаточно точно отражает фактическую тенденцию. Если
Зная коэффициент корреляции, можно определить коэффициент регрессии, который для линейной зависимости будет определяться:
Свободный член уравнения в данном случае будет равен нулю, поскольку:
Таким образом, уравнение регрессии отклонений от тренда примет вид:
Практика показывает, что часто в отклонениях от тренда сохраняется автокорреляция. Прежде чем приступить к расчету коэффициента корреляции по остаткам, необходимо проверить наличие в них автокорреляции. Наряду с коррелированием остатков, способом обойти автокорреляцию уровней может быть метод коррелирования последовательныхразностей или тех цепных показателей динамических рядов, которые являются константами их трендов. Так, для линейного тренда – это цепные абсолютные приросты (
Данный подход к исключению автокорреляции вполне оправдан. На длительном временном отрезке искажение корреляции при наличии тренда может быть весьма существенным, благодаря кумулятивному эффекту. В разностях между соседними уровнями воздействие тренда незначительно, т. к. в большей мере они отображают влияние колеблемости. Если установлено, что тенденция ряда близка к экспоненте, рекомендуется коррелировать цепные темпы роста. При наличии в анализируемых рядах тенденций разного типа, допускается коррелирование разных цепных показателей, являющихся константами различных трендов. Еще один прием устранения автокорреляции основан на включении времени в уравнение регрессиив качестве аргумента:
Математически доказано, что непосредственное введение в уравнение регрессии фактора времени устраняет автокорреляцию, аналогично использованию отклонений фактических уровней от тренда. Это свойство, доказанное в теореме Фриша справедливо не только для линейной тенденции. Простота реализации этого подхода явилась причиной его широкого применения в практических исследованиях. При изучении связи между временными рядами следует помнить, что между изменением уровней одного ряда, как отклика на изменение уровней другого, может существовать определенный временной лаг. Коэффициенты кросс-корреляции на основе отклонений от трендов в STATISTICA рассчитываются точно так же, как и коэффициенты автокорреляции. Только на закладке Autocorrelations выбирается кнопка Crosscorrelations. Напомним, что это осуществляется с помощью меню Statistics/Advanced Linear/Nonlinear Models/Time Series Forecasting. И выбрать необходимо сразу две переменные: отклонения от лучших трендов одного и второго динамических рядов.
Рис. 114. Параметры кросс-корреляции
На основании рассчитанных коэффициентов кросс-корреляции определяется лаг наиболее существенной взаимосвязи между динамическими рядами, то есть тот лаг, которому соответствует максимальный коэффициент кросс-корреляции (помечается красным цветом). В нашем случае максимально значение достигается при Это свидетельствует о статистически значимой тесноте связи между двумя динамическими рядами при Описанный выше прием непосредственного включения в уравнение связи фактора времени, позволяет не только оценить зависимость между рядами, но и получить модель для прогнозирования.
где i - лаг наибольшей взаимосвязи между рядами, в нашем случае В демонстрационном примере невозможно теоретически обосновать, какой из динамических рядов является признаком-фактором, а кокой признаком-результатом, т.е. обосновать причинно-следственную связь. Поэтому построим два уравнения, в которых в качестве результативной переменной будут выступать разные динамические ряды. Расчет параметров этих факторно-временных функций осуществляется аналогично коэффициентам любого другого уравнения регрессии в меню Statistics/Multiple Regression. При построении уравнений в поле зависимых и независимых переменных меняем динамические ряды местами и добавляем переменную Т - время.
Рис. 116. Параметры факторно-временных функций
Рис. 117. Параметры факторно-временных функций
Для прогнозирования следует выбрать уравнение на основе максимального коэффициента детерминации из таблиц Regression Summary (или использовать другие критерии). При условии статистической значимости уравнения и параметров модель может быть использована для прогнозирования. Максимальный коэффициент детерминации в 1 таблице.. В нашем случае мы используем уравнение, где признаком-результатом является третий период импорта, а признаком-фактором третий период экспорта и фактор времени:
где
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1391; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.184.27 (0.009 с.) |

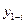 , у2-i, у3-i, …, уn-i.
, у2-i, у3-i, …, уn-i.




 . Воспользуемся тем же приемом, что и при расчете показателей изменения уровней динамического ряда. Выберем меню Statistics/Advanced Linear/Nonlinear Models/Times Series/Forecasting, в качестве переменной используем исходные данные третьего периода. Нажимаем кнопку ОК, переходим на закладку Shift и в поле Shift (Lag) Series Back ставим 1. Далее нажимаем ОК (Transform selected series) и сохраняем полученные данные с помощью кнопки Save variables. В результате получаем таблицу с двумя переменными, первая - исходный ряд, а вторая – ряд, смещенный на 1 период.
. Воспользуемся тем же приемом, что и при расчете показателей изменения уровней динамического ряда. Выберем меню Statistics/Advanced Linear/Nonlinear Models/Times Series/Forecasting, в качестве переменной используем исходные данные третьего периода. Нажимаем кнопку ОК, переходим на закладку Shift и в поле Shift (Lag) Series Back ставим 1. Далее нажимаем ОК (Transform selected series) и сохраняем полученные данные с помощью кнопки Save variables. В результате получаем таблицу с двумя переменными, первая - исходный ряд, а вторая – ряд, смещенный на 1 период.

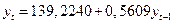 для импорта,
для импорта, для экспорта.
для экспорта.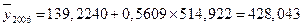 млрд. $ US составил объем импорта,
млрд. $ US составил объем импорта, млрд. $ US составил объем экспорта.
млрд. $ US составил объем экспорта.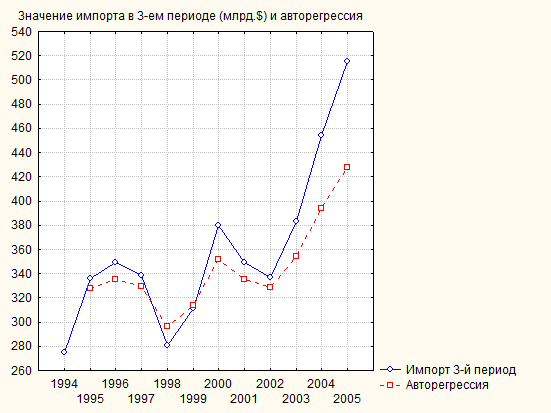

 –
– , а по ряду, содержащему факторный признак -
, а по ряду, содержащему факторный признак -  , то коэффициент корреляции можно рассчитать по следующей формуле:
, то коэффициент корреляции можно рассчитать по следующей формуле:
 , формула принимает вид:
, формула принимает вид:

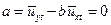

 и
и  ), а коэффициент корреляции будет определяться по формуле:
), а коэффициент корреляции будет определяться по формуле:
 .
.
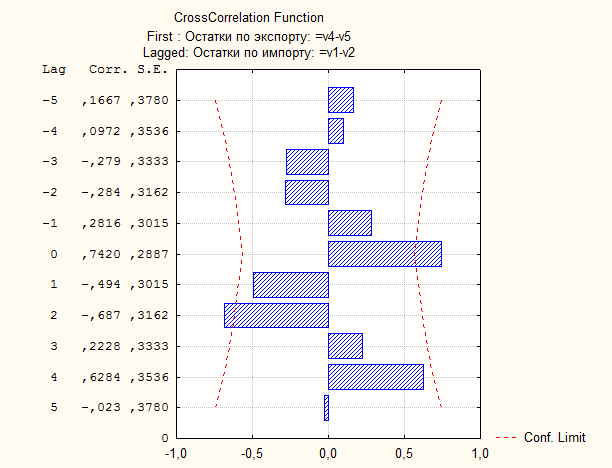 РРис. 115. График кросс-коррелляций переменных «остатки по экспорту» и «остатки по импорту»
РРис. 115. График кросс-коррелляций переменных «остатки по экспорту» и «остатки по импорту» и составляет r = 0,742002.
и составляет r = 0,742002. ,
,


 - значение уровня динамического ряда, рассчитанное по линейной модели авторегрессии первого порядка для экспорта Японии в 2006 году, поэтому кросс-корреляционная модель прогноза получится очень далекой от реальной тенденции. Так как фактических данных при прогнозировании не имеем. Рассчитаем
- значение уровня динамического ряда, рассчитанное по линейной модели авторегрессии первого порядка для экспорта Японии в 2006 году, поэтому кросс-корреляционная модель прогноза получится очень далекой от реальной тенденции. Так как фактических данных при прогнозировании не имеем. Рассчитаем 




