
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выравнивание по скользящей среднейСодержание книги
Поиск на нашем сайте
Один из наиболее простых приемов сглаживания заключается в расчете скользящих, или, как иногда их называют, подвижных средних. Применение последних, позволяет сгладить периодические и случайные колебания и тем самым выявить присутствующую в развитии тенденцию. Пусть динамический ряд состоит из уровней yt, t = 1,..., n. Для каждых m последовательных уровней этого ряда (т < n) можно подсчитать среднюю величину. Вычислив значение средней для первых т уровней, переходят к расчету средней для уровней y 2 ,..., yт+i, затем y 3,..., ym +2 и т. д. Таким образом, интервал сглаживания, т. е. интервал, для которого подсчитывается средняя, как бы скользит по динамическому ряду с шагом, равным единице. Если т нечетное число, а предпочтительнее брать именно нечетное число уровней, поскольку в этом случае расчетное значение уровня окажется в центре интервала сглаживания и им легко заменить конкретное фактическое значение, то для определения скользящей средней можно записать следующую формулу:
где yi - фактическое значение уровня в момент i; i - порядковый номер уровня в интервале сглаживания; m - интервал сглаживания (период скольжения). Величина р легко определяется из продолжительности интервала сглаживания. Поскольку т = 2р + 1 при нечетном т, то
Расчет скользящей средней при большом числе уровней можно несколько упростить, применив ряд приемов. Так, последовательные значения скользящей средней можно определить рекурсивно:
или путем последовательного расчета накопленных сумм уровней. Обозначим кумулятивную сумму уровней от начала ряда до уровня j включительно как uj; u 1 =y 1; u 2 =u 1 +y 2; u 3 =u 2 +y 3и т. д. Тогда числитель формулы (2.4) можно записать как ut+p - ut-p- 1, соответственно:
Выбор периода скольжения имеет большое значение, особенно, если в изучаемом ряду имеются циклические колебания. В этом случае период скольжения должен быть равным, либо кратным периоду колеблемости. Если циклических колебаний не наблюдается, то рекомендуется выполнить несколько вариантов выравнивания: начать с расчета скользящей средней с минимальным периодом скольжения и постепенно увеличивать период сглаживания, пока основная тенденция не проявится достаточно отчетливо. Средние, рассчитанные по большому периоду, лучше сглаживают случайные колебание. Но использование многочленных скользящих средних может быть ограничено незначительной продолжительностью исходного ряда. Необходимо учитывать, что использование метода скользящих средних приводит к получению укороченного временного ряда.
Для выбора лучшего варианта выравнивания по скользящей средней может быть использован формальный критерий, основанный на сравнении сумм квадратов отклонений фактических уровней ряда от значений уровней выровненного ряда.
где
Очевидно, что если тенденция в результате сглаживания проявляется достаточно четко, то чем меньше В рамках курсового проекта требуется провести сглаживание динамического ряда 3-х и 5-ти членными скользящими средними.
Для начала работы воспользуемся уже известным нам меню Statistics/Advanced Linear/Nonlinear Models/Time Series/Forecasting. В появившемся окне указываем переменную, с которой будем работать (Import, Export), нажимаем на кнопку ОК (transformations, autocorrelations, crosscorrelations, plots) и затем выбираем закладку Smoothing.
Рис. 33. Вкладка меню Time Series/Forecasting На данной закладке мы выбираем опцию N-точечной скользящей средней N-pts Moving Average. Для получения 3-х членной скользящей средней в поле интервала сглаживания N мы ставим цифру 3 (N = 3), а для 5-ти членной – соответственно, цифру 5. Далее нажимаем на кнопку ОК (Transform selected series), система автоматически строит тренд, выраженный скользящей средней с заданными параметрами, а в информационное поле добавляются соответствующие переменные, которые необходимо сохранить с помощью кнопки Save variables (как это было сделано при расчете показателей изменения уровней динамического ряда). Далее переносим сохраненные значения в нашу рабочую книгу (кнопка Add to Workbook), переименовываем их удобным образом и строим графики с помощью уже известной процедуры Graphs/2D Graphs/Line Plots (Variables). На одном графике целесообразно представить исходный динамический ряд и ряд, полученный в результате выравнивания по одной из скользящих средних.
Рис. 34. Сглаживание динамического ряда Import 3-х членной скользящей средней
Рис. 35. Сглаживание динамического ряда Export 3-х членной скользящей средней
Рис. 36. Сглаживание динамического ряда Import 5-ти членной скользящей средней
Рис. 37. Сглаживание динамического ряда Export 5-ти членной скользящей средней
На представленных графиках отчетливо видно, что выравнивание с периодом скольжения пять лет, дает лучшие результаты. Простые скользящие средние — относительно грубый статистический прием выявления тенденции. В ряде случаев сглаживание с помощью простой скользящей средней оказывается настолько сильным, что тенденция развития проявляется лишь в самом общем виде, а отдельные важные для экономического анализа детали теряются. Часто после сглаживания мелкие волны или вообще исчезают, или меняют свой знак, т. е. вместо выпуклого участка на кривой получают вогнутый, и наоборот.
|
||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 677; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.116.231 (0.01 с.) |

 ,
, -значение скользящей средней для момента t,
-значение скользящей средней для момента t, .
.
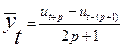
 ,
, ¾ значения уровней исходного ряда;
¾ значения уровней исходного ряда;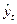 ¾ значения уровней выровненного ряда;
¾ значения уровней выровненного ряда; ¾ число выровненных уровней.
¾ число выровненных уровней. , тем лучше выравнивание.
, тем лучше выравнивание.







