
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Экстраполяция трендов и доверительные интервалы прогнозаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Один из наиболее распространенных методов прогнозирования заключается в экстраполяции, т.е. в продлении в будущее тенденции, наблюдавшейся в прошлом. Экстраполяция тенденций динамических рядов сравнительно широко применяется в практических исследованиях в силу ее простоты, возможности осуществления на основе относительно небольшого объема информации, наконец, ясности принимаемых допущений. Отсутствие иной информации помимо отдельно рассматриваемого динамического ряда часто оказывается решающим аргументом при выборе этого метода прогнозирования. При таком подходе к прогнозированию предполагается, что размер признака, характеризующего явление, формируется под воздействием множества факторов, причем не представляется возможным выделить порознь их влияние. В связи с этим ход развития связывается не с какими-либо конкретными факторами, а с течением времени. Экстраполяция базируется на следующих допущениях: 1) развитие явления может быть с достаточным основанием охарактеризовано плавной (эволюторной) траекторией — трендом; 2) общие условия, определяющие тенденцию развития в прошлом, не претерпят существенных изменений в будущем. Таким образом, экстраполяция дает описание некоторого общего будущего развития объекта прогнозирования. Причем если развитие в прошлом носило перманентно скачкообразный характер, то при достаточно продолжительном периоде наблюдений скачки оказываются “зафиксированными” в самом тренде, и последний опять-таки можно применить в прогнозировании. Выше были сформулированы основные условия, наличие которых дает возможность осуществлять экстраполяцию тренда. В практике прогнозирования может возникнуть вопрос, а как поступить, если условия формирования тренда заметно изменяются и этого следует ожидать и в будущем? В этом случае возможны различные подходы к решению проблем. В частности, в ряде случаев тренд можно “исправить”, сокращая период наблюдения, отсекая члены ряда, сформировавшиеся при явно других условиях и искажающие новую тенденцию. Однако далеко не всегда можно провести четкую границу во времени, разделяющую новые и старые условия развития исследуемого явления. В этом случае подходящим является оценивание параметров, учитывающее устаревание данных. Такой прием возможен тогда, когда переход к новым условиям не имеет резкой границы и в то же время есть, основания считать влияние этого перехода достаточно эффективным. Наконец, возможна корректировка параметров уравнений, характеризующих тренд. Например, изменение постоянного члена в уравнении полинома сдвигает тренд по оси ординат, не изменяя формы кривой. Такой прием применим, когда предполагается, что развитие будет следовать прошлой тенденции, однако есть основание для перехода к какому-либо базовому уровню, отличающемуся от уровня, полученного по уравнению тренда. Корректированию могут быть подвергнуты и другие параметры (помимо постоянного члена). Такого рода поправки изменяют форму тренда. Например, изменяют угол наклона прямой, растягивают или сжимают кривую и т.д. Подобные деформации тренда, разумеется, должны иметь достаточные основания. По-видимому, самым правильным было бы рассматривать экстраполяцию не как конечный результат прогнозирования, а как некоторый отправной момент, на основе которого с привлечением дополнительной информации, не содержащейся в самом динамическом ряду, разрабатывают прогноз. Вместе с тем часто ее результат с соответствующей корректировкой или без нее рассматривается и как окончательный прогноз. Если при анализе развития объекта прогноза есть основания принять два базовых допущения экстраполяции, о которых говорилось выше, то процесс прогнозирования заключается в подстановке соответствующей величины периода упреждения в формулу, описывающую тренд. Проведем прогнозирование на основе экстраполяции лучшей формы тренда (полином 3-ей степени) для третьего периода исходного динамического ряда:
Соответственно прогноз объем экспорта и импорта на 2006 год (t=13) составит: Экспорт: Импорт: Соответственно прогноз объем экспорта и импорта на 2007 год (t=14) составит: Экспорт: Импорт: Экстраполяция дает возможность получить точечное значение прогноза, что может быть признано удовлетворительным только при наличии функциональной зависимости. Однако для экономических явлений характерна корреляционная зависимость и переменные, как правило, являются непрерывными. Следовательно, указание точечных значений прогноза, строго говоря, лишено содержания, поскольку “попадание” в точку имеет нулевую вероятность. Отсюда следует, что прогноз должен быть дан в виде интервала значений, т.е. необходимо определение доверительного интервала прогноза. 6.1. Доверительные интервалы прогноза При определении прогностических значений того или иного явления с помощью экстраполяции наибольший интерес представляет, по-видимому, не сама экстраполяция — это более или менее механический прием, а определение доверительных интервалов прогноза. Доверительные интервалы могут быть определены двояко: формально и неформально. Что касается последнего, то это дело экспертного суждения, которое выносится при качественном осмыслении результатов прогноза, сопоставлении их с другими имеющимися у эксперта данными. При этом, естественно, эксперт должен учитывать не только степень колеблемости фактических уровней вокруг тренда в прошлом, но и возможность деформации тренда в будущем (соответственно могут быть получены различные варианты прогноза). Формальный доверительный интервал учитывает лишь ту неопределенность, которая связана с ограниченностью числа наблюдений и соответствующей неточностью найденных оценок параметров кривой. Основной вопрос - в какой мере в будущем сохранится найденная тенденция, — естественно, не может быть решен с помощью таких доверительных интервалов. Это дело содержательного экономического анализа и экспертной оценки. Основное внимание в данном учебном пособии уделим оценке формальных доверительных интервалов, базирующихся на статистическом анализе. Заметим, что формальные доверительные интервалы можно получить далеко не во всех случаях. В частности, для сложных кривых, отличающихся от полиномов, если их и можно определить, доверительные интервалы имеют достаточно условный характер.Как было сказано выше, точное совпадение фактических данных и прогностических точечных оценок, полученных путем экстраполяции кривых, характеризующих тенденцию, — явление маловероятное. Соответствующая погрешность имеет следующие источники: 1) выбор формы кривой, характеризующей тренд, содержит элемент субъективизма. Во всяком случае, часто нет твердой основы для того, чтобы утверждать, что выбранная форма кривой является единственно возможной, а тем более лучшей для экстраполяции в данных конкретных условиях; 2) оценивание параметров кривых (иначе говоря, оценивание тренда) производится на основе ограниченной совокупности наблюдений, каждое из которых содержит случайную компоненту. В силу этого параметрам кривой, а, следовательно, и ее положению в пространстве свойственна некоторая неопределенность; 3) тренд характеризует средний уровень ряда на каждый момент времени. Отдельные наблюдения, как правило, отклонялись от него в прошлом. Естественно ожидать, что подобного рода отклонения будут происходить и в будущем. Вполне возможны случаи, когда форма кривой, описывающей тенденцию, выбрана неправильно или когда тенденция развития в будущем может существенно измениться и не следовать тому типу кривой, который был принят при выравнивании. В последнем случае основное допущение экстраполяции не соответствует фактическому положению вещей. Найденная кривая лишь выравнивает динамический ряд и характеризует тенденцию только в пределах периода, охваченного наблюдением. Экстраполяция такого тренда неизбежно приведет к ошибочному результату, причем ошибку такого рода нельзя оценить заранее. В связи с этим можно лишь отметить то, что, по-видимому, следует ожидать рост такой погрешности (или вероятности ее возникновения) при увеличении периода упреждения. Погрешность, связанная со вторым и третьим источниками, может быть отражена в виде доверительного интервала прогноза при принятии некоторых допущений о свойстве ряда. С помощью такого интервала точечный прогноз преобразуется в интервальный. Интуитивно понятно, что в основу расчета доверительного интервала прогноза должен быть положен измеритель колеблемости ряда наблюдаемых значений признака. Чем выше эта колеблемость, тем менее определенно положение тренда в пространстве “уровень — время” и тем шире должен быть интервал для вариантов прогноза при одной и той же степени доверия. Традиционно в качестве такого измерителя колеблемости используется среднее квадратическое (стандартное) отклонение фактических наблюдений от расчетных, полученных при выравнивании динамического ряда. В общем виде среднее квадратическое отклонение от тренда можно выразить как
где f ¾ число степеней свободы, f = n ‑ т, где т ¾ число оцениваемых параметров; n ¾ число наблюдений. Так, если выравнивание производится по прямой, то f = n ‑ 2, для параболы второй степени f = n ‑ 3 и т. д. Сумму квадратов отклонений от тренда (возьмем для простоты линейный тренд) можно, очевидно, разложить следующим образом:
Это выражение можно упростить. Допустим, что начало отсчета времени находится в середине ряда, тогда S t = 0. Параметры а и b, как мы уже убедились ранее, в этом случае равны:
Отсюда после упрощений получаем:
Разность первых двух членов правой стороны этого равенства равна сумме квадратов отклонений от средней арифметической, т. е.
Выражение показывает, что сумма квадратов отклонений от линейного тренда меньше, чем от средней арифметической. Этим выражением можно воспользоваться в тех случаях, когда характеристика колебаний вокруг тренда определяется до того, как определен сам тренд. Сумма квадратов отклонений от линий тренда, т. е. Прежде чем приступить к определению доверительного интервала прогноза, необходимо сделать оговорку о некоторой условности рассматриваемого ниже расчета. То, что следует далее, является, в некоторой мере, произвольным перенесением результатов, найденных для регрессии выборочных показателей, на анализ динамических рядов. Дело в том, что предположение регрессионного анализа о нормальности распределения отклонений вокруг линии регрессии не может, по существу, безоговорочно утверждаться при анализе динамических рядов. Полученные в ходе статистического оценивания параметры не свободны от погрешности, связанной с тем, что объем информации, на основе которой производилось оценивание, ограничен, и в некотором смысле эту информацию можно рассматривать как выборку. Во всяком случае, смещение периода наблюдения только на один шаг или добавление, или устранение членов ряда в силу того, что каждый член ряда содержит случайную компоненту, приводит к изменению численных оценок параметров. Отсюда расчетные значения В общем виде доверительный интервал для тренда определяется как:
где
Доверительный интервал для прогноза, очевидно, должен учитывать не только неопределенность, связанную с положением тренда, но возможность отклонения от этого тренда. В практике встречаются случаи, когда более или менее обоснованно для экстраполяции можно применить несколько типов кривых. При этом рассуждения иногда сводятся к следующему. Поскольку каждая из кривых характеризует один из альтернативных трендов, то очевидно, что пространство между экстраполируемыми трендами и представляет собой некоторую “естественную доверительную область” для прогнозируемой величины. С таким утверждением нельзя согласиться. Прежде всего потому, что каждая из возможных линий тренда отвечает некоторой заранее принятой гипотезе развития. Пространство же между трендами не связано ни с одной из них — через него можно провести неограниченное число трендов. Следует также добавить, что доверительный интервал связан с некоторым уровнем вероятности выхода за его границы. Пространство между трендами не связано ни с каким уровнем вероятности, а зависит от выбора типов кривых. К тому же при достаточно продолжительном периоде упреждения это пространство, как правило, становится настолько значительным, что подобный “доверительный интервал” теряет всякий смысл. В STATISTICA при расчете доверительных интервалов прогноза величину среднего квадратического отклонения Sy можно определить воспользовавшись таблицей дисперсионного анализа. Рассчитанное в ячейке Residual Mean Squares значение соответствует подкоренному выражению в формуле для Sy, то есть остаточной дисперсии.Остается только извлечь из него квадратный корень. Однако, необходимо помнить, о том, что мы пользовались линеаризацией, а соответственно этот показатель также необходимо пересчитать.
Рис. 118. Форма для расчета критерия Фишера (импорт)
Рис. 119. Форма для расчета критерия Фишера (экспорт)
Далее рассмотрим значения критерия Стьюдента t при доверительной вероятности 95%. При использовании полинома 3 степени число степеней свободы равно 9 (число периодов исходного ряда минус число параметров уравнения), соответственно значение критерия равно 2,306. Для уравнения авторегрессии значение критерия 2,262 (линейная модель), а при использовании факторно-временной функции (кросс-корреляция) число параметров уравнения равно 2, и, соответственно, значение критерия Стьюдента равно 2,228. Также необходимо отметить, что для уравнений авторегрессии и факторно-временной функции нет необходимости в пересчете остаточной дисперсии, так как это функции линейного вида. Соответственно приведем доверительные интервалы для прогнозного значения экспорта и импорта на 2006 год. 1. На основе уравнения тренда · Уравнение тренда для экспорта:
· Уравнение тренда для импорта:
2. На основе уравнения авторегрессии. · Уравнение авторегрессии для экспорта:
· Уравнение авторегрессии для импорта:
3. На основе уравнения кросс-корреляции. · Уравнение кросс-корреляции для экспорта:
· Уравнение кросс-корреляции для импорта:
Напомним, что фактическое значение объема экспорта составляет 649,931 млрд. $ US, импорта 579,574 млрд. $ US.
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1369; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.164.100 (0.013 с.) |

 для экспорта,
для экспорта, для импорта.
для импорта. млрд.$ US,
млрд.$ US, млрд.$US.
млрд.$US. млрд.$ US,
млрд.$ US, млрд.$US.
млрд.$US. ,
,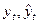 ¾соответственно фактическое и расчетное значения уровня ряда;
¾соответственно фактическое и расчетное значения уровня ряда;


 . Таким образом,
. Таким образом,
 , и среднее квадратическое отклонение от тренда Sy являются основой при определении средней квадратической ошибки отдельных параметров уравнения тренда и их доверительных интервалов, а также ошибки и доверительных интервалов тренда и прогноза.
, и среднее квадратическое отклонение от тренда Sy являются основой при определении средней квадратической ошибки отдельных параметров уравнения тренда и их доверительных интервалов, а также ошибки и доверительных интервалов тренда и прогноза. несут на себе груз неопределенности, связанной с ошибками в значении параметров.
несут на себе груз неопределенности, связанной с ошибками в значении параметров. ,
, ¾ средняя квадратическая ошибка тренда;
¾ средняя квадратическая ошибка тренда; ¾расчетное значение yt;
¾расчетное значение yt; ¾ значение t -статистики Стьюдента.
¾ значение t -статистики Стьюдента.
 , а
, а  .
.
 , а
, а  .
.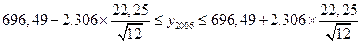
 .
.
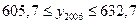 .
.

 .
.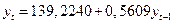

 .
.

 .
.

 .
.


