
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерии точности прогнозных расчетовСодержание книги
Поиск на нашем сайте
Рассчитанные по уравнению тренда оценки принято называть точечными, так как для каждого момента времени определяется только одно значение прогнозируемого показателя. Вероятность того, что реальное значение в будущем совпадет с прогнозной оценкой, невелика. Поэтому в дополнение к точечному прогнозу определяют границы возможного изменения прогнозируемого показателя, т.е., фактически вычисляют интервальный прогноз. Несовпадение фактических значений с точечным прогнозом может быть вызвано: 1) субъективной ошибкой при выборе вида кривой; 2) погрешностью оценивания параметров кривых; 3) погрешностью, связанной с отклонением отдельных наблюдений от кривой тренда. Погрешность, порождаемая вторым и третьим источником, может быть отражена в виде доверительного интервала прогнозного значения
где
Для линейной модели тренда дисперсия
где
Используя формулу (2.32), доверительный интервал можно представить в виде
Доверительные интервалы прогнозов, полученные с использованием нелинейных моделей (экспоненциальной, степенной и т.д.), определяются аналогичным образом. Отличие состоит только в том, что как при вычислении параметров кривой, так и при вычислении средней квадратической ошибки используются преобразованные значения уровней временного ряда (например, логарифмы). Важнейшими характеристиками качества прогнозной модели являются показатели ее точности. Показатели рассчитываются на основе ошибок прогноза. Ошибка прогноза – величина, характеризующая расхождение между фактическим и расчетным показателем. Она определяется по формуле
где
Наряду с ошибками (2.34) широко используются относительные ошибки прогноза, выраженные в процентах относительно фактических значений показателей
О точности модели нельзя сформировать правильное представление по отдельным прогнозным ошибкам, поэтому, кроме мгновенных характеристик (ошибка, относительная ошибка), используются средние характеристики по модулю (абсолютные, относительные)
При проведении сравнительной оценки моделей может также использоваться среднеквадратическая ошибка прогноза
Если приведенные характеристики вычисляются для перспективного периода, то их вычисление возможно только в том случае, когда станут известны фактические значения этого периода. Иногда в качестве меры качества прогнозной модели может стать
где
В случае, когда все прогнозы подтверждаются ( Коэффициент РЕГРЕССИОННЫЙ АНАЛИЗ И ПРОГНОЗ Множественная регрессия Основные понятия регрессионного анализа Рассмотренные в предыдущем разделе экстраполяционные модели иногда называют наивными в силу того, что в них не учитывается взаимодействие экономических показателей друг с другом. В реальности значение любого экономического показателя зависит от такого большого количества факторов, которое невозможно учесть при построении прогнозных моделей. Но в этом и нет необходимости, поскольку лишь ограниченное количество таких факторов существенно воздействует на моделируемый показатель. Доля влияния остальных столь незначительна, что их воздействием можно пренебречь без особого искажения реальной зависимости. Модели с ограниченным числом доминирующих факторов создают реальные предпосылки для их применения в анализе, прогнозировании и управлении в различных экономических ситуациях. Экономистами было исследовано достаточно большое число устоявшихся связей между различными показателями, которые пытаются использовать в задачах обоснования социально-экономических прогнозов. Однако даже устоявшиеся зависимости в одних и тех же ситуациях могут проявляться по-разному. В этой неоднозначности и состоит принципиальное отличие зависимостей между экономическими показателями от строгих функциональных зависимостей, используемых в естественных науках. Подобная неоднозначность объясняется целым рядом причин, в частности, тем, что, во-первых, при анализе влияние одной переменной на другую не учитывается ряд других факторов; во-вторых, это влияние может быть не прямым, а проявляться через цепочку других факторов; в-третьих, многие такие воздействия носят случайный характер и т.д. Поэтому в экономике принято рассматривать не функциональные, а статистические (корреляционные и регрессионные) зависимости. Корреляционная зависимость устанавливается в тех случаях, когда переменные Регрессионная зависимость определяется в тех случаях, когда одна из переменных
называемого функцией регрессии Пытаясь отразить тот факт, что реальные зависимости не всегда совпадают с ее условным математическим ожиданием и могут быть различными при одном и том же значении объясняющей переменной, в рассмотрение вводится случайная составляющая
называемого регрессионной моделью (уравнением).
|
||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 381; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.161.245 (0.006 с.) |

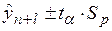 , (2.31)
, (2.31)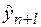 – точечный прогноз на момент
– точечный прогноз на момент 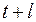 ;
;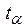 – значение t -статистики Стьюдента;
– значение t -статистики Стьюдента;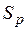 – средняя квадратическая ошибка прогноза;
– средняя квадратическая ошибка прогноза;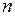 – длина временного ряда;
– длина временного ряда;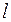 – период упреждения.
– период упреждения.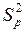 может быть представлена в виде
может быть представлена в виде
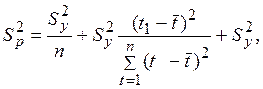 (2.32)
(2.32)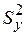 – дисперсия отклонений фактических наблюдений от расчетных;
– дисперсия отклонений фактических наблюдений от расчетных;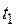 – время упреждения, для которого делается экстраполяция,
– время упреждения, для которого делается экстраполяция, 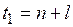 ;
;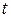 – порядковый номер уровней ряда,
– порядковый номер уровней ряда, 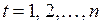 ;
;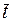 – порядковый номер уровня, стоящего в середине ряда.
– порядковый номер уровня, стоящего в середине ряда.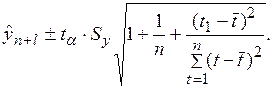 (2.33)
(2.33)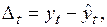 (2.34)
(2.34)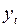 – фактическое значение показателя;
– фактическое значение показателя;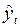 – прогнозное значение показателя.
– прогнозное значение показателя.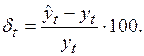 (2.35)
(2.35) (2.36)
(2.36)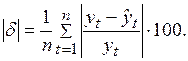 (2.37)
(2.37)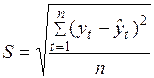 . (2.38)
. (2.38)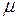 – относительное число случаев, когда фактическое значение охватывалось интервальным прогнозом
– относительное число случаев, когда фактическое значение охватывалось интервальным прогнозом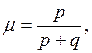 (2.39)
(2.39)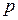 – число прогнозов, подтвержденных фактическими данными;
– число прогнозов, подтвержденных фактическими данными;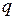 – число прогнозов, не подтвержденных фактическими данными.
– число прогнозов, не подтвержденных фактическими данными. ), то
), то 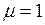 . Если ни один прогноз не подтверждается (
. Если ни один прогноз не подтверждается (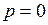 ), то
), то 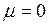 .
. и
и 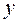 считаются равноценными в том смысле, что они не подразделяются на независимую (причину) и зависимую (следствие). При решении прогнозных задач самостоятельной роли корреляционный анализ не играет и чаще всего используется как инструмент отбора значимых факторов.
считаются равноценными в том смысле, что они не подразделяются на независимую (причину) и зависимую (следствие). При решении прогнозных задач самостоятельной роли корреляционный анализ не играет и чаще всего используется как инструмент отбора значимых факторов.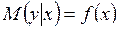 , (3.1)
, (3.1)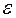 , с помощью которой зависимость между объясняющей и объясняемой переменной записывается в виде соотношения
, с помощью которой зависимость между объясняющей и объясняемой переменной записывается в виде соотношения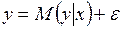 , (3.2)
, (3.2)


