
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Экстраполяция временных рядовСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
ЭКСТРАПОЛЯЦИЯ ВРЕМЕННЫХ РЯДОВ Сущность экстраполяции Методы экстраполяции тенденций в развитии экономических процессов являются, пожалуй, наиболее часто применяемыми среди всей совокупности методов прогнозирования. В общем случае под экстраполяцией принято понимать распространение (возможно, с преобразованиями, осуществляемыми посредством формальных методов) количественных характеристик каких-либо объектов или процессов, наблюдаемых в определенных временных, пространственных либо других границах за эти границы. Формально это означает, что значения некоторой функции определяются за границей области ее определения. В экономических прогнозных расчетах использование экстраполяции имеет в своей основе предположение о том, что рассматриваемый процесс изменения прогнозируемой переменной представляет собой сочетание двух составляющих: регулярной и случайной:
Считается, что регулярная составляющая Случайная составляющая Успех применения эктраполяционных методов прогнозирования в значительной степени зависит от выбора наилучшего в некотором смысле описания (вида) тренда.
Метод наименьших квадратов (МНК) Простейшую экстраполяционную модель, отражающую взаимосвязь прогнозируемого показателя с некоторой переменной, формирующей динамику этого показателя, можно записать в виде
где
Чем ниже уровень вариаций около 0 возможных значений случайной величины
В общем случае поиск оптимальных параметров
который значительно упрощает решение этой задачи. Рассмотрим применение метода наименьших квадратов к случаю построения линейного тренда. Для этого случая (2.22) перепишется в виде
Применяя дифференциальное исчисление для минимизации (2.24) и дифференцируя по
Разделив левую и правую части этой системы на число наблюдений
перепишем систему (2.25) в виде
РЕГРЕССИОННЫЙ АНАЛИЗ И ПРОГНОЗ Множественная регрессия Основные понятия регрессионного анализа Рассмотренные в предыдущем разделе экстраполяционные модели иногда называют наивными в силу того, что в них не учитывается взаимодействие экономических показателей друг с другом. В реальности значение любого экономического показателя зависит от такого большого количества факторов, которое невозможно учесть при построении прогнозных моделей. Но в этом и нет необходимости, поскольку лишь ограниченное количество таких факторов существенно воздействует на моделируемый показатель. Доля влияния остальных столь незначительна, что их воздействием можно пренебречь без особого искажения реальной зависимости. Модели с ограниченным числом доминирующих факторов создают реальные предпосылки для их применения в анализе, прогнозировании и управлении в различных экономических ситуациях.
Экономистами было исследовано достаточно большое число устоявшихся связей между различными показателями, которые пытаются использовать в задачах обоснования социально-экономических прогнозов. Однако даже устоявшиеся зависимости в одних и тех же ситуациях могут проявляться по-разному. В этой неоднозначности и состоит принципиальное отличие зависимостей между экономическими показателями от строгих функциональных зависимостей, используемых в естественных науках. Подобная неоднозначность объясняется целым рядом причин, в частности, тем, что, во-первых, при анализе влияние одной переменной на другую не учитывается ряд других факторов; во-вторых, это влияние может быть не прямым, а проявляться через цепочку других факторов; в-третьих, многие такие воздействия носят случайный характер и т.д. Поэтому в экономике принято рассматривать не функциональные, а статистические (корреляционные и регрессионные) зависимости. Корреляционная зависимость устанавливается в тех случаях, когда переменные Регрессионная зависимость определяется в тех случаях, когда одна из переменных
называемого функцией регрессии Пытаясь отразить тот факт, что реальные зависимости не всегда совпадают с ее условным математическим ожиданием и могут быть различными при одном и том же значении объясняющей переменной, в рассмотрение вводится случайная составляющая
называемого регрессионной моделью (уравнением). ЭКСТРАПОЛЯЦИЯ ВРЕМЕННЫХ РЯДОВ Сущность экстраполяции Методы экстраполяции тенденций в развитии экономических процессов являются, пожалуй, наиболее часто применяемыми среди всей совокупности методов прогнозирования. В общем случае под экстраполяцией принято понимать распространение (возможно, с преобразованиями, осуществляемыми посредством формальных методов) количественных характеристик каких-либо объектов или процессов, наблюдаемых в определенных временных, пространственных либо других границах за эти границы. Формально это означает, что значения некоторой функции определяются за границей области ее определения.
В экономических прогнозных расчетах использование экстраполяции имеет в своей основе предположение о том, что рассматриваемый процесс изменения прогнозируемой переменной представляет собой сочетание двух составляющих: регулярной и случайной:
Считается, что регулярная составляющая Случайная составляющая Успех применения эктраполяционных методов прогнозирования в значительной степени зависит от выбора наилучшего в некотором смысле описания (вида) тренда.
|
|||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 1202; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.116.231 (0.01 с.) |

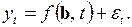 (2.1)
(2.1)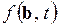 представляет собой гладкую функцию от аргумента, в качестве которого обычно рассматривается время. Функция определяется с точностью до неизвестного вектора параметров
представляет собой гладкую функцию от аргумента, в качестве которого обычно рассматривается время. Функция определяется с точностью до неизвестного вектора параметров 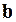 , который остается неизменным на периоде упреждения прогноза. Эту составляющую называют трендом, или уровнем детерминированной основы процесса, или основной тенденцией. Под всеми этими терминами понимается интуитивное представление о какой-то «очищенной» от случайных колебаний закономерности анализируемого процесса. Интуитивное – потому, что для большинства экономических процессов нельзя однозначно отделить тренд от случайной составляющей. Все зависит от того, какую цель преследует подобное разделение, и с какой точностью его хотят осуществить.
, который остается неизменным на периоде упреждения прогноза. Эту составляющую называют трендом, или уровнем детерминированной основы процесса, или основной тенденцией. Под всеми этими терминами понимается интуитивное представление о какой-то «очищенной» от случайных колебаний закономерности анализируемого процесса. Интуитивное – потому, что для большинства экономических процессов нельзя однозначно отделить тренд от случайной составляющей. Все зависит от того, какую цель преследует подобное разделение, и с какой точностью его хотят осуществить. обычно считается ненаблюдаемым некоррелированным случайным процессом с нулевым математическим ожиданием и ограниченной дисперсией. Его оценки получаются только после построения модели и в дальнейшем используются для определения интервальных характеристик точности прогноза.
обычно считается ненаблюдаемым некоррелированным случайным процессом с нулевым математическим ожиданием и ограниченной дисперсией. Его оценки получаются только после построения модели и в дальнейшем используются для определения интервальных характеристик точности прогноза.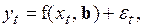
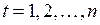 , (2.21)
, (2.21)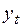 – значение
– значение 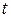 -го наблюдения прогнозируемого показателя;
-го наблюдения прогнозируемого показателя;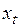 – значение переменой, формирующей динамику показателя в момент времени
– значение переменой, формирующей динамику показателя в момент времени 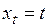 );
);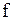 – функция, определяющая структуру трендовой модели (линейную, степенную и т.п.);
– функция, определяющая структуру трендовой модели (линейную, степенную и т.п.);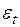 – ненаблюдаемая случайная величина, представляющая собой ту часть вариации показателя
– ненаблюдаемая случайная величина, представляющая собой ту часть вариации показателя 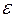 , тем точнее модель отражает взаимодействие переменной
, тем точнее модель отражает взаимодействие переменной 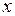 с прогнозируемым показателем
с прогнозируемым показателем 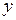 , т.е. параметры модели должны подбираться таким образом, чтобы минимизировать сумму квадратов отклонений (случайных составляющих
, т.е. параметры модели должны подбираться таким образом, чтобы минимизировать сумму квадратов отклонений (случайных составляющих  . (2.22)
. (2.22)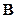 сводится к решению нелинейной экстремальной задачи. Обычно рассматривают линейный случай
сводится к решению нелинейной экстремальной задачи. Обычно рассматривают линейный случай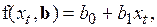 (2.23)
(2.23) (2.24)
(2.24)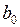 и
и 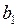 , получаем систему линейных уравнений
, получаем систему линейных уравнений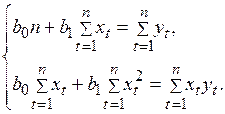 (2.25)
(2.25)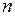 и произведя замену:
и произведя замену: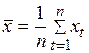 ;
; 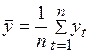 ;
; 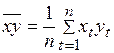 ;
; 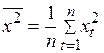 ,
,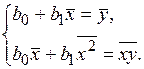 (2.26)
(2.26) и
и 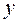 считаются равноценными в том смысле, что они не подразделяются на независимую (причину) и зависимую (следствие). При решении прогнозных задач самостоятельной роли корреляционный анализ не играет и чаще всего используется как инструмент отбора значимых факторов.
считаются равноценными в том смысле, что они не подразделяются на независимую (причину) и зависимую (следствие). При решении прогнозных задач самостоятельной роли корреляционный анализ не играет и чаще всего используется как инструмент отбора значимых факторов.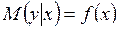 , (3.1)
, (3.1)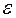 , с помощью которой зависимость между объясняющей и объясняемой переменной записывается в виде соотношения
, с помощью которой зависимость между объясняющей и объясняемой переменной записывается в виде соотношения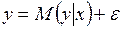 , (3.2)
, (3.2)


