
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аналитическое сглаживание временногоСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Ряда. Уравнение тренда. Кривые роста, описывающие закономерности развития явлений во времени, - это результат аналитического выравнивания динамических рядов. Выравнивание ряда с помощью тех или иных функций (т. е. их подгонка к данным) в большинстве случаев оказывается удобным средством описания эмпирических данных. Это средство при соблюдении ряда условий можно применить и для прогнозирования. Процесс выравнивания состоит из следующих основных этапов: - выбора типа кривой, форма которой соответствует характеру изменения динамического ряда; - определения численных значений (оценивание) параметров кривой; - апостериорного контроля качества выбранного тренда. В современных ППП все перечисленные этапы реализуются одновременно, как правило, в рамках одной процедуры. Аналитическое сглаживание с использованием той или иной функции позволяет получить выравненные, или, как их иногда не вполне правомерно называют, теоретические значения уровней динамического ряда, т. е. те уровни, которые наблюдались бы, если бы динамика явления полностью совпадала с кривой. Эта же функция с некоторой корректировкой или без нее, применяется в качестве модели для экстраполяции (прогноза). Вопрос о выборе типа кривой является основным при выравнивании ряда. При всех прочих равных условиях ошибка в решении этого вопроса оказывается более значимой по своим последствиям (особенно для прогнозирования), чем ошибка, связанная со статистическим оцениванием параметров. Поскольку форма тренда объективно существует, то при выявлении ее следует исходить из материальной природы изучаемого явления, исследуя внутренние причины его развития, а также внешние условия и факторы на него влияющие. Только после глубокого содержательного анализа можно переходить к использованию специальных приемов, разработанных статистикой. Весьма распространенным приемом выявления формы тренда является графическое изображение временного ряда. Но при этом велико влияние субъективного фактора, даже при отображении выровненных уровней. Наиболее надежные методы выбора уравнения тренда основаны на свойствах различных кривых, применяемых при аналитическом выравнивании. Такой подход позволяет увязать тип тренда с теми или иными качественными свойствами развития явления. Нам представляется, что в большинстве случаев практически приемлемым является метод, который основывается на сравнении характеристик изменения приростов исследуемого динамического ряда с соответствующими характеристиками кривых роста. Для выравнивания выбирается та кривая, закон изменения прироста которой наиболее близок к закономерности изменения фактических данных. В табл. 4 приводится перечень наиболее употребительных при анализе экономических рядов видов кривых и указываются соответствующие «симптомы», по которым можно определить, какой вид кривых подходит для выравнивания. При выборе формы кривой надо иметь в виду еще одно обстоятельство. Рост сложности кривой в целом ряде случаев может действительно увеличить точность описания тренда в прошлом, однако в связи с тем, что более сложные кривые содержат большее число параметров и более высокие степени независимой переменной, их доверительные интервалы будут в общем существенно шире, чем у более простых кривых при одном и том же периоде упреждения. Таблица 4 Характер изменения показателей, основанных
В настоящее время, когда использование специальных программ без особых усилий позволяет одновременно строить несколько видов уравнений, широко эксплуатируются формальные статистические критерии для определения лучшего уравнения тренда. Из сказанного выше, по-видимому, можно сделать вывод о том, что выбор формы кривой для выравнивания представляет собой задачу, которая не решается однозначно, а сводится к получению ряда альтернатив. Окончательный выбор не может лежать в области формального анализа, тем более, если предполагается с помощью выравнивания не только статистически описать закономерность поведения уровня в прошлом, но и экстраполировать найденную закономерность в будущее. Вместе с тем различные статистические приемы обработки данных наблюдения могут принести существенную пользу, по крайней мере, с их помощью можно отвергнуть заведомо непригодные варианты и тем самым существенно ограничить поле выбора. Рассмотрим наиболее используемые типы уравнений тренда: 1.Линейная форма тренда:
где
Для линейной формы тренда характерно равенство так называемых первых разностей (абсолютных приростов) и нулевые вторые разности, т. е. ускорения. 2.Параболическая (полином 2-ой степени) форма тренда:
Для данного типа кривой постоянными являются вторые разности (ускорение), а нулевыми – третьи разности. Параболическая форма тренда соответствует ускоренному или замедленному изменению уровней ряда с постоянным ускорением. Если 3.Экспоненциальная форма тренда:
где При 4.Гиперболическая форма тренда (1 типа):
Данная форма тренда может отображать тенденцию процессов, ограниченных предельным значением уровня. 5.Логарифмическая форма тренда:
где Логарифмическим трендом может быть описана тенденция, проявляющаяся в замедлении роста уровней ряда динамики при отсутствии предельно возможного значения. При достаточно большом t логарифмическая кривая становится мало отличимой от прямой линии. 6.Обратнологарифмическая форма тренда:
7.Мультипликативная (степенная) форма тренда:
8.Обратная (гиперболическая 2 типа) форма тренда:
9.Гиперболическая форма тренда 3 типа:
10.Полином 3-ей степени:
Для всех нелинейных, относительно исходных переменных моделей (уравнений регрессии), а их здесь большинство, требуется провести вспомогательные преобразования, представленные в таблице ниже. Таблица 5 Модели, сводящиеся к линейному тренду
В формулах, перечисленных в таблице, как и во всех формулах, описывающих модель тренда, Однако, при практическом использовании линеаризации с помощью преобразования исследуемых переменных следует иметь ввиду, что оценки параметров, полученных линеаризацией с помощью М.Н.К. (метод наименьших квадратов), минимизируют сумму квадратов отклонений для преобразованных, а не исходных переменных. Поэтому полученные с помощью линеаризации зависимостей оценки нуждаются в уточнении. Для решения поставленной задачи по аналитическому сглаживанию динамических рядов в системе STATISTICA нам потребуется создать несколько новых дополнительных переменных, необходимых для выполнения дальнейшей работы, а также осуществить некоторые вспомогательные операции по преобразованию нелинейных моделей тренда в линейные. Итак, нам предстоит построить уравнение тренда, которое по существу является уравнением регрессии, в котором в качестве фактора выступает «время». Прежде всего, мы создадим переменную «Т», содержащую моменты времени четвертого периода. Так как четвертый период включает 12 лет, то переменная «Т» будет состоять из натуральных чисел от 1 до 12, соответствующих месяцам года. Кроме того, для работы с некоторыми моделями тренда нам потребуется еще несколько переменных, содержание которых можно понять из их обозначения. Это переменные, получаемые из временного ряда: «Т^2», «Т^3», «1/Т» и «ln T». А также переменные, получаемые из исходных данных за четвертый период: «1/Import4» и «ln Import4». Также необходимо создать такую же таблицу для экспорта. Все это предлагается сделать на новом рабочем листе, скопировав туда данные за 4-й период. Для этого воспользуемся уже известным нам меню Workbook/Insert. В итоге получаем следующие электронные таблицы.
Рис. 38. Таблица со вспомогательными переменными для импорта
Рис. 39. Таблица со вспомогательными переменными для экспорта
Для аналитического выравнивания рядов динамики мы будем использовать модуль Multiple Regression в меню Statistics. Рассмотрим пример построения графического изображения и определение численных параметров тренда, выраженного линейной зависимостью.
Рис. 40. Модуль Multiple Regression в меню Statistics
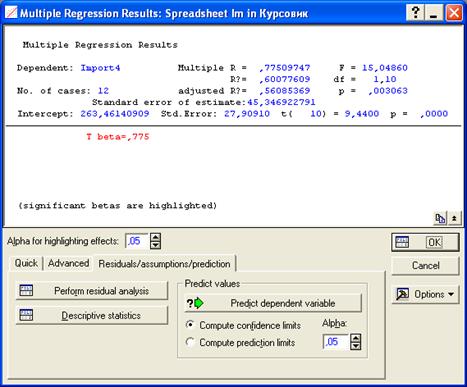
Для выбора зависимых и независимых переменных воспользуемся кнопкой Variables. В открывшемся окне в левом информационном поле мы выбираем зависимую переменную Yt, (в нашем случае это Import 4 – данные по четвертому периоду). Номера выбранных зависимых переменных отображаются внизу в поле Dependent var. (or list for batch). Соответственно в правом поле мы выбираем независимые переменные (в нашем случае одну – время «Т»). Номера выбранных независимых переменных высвечиваются внизу в поле Independent variable list. После того, как завершен выбор переменных, нажимаем ОК. Система выдает окно с обобщенными результатами расчета параметров тренда (далее они будут рассмотрены более подробно) и возможностью выбора направления для последующего детального анализа. Заметим, что значение оценки, высвеченное красным цветом, указывает на статистическую значимость результатов. Далее переходим к закладке Advanced.
Рис. 41. Закладка Advanced
На закладке располагается несколько кнопок, позволяющих получить максимально детализированные сведения по интересующему нас направлению анализа. При нажатии на нее получаем две таблицы с результатами регрессионного анализа. В первой представлены результаты расчета параметров уравнения регрессии, во второй – основные показатели уравнения.
Рис. 42. Основные показатели уравнения для данных импорта за четвертый период (линейный тренд) Здесь N = – объем результативной переменной. В верхнем поле расположены показатели R,
Рис. 43. Параметры уравнения регрессии для данных импорта за четвертый период (линейный тренд)
Для оценки статистической значимости уравнения в целом на закладке Advanced воспользуемся кнопкой ANOVA (Goodness Of Fit), позволяющей получить таблицу дисперсионного анализа и значение F-критерия Фишера.
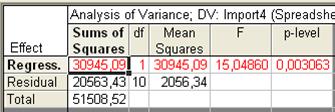
Рис. 44. Таблица дисперсионного анализа
Sums of Squares – сумма квадратов отклонений: на пересечении со строкой Regression – сумма квадратов отклонений теоретических (полученных по уравнению регрессии) значений признака от средней величины. Эта сумма квадратов используется для расчета факторной, объясненной дисперсии зависимой переменной. На пересечении со строкой Residual – сумма квадратов отклонений теоретических и фактических значений переменной (для расчета остаточной, необъясненной дисперсии), Total – отклонений фактических значений переменной от средней величины (для расчета общей дисперсии). Столбец df – число степеней свободы, Means Squares обозначает дисперсию: на пересечении со строкой Regression – факторную, со строкой Residual - остаточную, F – критерий Фишера, используемый для оценки общей значимости уравнения и коэффициента детерминации, p-level – уровень значимости. Параметры уравнения тренда в STATISTICA, как и в большинстве других программ, рассчитываются по метод наименьших квадратов (МНК). Метод позволяет получить значения параметров, при которых обеспечивается минимизация суммы квадратов отклонений фактических уровней от сглаженных, т. е. полученных в результате аналитического выравнивания.
Математический аппарат метода наименьших квадратов описан в большинстве работ по математической статистике, поэтому нет необходимости подробно на нем останавливаться. Напомним только некоторые моменты. Так, для нахождения параметров линейного тренда (2.10) необходимо решить систему уравнений:
Данная система уравнений упрощается, если значения t подобрать таким образом, чтобы их сумма равнялась нулю, т. е. начало отсчета времени перенести в середину рассматриваемого периода. Очевидно, что перенос начала координат имеет смысл только при ручной обработке динамического ряда. Если
В общем виде систему уравнений для нахождения параметров полинома
При сглаживании временного ряда по экспоненте (которая часто используется в экономических исследованиях) Далее решается система нормальных уравнений:
После переноса начала отсчета времени в середину ряда получают:
следовательно:
Если наблюдаются более сложные изменения уровней временного ряда и выравнивание осуществляется по показательной функции вида
В практике исследования социально-экономических явлений исключительно редко встречаются динамические ряды, характеристики которых полностью соответствуют признакам эталонных математических функций. Это обусловлено значительным числом факторов разного характера, влияющих на уровни ряда и тенденцию их изменения. На практике чаще всего строят целый ряд функций, описывающих тренд, а затем выбирают лучшую на основе того или иного формального критерия. Далее возвращаемся к текущему анализу и переходим на закладку Residuals/Assumptions/Prediction того же диалогового окна.
Рис. 45. Закладка Residuals/Assumptions/Prediction
Здесь воспользуемся кнопкой Perform Residual Analysis, открывающую модуль анализа остатков. Под остатками (Residuals) в данном случае понимается отклонение исходных значений динамического ряда от прогнозируемых, в соответствии с выбранным уравнением тренда. Сразу же переходим к закладке Advanced.
Рис. 46. Закладка Advanced в Perform Residual Analysis
Воспользуемся кнопкой Summary: Residuals & Predicted, позволяющую получить одноименную таблицу, которая содержит исходные значения динамического ряда Observed Value, прогнозируемые значения по выбранной модели тренда Predicted Value, отклонения прогнозных значений от исходных Residual Value, а также различные специальные показатели и стандартизированные значения. Также в таблице представлены максимальное, минимальное значения, средняя и медиана по каждому столбцу.
Рис. 47. Таблица, содержащая показатели и специальные значения для линейного тренда
В данной таблицы наибольший интерес для нас представляет столбец Residual Value, значения которого в дальнейшем используются для характеристики качества подбора тренда, а также столбец Predicted Value, который содержит прогнозные значения динамического ряда в соответствии с выбранной моделью тренда (в нашем случае – линейной). Далее построим график исходного временного ряда совместно с вычисленными в соответствии с линейным уравнением тренда прогнозными значениями для четвертого периода. Для этого лучше всего скопировать значения из столбца Predicted Value в таблицу, в которой были созданы переменные для построения трендов.
Рис. 48. Третий период динамического ряда импорта (млрд. $) и линейный тренд
Итак, мы получили все необходимые результаты расчета параметров тренда, выраженного линейной моделью, для четвертого периода исходного динамического ряда, а также построили график данного ряда, совмещенный с линией тренда. Далее будут представлены остальные модели трендов. Следует заметить, что в результате линеаризации степенной и экспоненциальной функций STATISTICA возвращает значение линеаризованной функции равное Для этого также целесообразно создать дополнительные переменные и получить их с помощью формул на основе уже имеющихся переменных. Далее рассмотрим пример построения таблиц и графиков с использованием линеаризации на примере степенной функции. Итак, при решении задачи с помощью процедуры Multiple Regression, необходимо в качестве переменных выбрать натуральные логарифмы исходного ряда и оси времени. Далее проходит тот же путь, что и при построении линейной модели и получаем три таблицы.
Рис. 49. Основные показатели уравнения для данных импорта за третий период (степенная модель)
Рис. 50. Параметры уравнения регрессии для данных импорта за третий период (степенная модель)
Рис. 51. Таблица дисперсионного анализа
Рис. 52. Таблица, содержащая показатели и специальные значения для степенной модели
Затем, как и в случае с линейным трендом, копируем значения из столбца Predicted Value в таблицу, но там для этого строим еще одну переменную, в которой получаем прогнозные значения по степенной функции с помощью преобразования
Рис. 53. Создание дополнительной переменной
Рис. 54. Таблица со всеми переменными
Рис. 55. Третий период динамического ряда импорта (млрд. $) и степенная модель
Рис.56. Основные показатели уравнения для данных импорта за третий период (экспоненциальная модель)
Рис. 57. Третий период динамического ряда импорта (млрд. $) и экспоненциальная модель
Рис.58. Основные показатели уравнения для данных импорта за третий период (обратная модель)
Рис. 59. Третий период динамического ряда импорта (млрд. $) и обратная модель
Рис. 60. Основные показатели уравнения для данных импорта за третий период (полином второй степени)
Рис. 61. Третий период динамического ряда импорта (млрд. $) и полином второй степени
Рис. 62. Основные показатели уравнения для данных импорта за третий период (полином 3-й степени)
Рис. 63. Третий период динамического ряда импорт (млрд. $) и полином 3-й степени
Рис. 64. Основные показатели уравнения для данных импорта за третий период (гипербола 1-ого вида)
Рис. 65. Третий период динамического ряда импорт (млрд. $) и гипербола 1-ого вида
Рис. 66. Основные показатели уравнения для данных импорта за третий период (гипербола 3 типа)
Рис. 67. Третий период динамического ряда импорт и гипербола 3 типа
Рис. 68. Основные показатели уравнения для данных импорта за третий период (логарифмическая модель)
Рис. 69. Третий период динамического ряда импорт (млрд. $) и логарифмическая модель
Рис. 70. Основные показатели уравнения для данных импорта за третий период (обратнологарифмическая модель)
Рис. 71. Третий период динамического ряда импорт (млрд. $) и обратнологарифмическая модель
Затем построим таблицу со вспомогательными переменными для построения трендов для экспорта.
Рис. 72. Таблица со вспомогательными переменными
Проделаем те же операции что и для четвертого период импорта.
Рис. 73. Основные показатели уравнения для данных экспорта за третий период (линейная модель)
Рис. 74. Третий период динамического ряда экспорта (млрд. $) и линейная модель
Рис. 75. Основные показатели уравнения для данных экспорта за третий период (степенная модель тренда)
Рис. 76. Третий период динамического ряда экспорта и степенная модель
Рис. 77. Основные показатели уравнения для данных экспорта за третий период (экспоненциальная модель тренда)
Рис. 78. Третий период динамического ряда экспорта (млрд. $) и экспоненциальная модель
Рис. 79. Основные показатели уравнения для данных экспорта за третий период (обратная модель тренда)
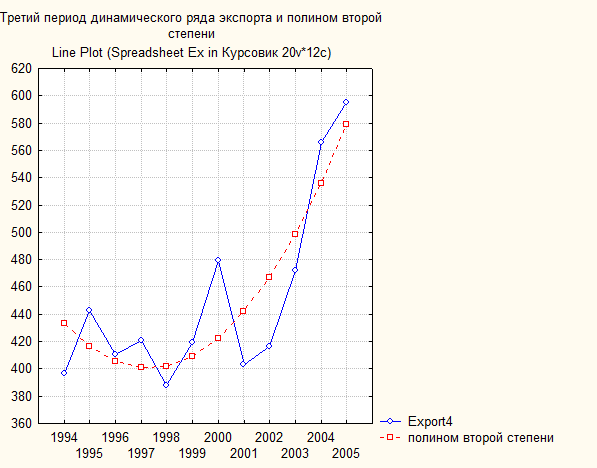
Рис. 81. Основные показатели уравнения для данных экспорта за третий период (полином второй степени)
Рис. 82. Третий период динамического ряда экспорта (млрд. $) и полином второй степени
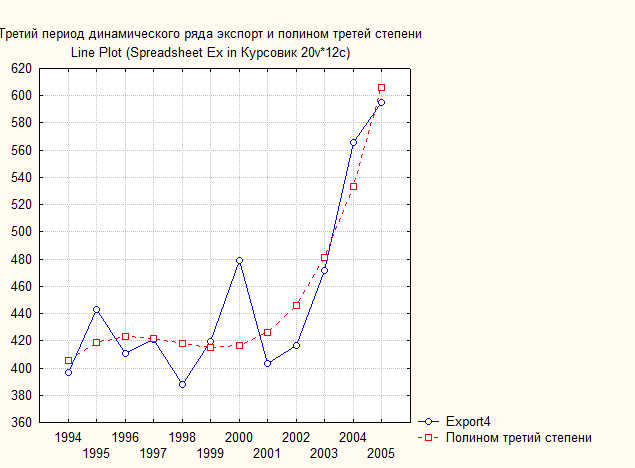
Рис. 83. Основные показатели уравнения для данных экспорта за третий период (полином третей степени)
Рис. 84. Третий период динамического ряда экспорта (млрд. $) и полином третей степени
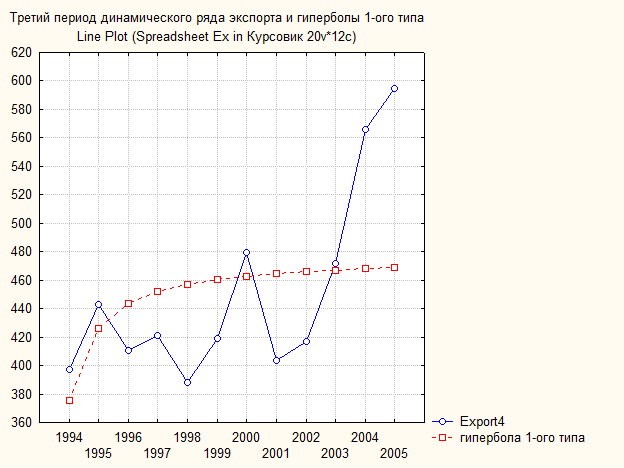
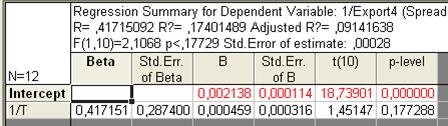
Рис. 85. Основные показатели уравнения для данных экспорта за третий период (гипербола 1-ого вида)
Рис. 86. Третий период динамического ряда экспорта и гипербола 1-ого типа
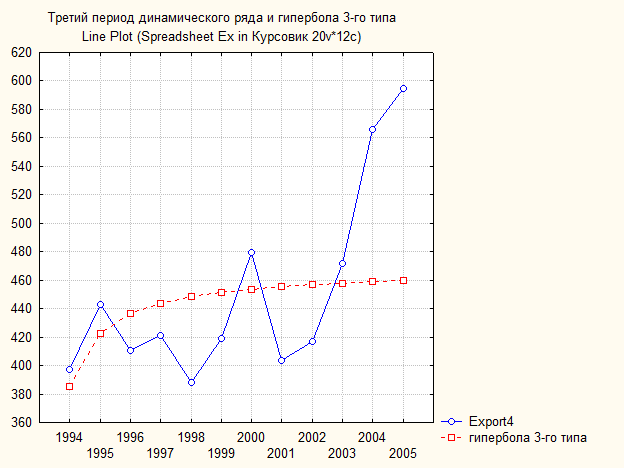
Рис. 87. Основные показатели уравнения для данных экспорта за третий период (гипербола 3-ого вида)
Рис. 88. Третий период динамического ряда экспорта (млрд. $) и гипербола 3-ого типа
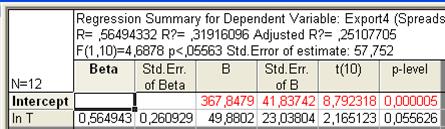
Рис. 89. Основные показатели уравнения для данных экспорта за третий период (логарифмическая модель)
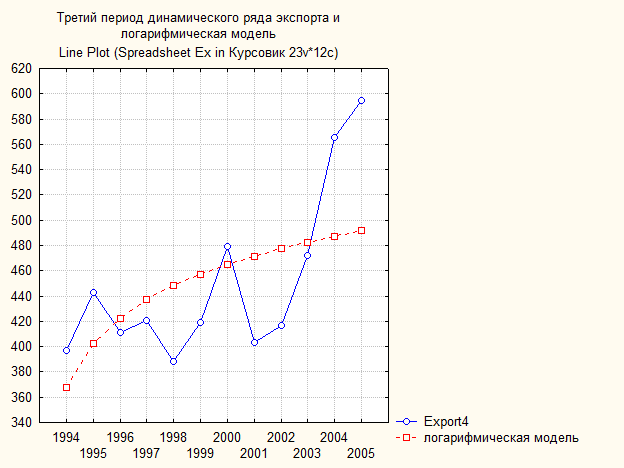
Рис. 90. Третий период динамического ряда экспорта (млрд. $) и логарифмическая модель
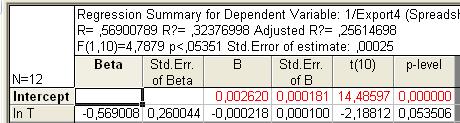
Рис. 91. Основные показатели уравнения для данных экспорта за третий период (обратнологарифмическая модель)
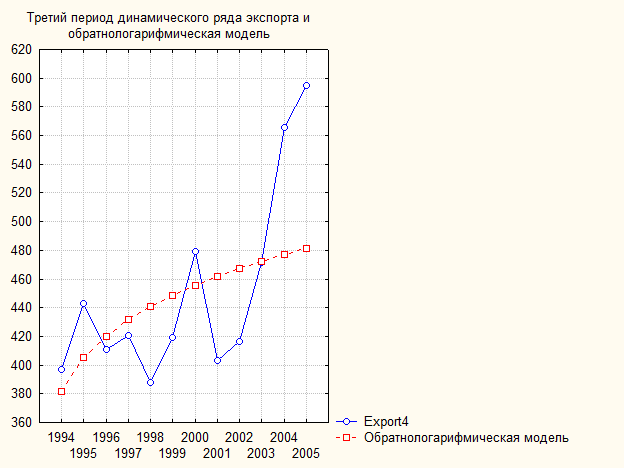
Рис. 91. Третий период динамического ряда экспорта (млрд. $) и обратнологарифмическая модель
Выбор наилучшего тренда
Как уже отмечалось, проблема выбора формы кривой — одна из основных проблем, с которой сталкиваются при выравнивании ряда динамики. Решение этой проблемы во многом определяет результаты экстраполяции тренда. В большинстве специализированных программ для выбора лучшего уравнения тренда предоставляется возможность воспользоваться следующими критериями: - минимальное значение среднеквадратической ошибки тренда:
где
n - число уровней ряда; p - число факторовв уравнении тренда. - минимальное значение остаточной дисперсии:
- минимальное значение средней ошибки аппроксимации; - минимальное значение средней абсолютной ошибки; - максимальное значение коэффициента детерминации; - максимальное значение F- критерия Фишера:
где k – число степеней свободы факторной дисперсии,равное числу независимых переменных (признаков-факторов) в уравнении; n-k-1 - число степеней свободы остаточной дисперсии. Применение формального критерия для выбора формы кривой, по-видимому, даст практически пригодные результаты в том случае, если отбор будет проходить в два этапа. На первом этапе отбираются зависимости, пригодные с позиции содержательного подхода к задаче, в результате чего происходит ограничение круга потенциально приемлемых функций. На втором этапе для этих функций подсчитываются значения критерия и выбирается та из кривых, которой соответствует минимальное его значение. В данном пособии для идентификации тренда используется формальный метод, который основывается на использовании численного критерия. В качестве такого критерия рассматривается максимальный коэффициент детерминации:
Расшифровка обозначений и формулы данных показателей даны в предыдущих разделах. Коэффициент детерминации показывает, какая доля общей дисперсии результативного признака обусловлена вариацией признака – фактора. В таблицах STATISTICA он обозначается как R?. В следующей ниже таблице будут представлены уравнения моделей трендов и коэффициенты детерминации данных импорта.
Таблица 6 Уравнения моделей трендов и коэффициенты детерминации Import.
Составим такую же таблицу для данных по экспорту.
Таблица 7 Уравнения моделей трендов и коэффициенты детерминации Export.
Сопоставив значения коэффициентов детерминации для различных типов кривых можно сделать вывод о том, что для исследуемого третьего периода лучшей формой тренда будет полином третей степени для импорта и для экспорта. Далее необходимо проанализировать выбранную модель тренда с точки зрения ее адекватности реальным тенденциям исследуемого временного ряда через оценку надежности полученных уравнений трендов по F-критерию Фишера. В данном случае расчетное значение критерия Фишера для импорта равно 16,573; для экспорта – 13,098, а табличное значение при уровне значимости Важнейшим элементом оценки качества выбранной модели является анализ автокорреляции в остатках, т.е. в отклонениях исходных значений динамического ряда от рассчитанных по уравнению тренда. Если аппроксимация удовлетворительная, то случайные составляющие – отклонения от тренда
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 2303; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.31.17 (0.016 с.) |


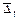
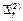
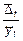
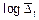
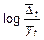
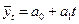 ,
,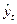 - уровень ряда, полученный в результате выравнивания по прямой;
- уровень ряда, полученный в результате выравнивания по прямой; - начальный уровень тренда;
- начальный уровень тренда; - средний абсолютный прирост; константа тренда.
- средний абсолютный прирост; константа тренда.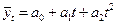
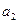 < 0 и
< 0 и 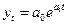 ,
,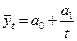
 ,
,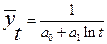
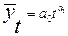
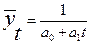

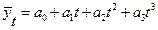
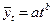
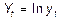
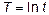
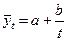
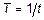
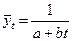
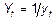
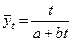
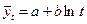
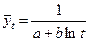
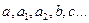 есть коэффициенты уравнений.
есть коэффициенты уравнений.

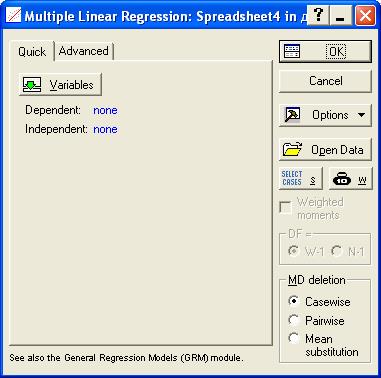
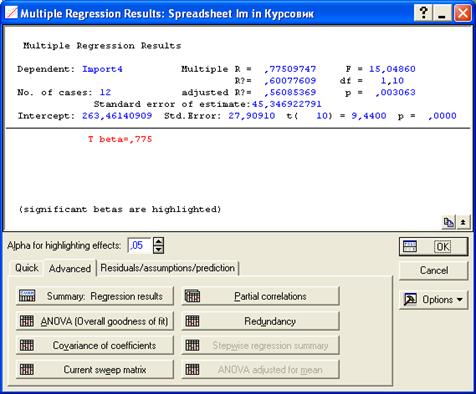
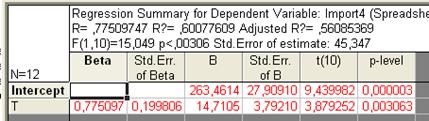
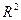 , Adjusted R, F, p, Std.Error of Estimate, означающие соответственно теоретическое корреляционное отношение, коэффициент детерминации, уточненный коэффициент детерминации, расчетное значение критерия Фишера (в скобках дано число степеней свободы), уровень значимости, стандартная ошибка уравнения (эти же показатели можно увидеть во второй таблице). В самой таблице нас интересуют столбец В, в котором расположены коэффициенты уравнения, столбец t и столбец p-level, обозначающие расчетное значение t-критерия и расчетный уровень значимости, необходимые для оценки значимости параметров уравнения. При этом система помогает пользователю: когда процедура предполагает проверку на значимость, STATISTICA выделяет значимые элементы красным цветом (т.е. отвергается нулевая гипотеза о равенстве параметров нулю). В нашем случае |tфакт| > tтабл для обоих параметров, следовательно они значимы.
, Adjusted R, F, p, Std.Error of Estimate, означающие соответственно теоретическое корреляционное отношение, коэффициент детерминации, уточненный коэффициент детерминации, расчетное значение критерия Фишера (в скобках дано число степеней свободы), уровень значимости, стандартная ошибка уравнения (эти же показатели можно увидеть во второй таблице). В самой таблице нас интересуют столбец В, в котором расположены коэффициенты уравнения, столбец t и столбец p-level, обозначающие расчетное значение t-критерия и расчетный уровень значимости, необходимые для оценки значимости параметров уравнения. При этом система помогает пользователю: когда процедура предполагает проверку на значимость, STATISTICA выделяет значимые элементы красным цветом (т.е. отвергается нулевая гипотеза о равенстве параметров нулю). В нашем случае |tфакт| > tтабл для обоих параметров, следовательно они значимы.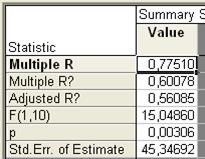


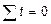 , то
, то 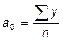 ,
,  .
.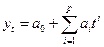 можно записать как
можно записать как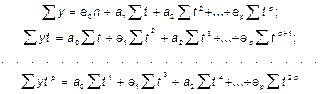

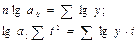

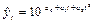 , то параметры определяются в результате решения следующей системы уравнений:
, то параметры определяются в результате решения следующей системы уравнений: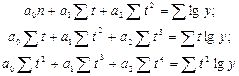


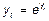 , в том числе и для построения графических изображений. Для гиперболических функций, а также для обратнологарифмической функции необходимо выполнить преобразование вида
, в том числе и для построения графических изображений. Для гиперболических функций, а также для обратнологарифмической функции необходимо выполнить преобразование вида 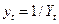 .
.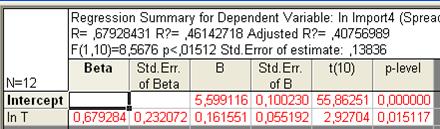

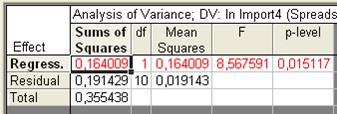
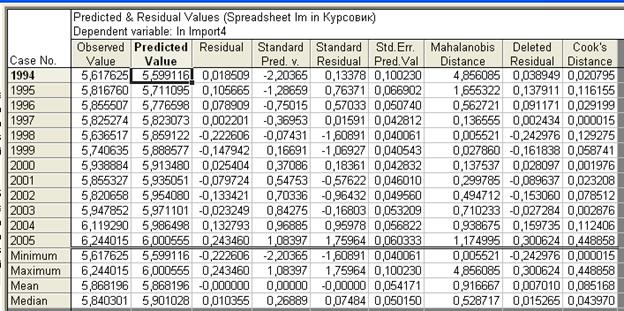
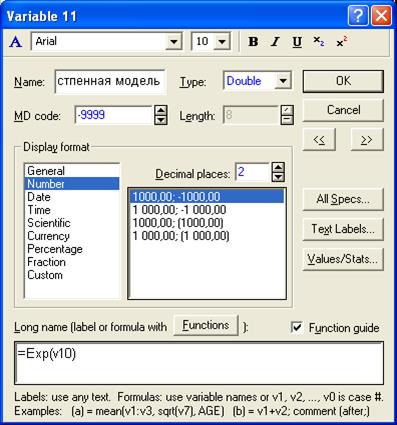
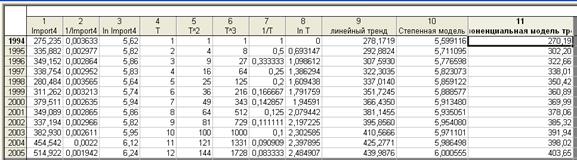

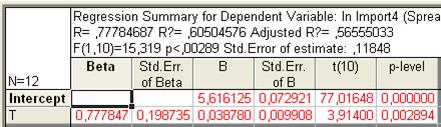



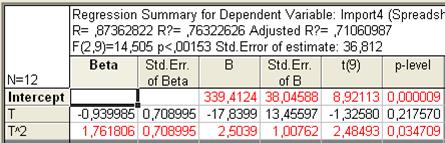
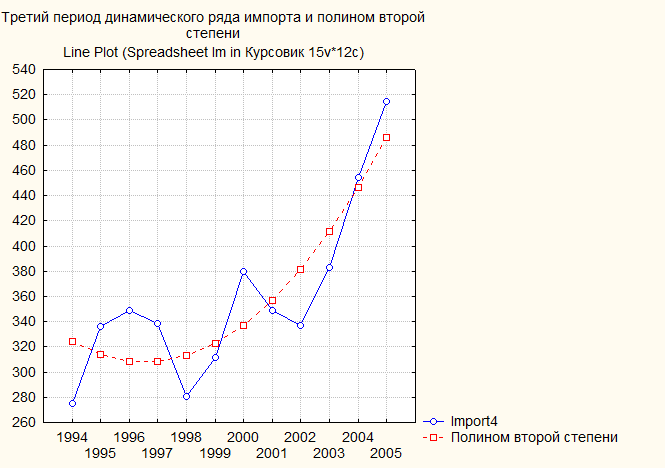
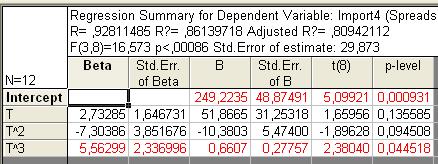
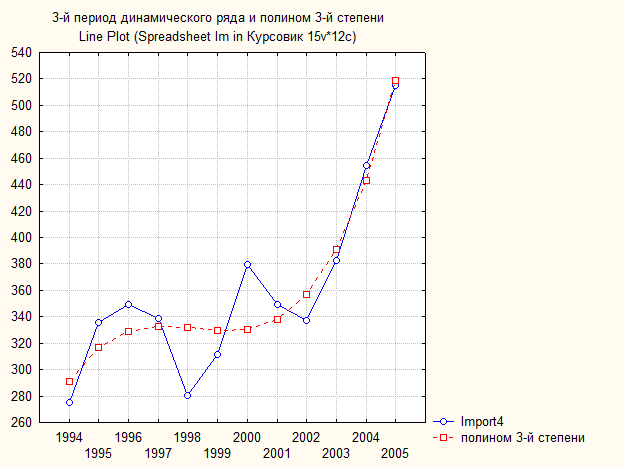
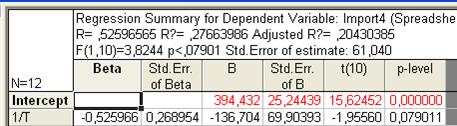

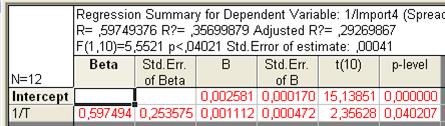
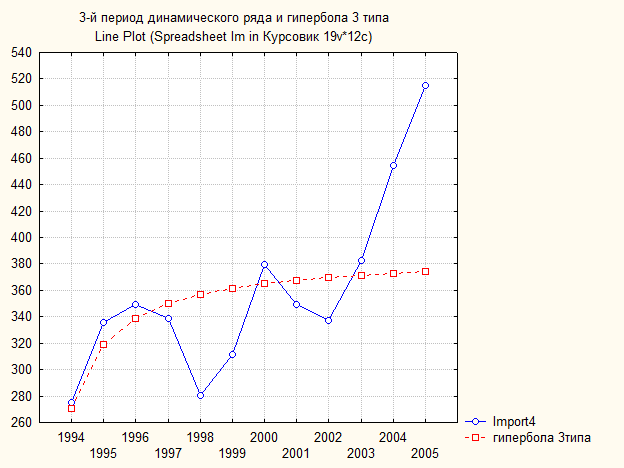

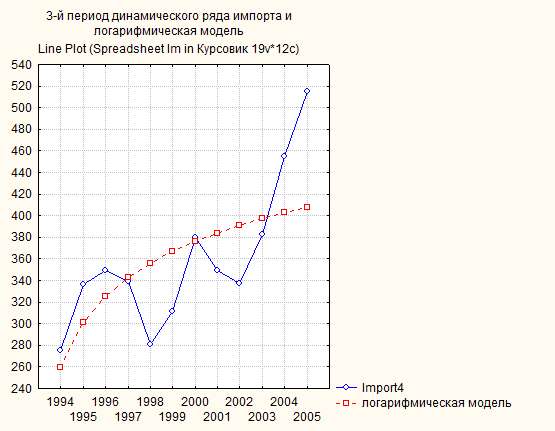

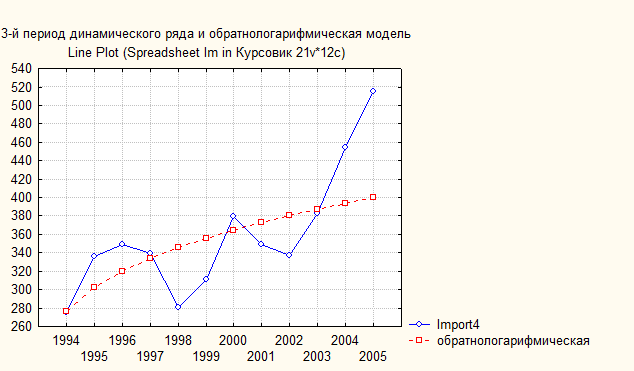
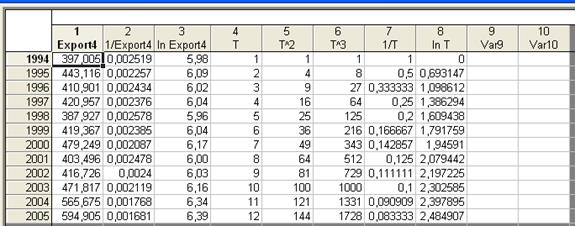


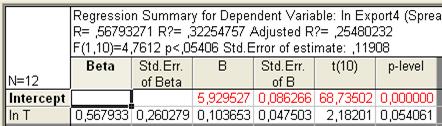
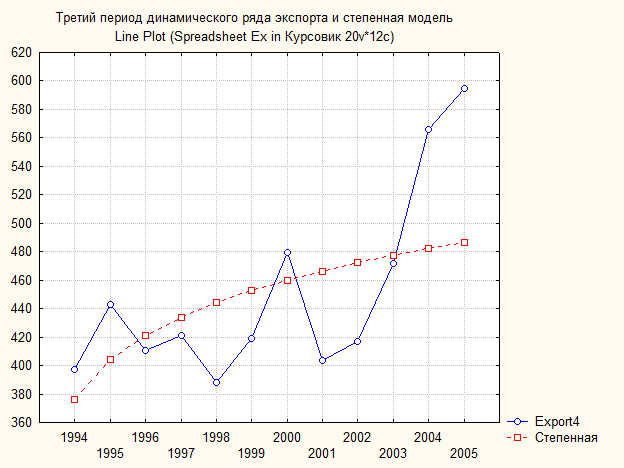

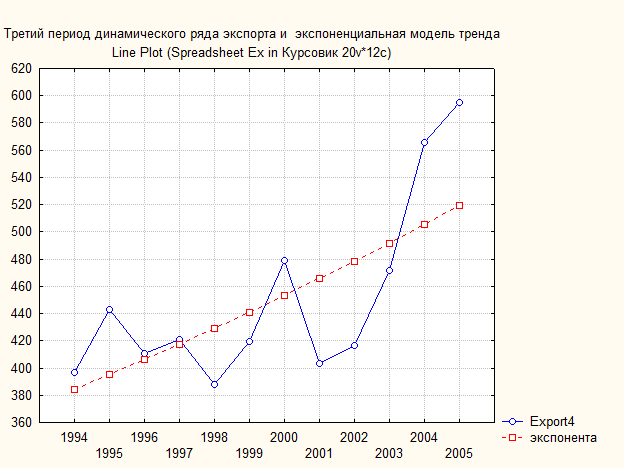
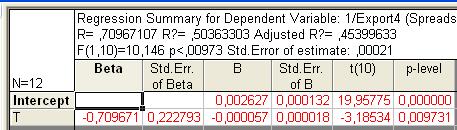
 Рис. 80. Третий период динамического ряда экспорта (млрд. $) и обратная модель
Рис. 80. Третий период динамического ряда экспорта (млрд. $) и обратная модель


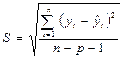 ,
,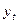 - фактические уровни ряда динамики;
- фактические уровни ряда динамики; - уровни ряда, определенные по уравнению тренда;
- уровни ряда, определенные по уравнению тренда;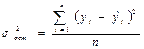
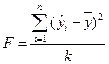 :
: 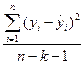 ,
, .
.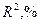

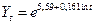
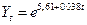
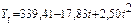
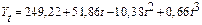
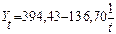
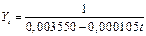
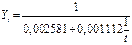
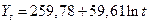
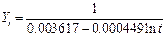
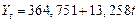

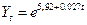
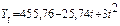
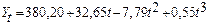
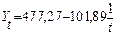
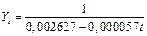
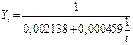
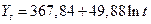
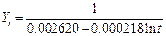
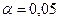 равно 3,07. Следовательно, эта модель тренда признается адекватно отражающей реальную тенденцию изучаемого явления.
равно 3,07. Следовательно, эта модель тренда признается адекватно отражающей реальную тенденцию изучаемого явления.


