Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выявление и анализ основной тенденцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Курсовой проект
по дисциплине «Статистика» на тему «Анализ динамики импорта и экспорта Англии за период с 1977 по 2006 год»»
Выполнила: студентка 3072/2 группы ________ (подпись) Широкова Т. Принял: ________ (подпись) Пономарева О.А.
«__» _______ 2008
Санкт – Петербург
Содержание Введение………………………………………………………………………...…3 1. Анализ рядов динамики ……………………………………….…………...….4 1.1 Ввод данных…………………………………………………………...…4 1.2. Графическое представление рядов динамики…………………..….…5 1.3. Показатели изменения уровней динамического ряда…………….…..7 2. Средние показатели динамики………………………………………….27 Выявление и анализ основной тенденции временного ряда………………………………………………………………….36 2.1 Компоненты ряда динамики………………………………...…………36 3. Аналитическое сглаживание временного ряда. Уравнение тренда…………………………………………………….43 3.1. Наложение оптимальных моделей тренда на исходные ряды динамики экспорта и импорта………………………………………………..…87 4. Автокорреляция в динамических рядах. Авторегрессионные модели...….89 5. Корреляция рядов динамики…………………………………………………95 6. Экстраполяция трендов и доверительные интервалы прогноза………….100 6.1. Доверительные интервалы прогноза………………………………..103 6.2 Экстраполяция на основе среднего темпа роста…………………....109 7. Графическое представление результатов……………………………….…110 прогнозирования. Заключение………………………………………………………………….…..118 Введение Важнейшей задачей практической статистики, а также менеджеров разных уровней является построение и анализ рядов динамики. Ряд динамики – это расположенные в хронологическом порядке значения того или иного показателя, изменение которого отражает ход развития изучаемого явления. Ряд динамики (временной ряд, хронологический ряд) состоит из двух элементов: моменты или периоды времени (годы, кварталы, месяцы), к которым относятся статистические данные, и сами данные, называемые уровнями ряда. Общепринятое формальное представление динамического ряда: y1, y2,..., yt,..., yn где yt ¾уровень ряра, численное значение показателя в момент (период) времени t; n ¾ число уровней ряда. Процесс развития социально-экономических явлений во времени заключается главным образом в том, что происходит изменение воздействия на них многих факторов социального, экономического, технического и другого порядка. Время, таким образом, становится собирательным фактором, вмещающим в себя многие факторы развития. Экономические явления, как и все другие явления общественной жизни, с течением времени изменяются под влиянием внутренних причин, но с внешней стороны это проявляется как результат воздействия времени. Построение и анализ рядов динамики позволяют выявить закономерности развития явлений общественной жизни и его особенности. Средние показатели динамики
Как уже отмечалось, средние показатели необходимы для получения обобщающих оценок изменения уровней временного ряда. Часто использование средних показателей становится просто необходимым. Например, сельскохозяйственное производство в огромной степени зависит от погодных условий конкретного года, и сравнение годовых показателей становится нецелесообразным. Правильнее сравнивать среднегодовые уровни, среднегодовые абсолютные приросты и темпы роста, рассчитанные за несколько лет. При сравнительном анализе изменения тех или иных показателей по разным странам, регионам или, например, при сопоставлении темпов роста заработной платы и производительности труда также целесообразно использовать средние показатели рядов динамики. Анализируя временные ряды, можно рассчитать средний уровень ряда, средний абсолютный прирост и средний темп роста (средний темп прироста определяется на основании темпа роста). Средний уровень ряда рассчитывается по-разному для моментных и интервальных рядов динамики. Средний уровень интервального ряда вычисляется по формуле средней арифметической простой:
Если отдельные периоды интервального ряда динамики имеют неодинаковую длину, то для определения среднего уровня следует воспользоваться средней арифметической взвешенной. Для неполных интервальных рядов иногда определяют полусумму уровней на начало и конец периода и принимают ее за характеристику среднего уровня всего периода. Но этот средний уровень является грубой оценкой и применяется редко. Средний уровень моментного ряда определяется по формуле, получившей название средней хронологической:
В знаменателе формулы - число уровней без единицы, поскольку в числителе первый и последний уровни берутся в половинном размере. Для неполных моментных рядов динамики применяется взвешивание сумм каждой смежной пары уровней по продолжительности периода между ними, т. е.
где t1 ¾ время (в соответствующих единицах) между моментом регистрации у1 и моментом регистрации у2; t2 — время между моментом регистрации y2 и y3 и т.д. В знаменателе берется удвоенная сумма периодов, поскольку каждое слагаемое числителя суммируется два раза. Обобщающим показателем скорости изменения явления во времени служит средний абсолютный прирост – среднее значение цепных абсолютных приростов за равные промежутки времени. Если абсолютные приросты обозначить через D1, D2, D3,..., то средний абсолютный прирост, обозначаемый через
где п - 1 — число цепных показателей абсолютного прироста за период. Так как SDt равна разности между последним и первым уровнями уп ‑ у1, то средний абсолютный прирост можно найти по формуле:
При исчислении среднего темпа роста нужно учитывать, что интенсивность развития явлений идет по правилам сложных процентов, где накладывается прирост на прирост. Поэтому средний темп роста принято вычислять по формуле средней геометрической на основании цепных темпов роста. Если через Tp1, Tp2, Tp3,..., Тр обозначить цепные темпы роста за равные промежутки, то средний темп роста выразится формулой:
где Тр — средний темп роста; n-1 — число темпов роста. Поскольку цепной темп роста является отношением последующего уровня ряда к непосредственно предшествующему, так что
Следовательно, средний темп роста может быть представлен формулой:
где п ¾ число уровней; уп ¾ уровень последнего года (периода); у1 ¾ уровень первого года (периода).
Формула средней геометрической взвешенной в общем виде будет иметь вид:
где t ¾ интервал времени, в течение которого сохранялся данный темп роста; St ¾ сумма отрезков времени.
При использовании логарифмов для вычисления средних темпов роста не надо забывать о том, что логарифмы величин, меньших единицы (но положительных), имеют отрицательную характеристику. Для расчета средних темпов прироста пользуются уже известным соотношением: Интерпретация всех выше описанных показателей обязательно должна сопровождаться указанием временного отрезка, за который рассчитана характеристика, а также единицы времени, которая является его единицей измерения, например: среднегодовой абсолютный прирост численности населения за 20 лет; среднемесячный темп роста объема продаж за 10 лет и т. п. Рассмотрим алгоритм расчета описанных выше показателей в STATISTICA. Выбираем меню Statistics/Nonparametrics. Также эти показатели можно получить с помощью меню Statistics/Basic Statistics/Tables/Descriptive Statistics (см. пособие «Методы анализа распределений. Выборочное наблюдение»). В появившемся диалоговом окне выбираем пункт Ordinal descriptive statistics (median, mode,…) – обычные описательные статистики.
Рис.27 Меню Nonparametric Statistics
В появившемся окне сначала выбираем переменные, нас интересует средние показатели по ряду динамики в общем, а так же показатели четвертого периода. Поэтому выбираем следующие переменные Import – исходные данные, APRC – абсолютный прирост, TRC – цепные темпы роста, TPRC – цепные темпы прироста. Следует повторить процедуру и для Export. Для вычисления показателей по четвертому периоду необходимо создать дополнительные переменные, содержащие показатели изменений уровней динамического ряда за последний год. Далее нажимаем кнопку Summary: Ordinal descriptive statistics. Это приводит к вычислению разнообразных статистик, включая нужные нам: геометрическую среднею (для расчета среднего коэффициента роста) и среднею арифметическую (для расчета среднего уровня за период и среднего абсолютного прироста). Появляется расчетная таблица, для того чтобы привести ее к удобному для анализа виду необходимо транспонировать матрицу. Для этого выбираем меню Data/Transpose/File.
Рис.28 Результат расчета параметров для импорта
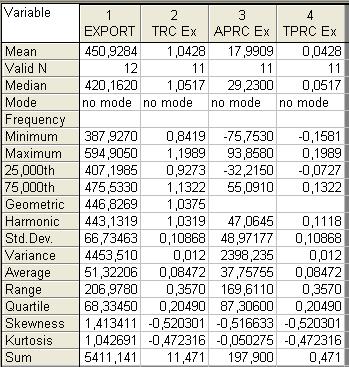
Рис.29 Результат расчета параметров для экспорта
В данной таблице Mean – средняя арифметическая, этот показатель используется для нахождения среднего уровня ряда и определения среднего абсолютного прироста(APRC). Для определения среднего темпа роста используется показатель геометрической средней - Geometric (столбец TRC). Для нахождения среднего темпа прироста из последнего показателя вычитаем единицу. Результаты рассчитанных выше показателей, а также результаты показателей рассчитанных в предыдущих пунктах приведены в таблицах ниже. Для третьего периода рассчитаем отдельно все показатели и построим гравики.
Посчитаем основные параметры для третьего периода.
Рис. 30. Исходные данные за третий период с рассчитанными для низ показателями
Рис. 31. Результат расчета параметров для импорта
Рис. 32. Результат расчета параметров для экспорта
Таблица 2. Расчет показателей Import
Таблица 3. Расчет показателей Export
Временного ряда. Компоненты ряда динамики Одной из важнейших задач статистического анализа рядов динамики является выявление и описание основной тенденции развития изучаемого явления, закономерности изменения уровней ряда. Иногда характер тенденции достаточно отчетливо проявляется на графике и в системе статистических показателей, описанных в предыдущих параграфах. Однако часто встречаются динамические ряды, в которых основная тенденция не является очевидной, поскольку на уровни ряда влияет большое число разнообразных факторов. Основная тенденция развития того или иного явления складывается под воздействием долговременно действующих внутренних и внешних причин и условий, благодаря которым, в основном, формируется величина уровня ряда. Одновременно с этим, уровни динамического ряда колеблются (отклоняются от основной тенденции) под воздействием краткосрочных случайных или систематически (циклически) действующих факторов. Чем сильнее их влияние, тем сложнее вскрыть основную закономерность развития объекта. При анализе рядов динамики могут быть выделены четыре компоненты, формирующие уровни:
где T - главная компонента, отражающая основную тенденцию развития, так называемый тренд; C – циклическая (конъюнктурная) компонента; S – сезонная компонента; e – случайная компонента. В зависимости от взаимосвязи выделяемых компонент модель временного ряда может быть аддитивная:
либо мультипликативная:
Мультипликативная модель легко приводится к линейному виду путем логарифмирования. Выделение и изучение отдельных компонент временного ряда называется декомпозицией ряда динамики. Изучение каждой компоненты предполагает использование специальных приемов и методов. Все названные компоненты содержит далеко не любой динамический ряд. Чаще всего в практических исследованиях встречаются ряды, содержащие трендовую и случайную компоненты. Чтобы видеть влияние сезонной составляющей, нужно иметь ряд, уровни которого относятся к месяцам или кварталам. Проявление циклической компоненты, как правило, характерно для больших динамических рядов, что связано с экономическими (бизнес) циклами. Чем меньше влияние на уровни ряда нетрендовых компонент, тем проще выделить тренд – основную тенденцию изучаемого ряде, описание и прогнозирование которой является центральной задачей изучения временных рядов. Тенденция – это объективно существующее свойство того или иного процесса, которое лишь приближенно описывается трендом определенного вида. Трендом называют и саму основную тенденцию развития, и конкретное ее описание с помощью уравнения регрессии. Для выявления и анализа общей тенденции развития изучаемого явления необходимо абстрагироваться от влияния нетрендовых факторов. Достичь этого, в определенной степени, позволяют приемы сглаживания или выравнивания временного ряда. Различают механическое и аналитическое выравнивания. Последнее позволяет формализовать тенденцию, представить ее в виде конкретной математической функции. Суть различных приемов, с помощью которых осуществляется сглаживание, сводится к замене фактических уровней динамического ряда расчетными, имеющими значительно меньшую колеблемость, чем исходные данные. Уменьшение колеблемости уровней позволяет тенденции развития проявиться более отчетливо. В ряде случаев сглаживание ряда может рассматриваться как важное вспомогательное средство, облегчающее применение других методов и, в частности, более строгих методов выделения тенденции.
Ряда. Уравнение тренда. Кривые роста, описывающие закономерности развития явлений во времени, - это результат аналитического выравнивания динамических рядов. Выравнивание ряда с помощью тех или иных функций (т. е. их подгонка к данным) в большинстве случаев оказывается удобным средством описания эмпирических данных. Это средство при соблюдении ряда условий можно применить и для прогнозирования. Процесс выравнивания состоит из следующих основных этапов: - выбора типа кривой, форма которой соответствует характеру изменения динамического ряда; - определения численных значений (оценивание) параметров кривой; - апостериорного контроля качества выбранного тренда. В современных ППП все перечисленные этапы реализуются одновременно, как правило, в рамках одной процедуры. Аналитическое сглаживание с использованием той или иной функции позволяет получить выравненные, или, как их иногда не вполне правомерно называют, теоретические значения уровней динамического ряда, т. е. те уровни, которые наблюдались бы, если бы динамика явления полностью совпадала с кривой. Эта же функция с некоторой корректировкой или без нее, применяется в качестве модели для экстраполяции (прогноза). Вопрос о выборе типа кривой является основным при выравнивании ряда. При всех прочих равных условиях ошибка в решении этого вопроса оказывается более значимой по своим последствиям (особенно для прогнозирования), чем ошибка, связанная со статистическим оцениванием параметров. Поскольку форма тренда объективно существует, то при выявлении ее следует исходить из материальной природы изучаемого явления, исследуя внутренние причины его развития, а также внешние условия и факторы на него влияющие. Только после глубокого содержательного анализа можно переходить к использованию специальных приемов, разработанных статистикой. Весьма распространенным приемом выявления формы тренда является графическое изображение временного ряда. Но при этом велико влияние субъективного фактора, даже при отображении выровненных уровней. Наиболее надежные методы выбора уравнения тренда основаны на свойствах различных кривых, применяемых при аналитическом выравнивании. Такой подход позволяет увязать тип тренда с теми или иными качественными свойствами развития явления. Нам представляется, что в большинстве случаев практически приемлемым является метод, который основывается на сравнении характеристик изменения приростов исследуемого динамического ряда с соответствующими характеристиками кривых роста. Для выравнивания выбирается та кривая, закон изменения прироста которой наиболее близок к закономерности изменения фактических данных. В табл. 4 приводится перечень наиболее употребительных при анализе экономических рядов видов кривых и указываются соответствующие «симптомы», по которым можно определить, какой вид кривых подходит для выравнивания. При выборе формы кривой надо иметь в виду еще одно обстоятельство. Рост сложности кривой в целом ряде случаев может действительно увеличить точность описания тренда в прошлом, однако в связи с тем, что более сложные кривые содержат большее число параметров и более высокие степени независимой переменной, их доверительные интервалы будут в общем существенно шире, чем у более простых кривых при одном и том же периоде упреждения. Таблица 4 Характер изменения показателей, основанных
В настоящее время, когда использование специальных программ без особых усилий позволяет одновременно строить несколько видов уравнений, широко эксплуатируются формальные статистические критерии для определения лучшего уравнения тренда. Из сказанного выше, по-видимому, можно сделать вывод о том, что выбор формы кривой для выравнивания представляет собой задачу, которая не решается однозначно, а сводится к получению ряда альтернатив. Окончательный выбор не может лежать в области формального анализа, тем более, если предполагается с помощью выравнивания не только статистически описать закономерность поведения уровня в прошлом, но и экстраполировать найденную закономерность в будущее. Вместе с тем различные статистические приемы обработки данных наблюдения могут принести существенную пользу, по крайней мере, с их помощью можно отвергнуть заведомо непригодные варианты и тем самым существенно ограничить поле выбора. Рассмотрим наиболее используемые типы уравнений тренда: 1.Линейная форма тренда:
где
Для линейной формы тренда характерно равенство так называемых первых разностей (абсолютных приростов) и нулевые вторые разности, т. е. ускорения. 2.Параболическая (полином 2-ой степени) форма тренда:
Для данного типа кривой постоянными являются вторые разности (ускорение), а нулевыми – третьи разности. Параболическая форма тренда соответствует ускоренному или замедленному изменению уровней ряда с постоянным ускорением. Если 3.Экспоненциальная форма тренда:
где При 4.Гиперболическая форма тренда (1 типа):
Данная форма тренда может отображать тенденцию процессов, ограниченных предельным значением уровня. 5.Логарифмическая форма тренда:
где Логарифмическим трендом может быть описана тенденция, проявляющаяся в замедлении роста уровней ряда динамики при отсутствии предельно возможного значения. При достаточно большом t логарифмическая кривая становится мало отличимой от прямой линии. 6.Обратнологарифмическая форма тренда:
7.Мультипликативная (степенная) форма тренда:
8.Обратная (гиперболическая 2 типа) форма тренда:
9.Гиперболическая форма тренда 3 типа:
10.Полином 3-ей степени:
Для всех нелинейных, относительно исходных переменных моделей (уравнений регрессии), а их здесь большинство, требуется провести вспомогательные преобразования, представленные в таблице ниже. Таблица 5 Модели, сводящиеся к линейному тренду
В формулах, перечисленных в таблице, как и во всех формулах, описывающих модель тренда, Однако, при практическом использовании линеаризации с помощью преобразования исследуемых переменных следует иметь ввиду, что оценки параметров, полученных линеаризацией с помощью М.Н.К. (метод наименьших квадратов), минимизируют сумму квадратов отклонений для преобразованных, а не исходных переменных. Поэтому полученные с помощью линеаризации зависимостей оценки нуждаются в уточнении. Для решения поставленной задачи по аналитическому сглаживанию динамических рядов в системе STATISTICA нам потребуется создать несколько новых дополнительных переменных, необходимых для выполнения дальнейшей работы, а также осуществить некоторые вспомогательные операции по преобразованию нелинейных моделей тренда в линейные. Итак, нам предстоит построить уравнение тренда, которое по существу является уравнением регрессии, в котором в качестве фактора выступает «время». Прежде всего, мы создадим переменную «Т», содержащую моменты времени четвертого периода. Так как четвертый период включает 12 лет, то переменная «Т» будет состоять из натуральных чисел от 1 до 12, соответствующих месяцам года. Кроме того, для работы с некоторыми моделями тренда нам потребуется еще несколько переменных, содержание которых можно понять из их обозначения. Это переменные, получаемые из временного ряда: «Т^2», «Т^3», «1/Т» и «ln T». А также переменные, получаемые из исходных данных за четвертый период: «1/Import4» и «ln Import4». Также необходимо создать такую же таблицу для экспорта. Все это предлагается сделать на новом рабочем листе, скопировав туда данные за 4-й период. Для этого воспользуемся уже известным нам меню Workbook/Insert. В итоге получаем следующие электронные таблицы.
Рис. 38. Таблица со вспомогательными переменными для импорта
Рис. 39. Таблица со вспомогательными переменными для экспорта
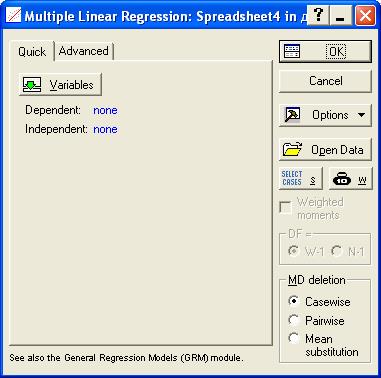
Для аналитического выравнивания рядов динамики мы будем использовать модуль Multiple Regression в меню Statistics. Рассмотрим пример построения графического изображения и определение численных параметров тренда, выраженного линейной зависимостью.
Рис. 40. Модуль Multiple Regression в меню Statistics
Для выбора зависимых и независимых переменных воспользуемся кнопкой Variables. В открывшемся окне в левом информационном поле мы выбираем зависимую переменную Yt, (в нашем случае это Import 4 – данные по четвертому периоду). Номера выбранных зависимых переменных отображаются внизу в поле Dependent var. (or list for batch). Соответственно в правом поле мы выбираем независимые переменные (в нашем случае одну – время «Т»). Номера выбранных независимых переменных высвечиваются внизу в поле Independent variable list. После того, как завершен выбор переменных, нажимаем ОК. Система выдает окно с обобщенными результатами расчета параметров тренда (далее они будут рассмотрены более подробно) и возможностью выбора направления для последующего детального анализа. Заметим, что значение оценки, высвеченное красным цветом, указывает на статистическую значимость результатов. Далее переходим к закладке Advanced.
Рис. 41. Закладка Advanced
На закладке располагается несколько кнопок, позволяющих получить максимально детализированные сведения по интересующему нас направлению анализа. При нажатии на нее получаем две таблицы с результатами регрессионного анализа. В первой представлены результаты расчета параметров уравнения регрессии, во второй – основные показатели уравнения.
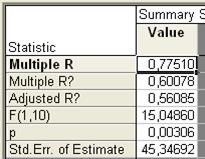
Рис. 42. Основные показатели уравнения для данных импорта за четвертый период (линейный тренд) Здесь N = – объем результативной переменной. В верхнем поле расположены показатели R,
Рис. 43. Параметры уравнения регрессии для данных импорта за четвертый период (линейный тренд)
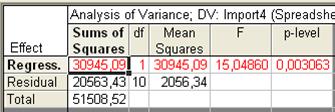
Для оценки статистической значимости уравнения в целом на закладке Advanced воспользуемся кнопкой ANOVA (Goodness Of Fit), позволяющей получить таблицу дисперсионного анализа и значение F-критерия Фишера.
Рис. 44. Таблица дисперсионного анализа
&
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 885; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.13.192 (0.013 с.) |


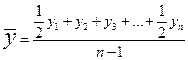
 ,
, , может быть найден по формуле:
, может быть найден по формуле: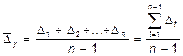 ,
,
 ,
,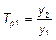 ;
;  ,..., в формуле средней геометрической подкоренное выражение преобразуется:
,..., в формуле средней геометрической подкоренное выражение преобразуется: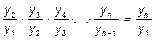
 ,
, ,
,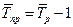 (в виде коэффициентов) и
(в виде коэффициентов) и  .
.




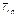

 ,
, ,
,

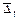
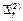
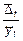
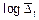
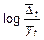
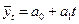 ,
,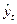 - уровень ряда, полученный в результате выравнивания по прямой;
- уровень ряда, полученный в результате выравнивания по прямой; - начальный уровень тренда;
- начальный уровень тренда; - средний абсолютный прирост; константа тренда.
- средний абсолютный прирост; константа тренда.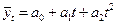
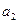 < 0 и
< 0 и 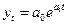 ,
,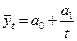
 ,
,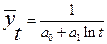
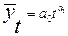
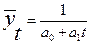

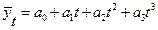
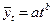
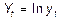
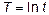
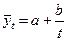
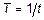
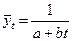
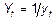
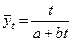
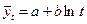
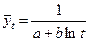
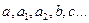 есть коэффициенты уравнений.
есть коэффициенты уравнений.

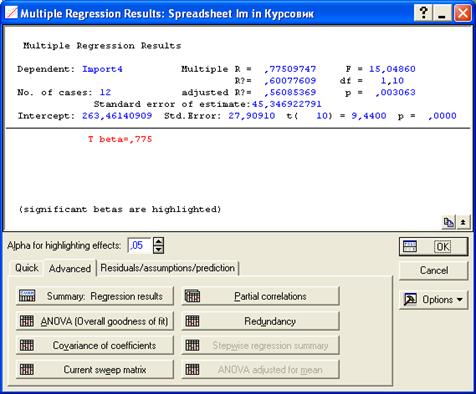
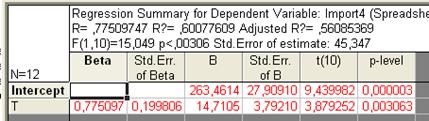
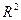 , Adjusted R, F, p, Std.Error of Estimate, означающие соответственно теоретическое корреляционное отношение, коэффициент детерминации, уточненный коэффициент детерминации, расчетное значение критерия Фишера (в скобках дано число степеней свободы), уровень значимости, стандартная ошибка уравнения (эти же показатели можно увидеть во второй таблице). В самой таблице нас интересуют столбец В, в котором расположены коэффициенты уравнения, столбец t и столбец p-level, обозначающие расчетное значение t-критерия и расчетный уровень значимости, необходимые для оценки значимости параметров уравнения. При этом система помогает пользователю: когда процедура предполагает проверку на значимость, STATISTICA выделяет значимые элементы красным цветом (т.е. отвергается нулевая гипотеза о равенстве параметров нулю). В нашем случае |tфакт| > tтабл для обоих параметров, следовательно они значимы.
, Adjusted R, F, p, Std.Error of Estimate, означающие соответственно теоретическое корреляционное отношение, коэффициент детерминации, уточненный коэффициент детерминации, расчетное значение критерия Фишера (в скобках дано число степеней свободы), уровень значимости, стандартная ошибка уравнения (эти же показатели можно увидеть во второй таблице). В самой таблице нас интересуют столбец В, в котором расположены коэффициенты уравнения, столбец t и столбец p-level, обозначающие расчетное значение t-критерия и расчетный уровень значимости, необходимые для оценки значимости параметров уравнения. При этом система помогает пользователю: когда процедура предполагает проверку на значимость, STATISTICA выделяет значимые элементы красным цветом (т.е. отвергается нулевая гипотеза о равенстве параметров нулю). В нашем случае |tфакт| > tтабл для обоих параметров, следовательно они значимы.