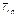Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Показатели изменения уровней динамического рядаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Анализ динамических рядов социально-экономических явлений обычно начинают с рассмотрения статистик, расчет которых не требует какой-либо предварительной обработки анализируемого динамического ряда. Речь идет о так называемых показателях динамического ряда, позволяющих пояснить характер, скорость, интенсивность и направление развития изучаемого явления за определенный временной период. В результате того или иного сопоставления уровней динамического ряда формируется система абсолютных и относительных показателей динамики, к числу которых относятся абсолютные приросты (и их среднее значение), ускорение, коэффициенты роста (и их среднее значение), коэффициенты прироста (и их среднее значение), абсолютное значение одного процента прироста. Сравниваемый уровень динамического ряда называется текущим, а уровень, с которым производится сравнение, базисным. В зависимости от того, что принимается за базу сравнения будут получены различные показатели динамики. Приняв за базу сравнения некоторый постоянный уровень, например y 1 получим серию базисных показателей, которые характеризуют окончательный результат всех изменений в уровнях ряда от первого периода (или момента времени) до текущего периода. Следует иметь ввиду, что в реальных задачах за базу сравнения может быть принят уровень ряда, относящийся к периоду (моменту), выходящему за пределы анализируемого динамического ряда (например, начальный момент периода с которого начинается некоторый новый этап развития). Если производится сравнение текущего уровня (yt) с непосредственно предшествующим (yt- 1), то получаются цепные показатели динамики. Абсолютным приростом называется разность между значениями уровней данного периода и предшествующего (либо базисного):
где yt — уровень ряда динамики в момент времени t; yt-1 — уровень ряда динамики в момент времени t -1; D t — абсолютный прирост. За весь период, описываемый временным рядом, абсолютный прирост (D) выразится как алгебраическая сумма частных цепных приростов или, что очевидно, как разность между последним и первым уровнями:
где yn ¾ последний уровень ряда; у 1 ¾ первый уровень. Абсолютный прирост может быть как положительным, так и отрицательным. Он показывает, насколько уровень текущего периода выше или ниже предшествующего и выражает абсолютную скорость роста или снижения уровней ряда. Абсолютные изменения уровней динамического ряда могут быть примерно одинаковы, т. е. выступать константой тенденции развития явления. Но если величина абсолютного прироста со временем возрастает, это означает, что уровни ряда изменяются с ускорением. Ускорение – это разность между последующим и предыдущим абсолютными приростами.
При расчете характеристики ускорения, сопоставляемые временные отрезки должны быть одинаковы, а показатель может быть рассчитан только на основе цепных абсолютных приростов. Ускорение – это скорость изменения скорости (так называемые вторые разности). Отрицательное значение ускорения говорит о замедлении скорости роста уровней ряда или об ускорении скорости их снижения. Темпом роста (коэффициентом роста) - это отношение последующего уровня к предыдущему или какому-либо другому, принятому за базу сравнения. Темп роста оценивает, во сколько раз уровень текущего периода выше или ниже уровня базисного периода, или сколько процентов он составляет по отношению к базисному. Таким образом, темп роста может быть представлен в виде коэффициента, когда определяется непосредственное отношение абсолютных размеров уровней, и в процентах к базисному уровню, принятому за 100%. Темп роста в виде коэффициентов вычисляется по формулам:
где yconst – база сравнения;
Величина темпа роста больше единицы показывает увеличение уровня текущего периода по сравнению с базисным. Величина темпа роста, равная единице, показывает, что уровень текущего периода по сравнению с базисным не изменился, меньше единицы - уменьшение уровня текущего периода. Темп роста всегда имеет положительный знак. Цепные темпы роста характеризуют интенсивность изменения уровней ряда. Темпом прироста - это отношение абсолютного прироста к базе сравнения, т. е.
где D t ¾ абсолютный прирост данного уровня; yt-1 — базисный уровень (уровень предыдущего периода); Tnp — темп прироста (в виде коэффициента). Этот показатель характеризует относительную скорость изменения уровня ряда в единицу времени. Темп прироста, выраженный в процентах, показывает на сколько процентов увеличился или уменьшился текущий уровень по сравнению с базисным, принятым за 100%, или, иначе, сколько процентов составляет абсолютный прирост данного уровня по отношению к базисному уровню. Поскольку абсолютный прирост (D) за весь период равен уп - у 1, то темп прироста за весь период составит:
а При темпах роста, меньше 100% или единицы (уменьшение уровней ряда), получаем отрицательные темпы прироста, т.е. темпы снижения. Следующая статистическая характеристика динамики, основанная на измерении соотношений уровней, называется абсолютным значением одного процента прироста. Абсолютное значение одного процента прироста показывает, какая абсолютная величина скрывается за относительным показателем — одним процентом прироста. Оно представляет собой отношение величины абсолютного прироста к темпу прироста, выраженному в процентах.
Следовательно, абсолютное значение одного процента прироста можно вычислить как 0,01 от базисного (предшествующего) уровня. Этот показатель имеет большое значение в экономическом анализе, поскольку темпы роста могут иметь тенденцию к уменьшению или оставаться на одном уровне, а абсолютное значение одного процента прироста расти. Рассмотрим алгоритм расчета вышеописанных показателей в системе STATISTICA. Для этого потребуется произвести некоторые дополнительные преобразования имеющихся переменных. В разделе главного меню Statistics выбираем подменю Advanced Linear/Nonlinear Models и в нем команду Time Series/Forecasting. Открывается модуль, в котором реализованы практически все современные методы анализа и прогнозирования, и который будет постоянно использоваться при выполнении курсового проекта.
Рис.6 Модуль анализа и прогнозирования
Рассмотрим рабочую область данного модуля: 1. В верхней части панели, в информационном поле записываются имена анализируемых и преобразованных переменных. Рядом с информационным полем расположены стандартные кнопки системы (Cancel, Options). Сверху от информационного поля уже известная нам кнопка Variables для выбора переменных и кнопка ОК (transformations, autocorrelations, crosscorrelations, plots). 2. Нижняя часть панели (под пояснительным текстом) - функциональная. На закладке Quick расположены кнопки, открывающие специальные диалоговые окна анализа, а закладка Missing Data содержит опции обработки пропущенных значений. Как и всегда начинаем работу с выбора переменных – нажимаем кнопку Variables и выбираем интересующую нас переменные Import, Export (с удаленными данными последних двух периодов). После выбора переменной для анализа в информационном поле появляются ее имя, слева - значок «L» в графе Lock, который означает, что выбранные переменные являются закрытыми на «ключ» и не могут быть удалены без прерывания анализа. Дальнейшая работа происходит именно с этими переменными, которые можно преобразовывать, анализировать, трансформировать, но нельзя удалять из текущего анализа. В процессе работы динамические ряды подвергаются многократному преобразованию. Однако, не все результаты этих преобразований необходимы в работе. Кнопка Delete highlighted variable позволяет удалять из диалогового окна лишнюю информацию (выделенную переменную). Напротив, некоторые переменные используются для дальнейшего анализа и их необходимо сохранять (кнопка Save variables). Для расчета цепных показателей изменения уровней динамического ряда необходимо иметь две переменные: первая переменная – исходный динамический ряд, состоящий из уровней сравниваемых периодов yt, а вторая переменная – динамический ряд, состоящий из уровней непосредственно предшествующих периодов yt-1, т.е. база сравнения.Очевидно, что первые переменные у нас имеется, для получения вторых переменных нажмем на кнопку ОК (transformations, autocorrelations, crosscorrelations, plots), открывающую диалоговое окно преобразования переменных Transformations Of Variables. Выбираем закладку Shift и ставим метку в поле Shift (Lag) Series Back с числом лагов 1, так как мы хотим получить временной ряд, смещенный относительно исходного на один временной период (лаг). Далее нажимаем кнопку ОК (Transform Selected Series). Система автоматически строит график полученного динамического ряда, а в информационном поле диалогового окна в графе Variables появляется преобразованная переменная. После этого нажимаем на кнопку Save variables для сохранения результатов преобразования. Результаты сохраняются в отдельной электронной таблице в виде двух переменных. Во избежание потери данных предлагается поместить данную таблицу в исходную рабочую книгу путем нажатия на кнопку Add to Workbook и выбором соответствующей рабочей книги.
После того как получены необходимые для дальнейших вычислений переменные, можно приступать непосредственно к расчету показателей динамики. В качестве примера рассмотрим процедуру расчета цепных темпов роста для динамических рядов. Для этого на вновь полученном рабочем листе уже известным нам способом (см. выше) создадим новую переменную, в которой будут рассчитаны цепные темпы роста (TRC). Сначала выберем формат переменной – нас интересует числовой (значит в поле Display Format выбираем Number). Система позволяет вводить в электронные таблицы новые данные, на основе имеющихся, путем вычислений с использованием формул, которые задаются в поле Long Name (Label Or Formula With Functions). Система воспринимает все математические операторы, таким же образом, как и другие Windows-приложения. Пробелов между элементами уравнения ставить не надо. В формулу можно вводить и численные значения и функции, полный набор которых вызывается кнопкой Function или автоматически раскрывается при вводе первой буквы соответствующей функции. Условием получения новых данных является постановка знака равенства перед любой формулой. Переменные в системе вводятся в следующем формате: любая переменная обозначается буквой «v» c соответствующим номером, обозначающим порядковый номер столбца, в котором эта переменная содержится. При этом регистр буквы не важен. Важно обратить внимание, чтобы в поле Decimal places не значился ноль (что будет означать округление до целого); цифра, фиксируемая в данном поле, означает число знаков после запятой в десятичной дроби. Записываем формулу для расчета цепных темпов роста для импорта «=v3/v1», где «v1» - исходный динамический ряд, а «v3» - динамический ряд, опережающий исходный на один лаг. Далее нажимаем ОК. И при появлении следующего окна выбираем «Да». Это означает подтверждение расчета новой переменной и согласие с тем, что в случае невозможности расчета каких-либо ячеек, они будут оставлены пустыми.
Рис.7 Запрос системы
Рис.8 Расчет TRC
В итоге получается новый столбец с рассчитанными цепными темпами роста. Естественно, что первая и последняя его ячейка будут пустыми, так как в первом случае отсутствует делитель, а во втором делимое. Теперь рассмотрим формулу для построения базисных темпов роста, здесь в качестве знаменателя дроби будет использоваться численное значение первого уровня динамического ряда. С тем, чтобы показатели изменения уровней динамического ряда не были сдвинуты относительно друг друга, базисные показатели следует рассчитывать на основе опережающего ряда.
Рис.9 Расчет TRB
Далее представим формулы соответственно для абсолютных цепных и базисных приростов и абсолютных и базисных темпов прироста.
Рис.10 Расчет APRC
Рис.11 Расчет APRB
Рис.12 Расчет TPRC
Рис.13 Расчет TPRB
Далее можно перенести столбцы с показателями в исходную таблицу, где в качестве временной оси уже вбиты интересующие нас периоды. В итоге получается следующая таблица.
Таблица 1. Исходная таблица со столбцами показателей
Все рассчитанные показатели могут быть представлены графически. Для этого воспользуемся процедурой построения графиков, рассмотренной ранее.
Рис.14 Графическое представление показателя APRC для импорта
Рис.15 Графическое представление показателя APRC для экспорта
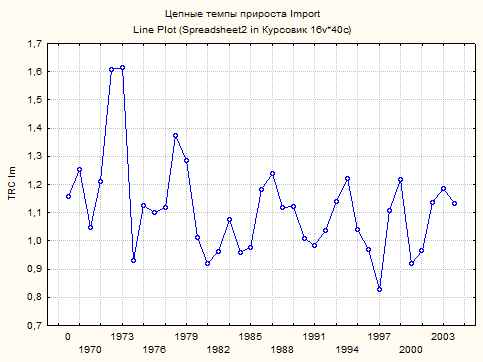
Рис.16 Графическое представление показателя TRC для импорта
Рис.17 Графическое представление показателя TRC для экспорта
Рис.18 Графическое представление показателя TRB для импорта
Рис.19 Графическое представление показателя TRB для экспорта
Рис.20 Графическое представление показателя TPRC для импорта
Рис.21 Графическое представление показателя TPRC для экспорта
Рис.22 Графическое представление показателя TPRB для импорта
Рис.23 Графическое представление показателя TPRB для экспорта
Рассчитанные абсолютные и относительные показатели динамики варьируют, изменяются во времени. Это обстоятельство вызывает необходимость расчета обобщающих характеристик, которыми являются средние показатели. Прежде чем приступить к рассмотрению методики их расчета, остановимся на понятии периодизации рядов динамики. Средние показатели динамики
Как уже отмечалось, средние показатели необходимы для получения обобщающих оценок изменения уровней временного ряда. Часто использование средних показателей становится просто необходимым. Например, сельскохозяйственное производство в огромной степени зависит от погодных условий конкретного года, и сравнение годовых показателей становится нецелесообразным. Правильнее сравнивать среднегодовые уровни, среднегодовые абсолютные приросты и темпы роста, рассчитанные за несколько лет. При сравнительном анализе изменения тех или иных показателей по разным странам, регионам или, например, при сопоставлении темпов роста заработной платы и производительности труда также целесообразно использовать средние показатели рядов динамики. Анализируя временные ряды, можно рассчитать средний уровень ряда, средний абсолютный прирост и средний темп роста (средний темп прироста определяется на основании темпа роста). Средний уровень ряда рассчитывается по-разному для моментных и интервальных рядов динамики. Средний уровень интервального ряда вычисляется по формуле средней арифметической простой:
Если отдельные периоды интервального ряда динамики имеют неодинаковую длину, то для определения среднего уровня следует воспользоваться средней арифметической взвешенной. Для неполных интервальных рядов иногда определяют полусумму уровней на начало и конец периода и принимают ее за характеристику среднего уровня всего периода. Но этот средний уровень является грубой оценкой и применяется редко. Средний уровень моментного ряда определяется по формуле, получившей название средней хронологической:
В знаменателе формулы - число уровней без единицы, поскольку в числителе первый и последний уровни берутся в половинном размере. Для неполных моментных рядов динамики применяется взвешивание сумм каждой смежной пары уровней по продолжительности периода между ними, т. е.
где t1 ¾ время (в соответствующих единицах) между моментом регистрации у1 и моментом регистрации у2; t2 — время между моментом регистрации y2 и y3 и т.д. В знаменателе берется удвоенная сумма периодов, поскольку каждое слагаемое числителя суммируется два раза. Обобщающим показателем скорости изменения явления во времени служит средний абсолютный прирост – среднее значение цепных абсолютных приростов за равные промежутки времени. Если абсолютные приросты обозначить через D1, D2, D3,..., то средний абсолютный прирост, обозначаемый через
где п - 1 — число цепных показателей абсолютного прироста за период. Так как SDt равна разности между последним и первым уровнями уп ‑ у1, то средний абсолютный прирост можно найти по формуле:
При исчислении среднего темпа роста нужно учитывать, что интенсивность развития явлений идет по правилам сложных процентов, где накладывается прирост на прирост. Поэтому средний темп роста принято вычислять по формуле средней геометрической на основании цепных темпов роста. Если через Tp1, Tp2, Tp3,..., Тр обозначить цепные темпы роста за равные промежутки, то средний темп роста выразится формулой:
где Тр — средний темп роста; n-1 — число темпов роста. Поскольку цепной темп роста является отношением последующего уровня ряда к непосредственно предшествующему, так что
Следовательно, средний темп роста может быть представлен формулой:
где п ¾ число уровней; уп ¾ уровень последнего года (периода); у1 ¾ уровень первого года (периода).
Формула средней геометрической взвешенной в общем виде будет иметь вид:
где t ¾ интервал времени, в течение которого сохранялся данный темп роста; St ¾ сумма отрезков времени.
При использовании логарифмов для вычисления средних темпов роста не надо забывать о том, что логарифмы величин, меньших единицы (но положительных), имеют отрицательную характеристику. Для расчета средних темпов прироста пользуются уже известным соотношением: Интерпретация всех выше описанных показателей обязательно должна сопровождаться указанием временного отрезка, за который рассчитана характеристика, а также единицы времени, которая является его единицей измерения, например: среднегодовой абсолютный прирост численности населения за 20 лет; среднемесячный темп роста объема продаж за 10 лет и т. п. Рассмотрим алгоритм расчета описанных выше показателей в STATISTICA. Выбираем меню Statistics/Nonparametrics. Также эти показатели можно получить с помощью меню Statistics/Basic Statistics/Tables/Descriptive Statistics (см. пособие «Методы анализа распределений. Выборочное наблюдение»). В появившемся диалоговом окне выбираем пункт Ordinal descriptive statistics (median, mode,…) – обычные описательные статистики.
Рис.27 Меню Nonparametric Statistics
В появившемся окне сначала выбираем переменные, нас интересует средние показатели по ряду динамики в общем, а так же показатели четвертого периода. Поэтому выбираем следующие переменные Import – исходные данные, APRC – абсолютный прирост, TRC – цепные темпы роста, TPRC – цепные темпы прироста. Следует повторить процедуру и для Export. Для вычисления показателей по четвертому периоду необходимо создать дополнительные переменные, содержащие показатели изменений уровней динамического ряда за последний год. Далее нажимаем кнопку Summary: Ordinal descriptive statistics. Это приводит к вычислению разнообразных статистик, включая нужные нам: геометрическую среднею (для расчета среднего коэффициента роста) и среднею арифметическую (для расчета среднего уровня за период и среднего абсолютного прироста). Появляется расчетная таблица, для того чтобы привести ее к удобному для анализа виду необходимо транспонировать матрицу. Для этого выбираем меню Data/Transpose/File.
Рис.28 Результат расчета параметров для импорта
Рис.29 Результат расчета параметров для экспорта
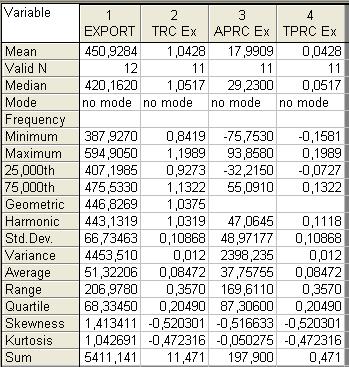
В данной таблице Mean – средняя арифметическая, этот показатель используется для нахождения среднего уровня ряда и определения среднего абсолютного прироста(APRC). Для определения среднего темпа роста используется показатель геометрической средней - Geometric (столбец TRC). Для нахождения среднего темпа прироста из последнего показателя вычитаем единицу. Результаты рассчитанных выше показателей, а также результаты показателей рассчитанных в предыдущих пунктах приведены в таблицах ниже. Для третьего периода рассчитаем отдельно все показатели и построим гравики.
Посчитаем основные параметры для третьего периода.
Рис. 30. Исходные данные за третий период с рассчитанными для низ показателями
Рис. 31. Результат расчета параметров для импорта
Рис. 32. Результат расчета параметров для экспорта
Таблица 2. Расчет показателей Import
Таблица 3. Расчет показателей Export
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1783; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.015 с.) |

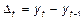 ,
, ,
,
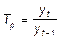 ¾ цепные темпы роста;
¾ цепные темпы роста; ¾ базисные темпы роста,
¾ базисные темпы роста, ¾ темп роста за весь период.
¾ темп роста за весь период. ,
, ,
, есть темп роста за этот период. Тогда Тпр = Тр - 1, еслитемп роста и темп прироста выражаются в виде коэффициентов, и Тпр (%)= Тр (%) - 100, если они выражаются в процентах.
есть темп роста за этот период. Тогда Тпр = Тр - 1, еслитемп роста и темп прироста выражаются в виде коэффициентов, и Тпр (%)= Тр (%) - 100, если они выражаются в процентах.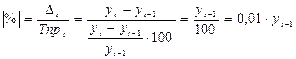
















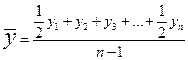
 ,
, , может быть найден по формуле:
, может быть найден по формуле: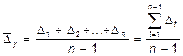 ,
,
 ,
,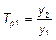 ;
;  ,..., в формуле средней геометрической подкоренное выражение преобразуется:
,..., в формуле средней геометрической подкоренное выражение преобразуется: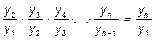
 ,
, ,
,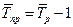 (в виде коэффициентов) и
(в виде коэффициентов) и  .
.