Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Показатели анализа ряда динамикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При изучении динамики общественных явлений возникает проблема описания интенсивности изменения и расчета средних показателей динамики. Анализ интенсивности изменения во времени осуществляется с помощью показателей, получаемых в результате сравнения уровней. К таким показателям относятся абсолютный прирост, темп роста, темп прироста, абсолютное значение одного процента прироста. Система средних показателей включает средний уровень ряда, средний абсолютный прирост, средний темп роста, средний темп прироста. Показатели анализа динамики могут вычисляться на постоянной и переменных базах сравнения. При этом принято называть сравниваемый уровень отчетным, а уровень, с которым производится сравнение, – базисным. Для расчета показателей анализа динамики на постоянной базе каждый уровень ряда сравнивается с одним и тем же базисным уровнем. В качестве базисного выбирается либо начальный уровень в ряду динамики, либо уровень, с которого начинается какой-то новый этап развития явления. Исчисляемые при этом показатели называются базисными. Для расчета показателей анализа динамики на переменной базе каждый последующий уровень ряда сравнивается с предыдущим. Вычисленные таким образом показатели анализа динамики называются цепными. Важнейшим статистическим показателем анализа динамики является абсолютный прирост (сокращение), т.е. абсолютное изменение, характеризующее увеличение или уменьшение уровня ряда за определенный промежуток времени. Абсолютный прирост с переменной базой называют скоростью роста.
Цепные и базисные абсолютные приросты представлены в табл. 7.2. Они показывают прирост (сокращение) производства электроэнергии РФ по годам и абсолютное изменение по сравнению с 1992 г. Цепные и базисные абсолютные приросты связаны между собой: сумма последовательных цепных абсолютных приростов равна базисному, т.е. общему приросту за весь промежуток времени (Σ∆y ц = ∆y б). По данным табл. 7.2 сумма последовательных цепных абсолютных приростов равна базисному приросту за весь период:
Σ∆y ц = –81 – 16 – 13 – 13 – 7 = –130.
Для оценки интенсивности, т.е. относительного изменения уровня динамического ряда за какой-либо период времени, исчисляют темпы роста (снижения).
Интенсивность изменения уровня оценивается отношением отчетного уровня к базисному. Показатель интенсивности изменения уровня ряда, выраженный в долях единицы, называется коэффициентом роста, а в процентах – темпом роста. Эти показатели интенсивности изменения отличаются только единицами измерения.
Коэффициент роста (снижения) показывает, во сколько раз сравниваемый уровень больше уровня, с которым производится сравнение (если этот коэффициент больше единицы) или какую часть уровня, с которым производится сравнение, составляет сравниваемый уровень (если он меньше единицы). Темп роста всегда представляет собой положительное число.
Цепные и базисные коэффициенты роста, характеризующие интенсивность изменения производства электроэнергии в России по годам и за весь период, исчислены в табл. 7.2. Между цепными и базисными коэффициентами роста существует взаимосвязь (если базисные коэффициенты исчислены по отношению к начальному уровню ряда динамики): произведение последовательных цепных коэффициентов роста равно базисному коэффициенту роста за весь период
Проверим взаимосвязь цепных и базисных темпов роста на нашем примере:
П = 0,915 ∙ 0,982 ∙ 0,985 ∙ 0,985 ∙ 0,992 = 0,864.
Относительную оценку скорости измерения уровня ряда в единицу времени дают показатели темпа прироста (сокращения). Темп прироста (сокращения) показывает, на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения, и вычисляется как отношение абсолютного прироста к абсолютному уровню, принятому за базу сравнения. Темп прироста может быть положительным, отрицательным или равным нулю и выражается в процентах и долях единицы (коэффициенты прироста).
Темп прироста (сокращения) можно получить и из темпа роста, выраженного в процентах, если из него вычесть 100%. Коэффициент прироста получается вычитанием единицы из коэффициента роста:
Т пр = Т р – 100, (7.5, а) Кпр = Кр – 1. (7.5, б)
Цепные и базисные темпы прироста (сокращения) производства электроэнергии исчислены в табл. 7.2. При анализе динамики развития следует также знать, какие абсолютные значения скрываются за темпами роста и прироста. Сравнение абсолютного прироста и темпа прироста за одни и те же периоды времени показывает, что при снижении (замедлении) темпов прироста абсолютный прирост не всегда уменьшается, в отдельных случаях он может возрастать. Поэтому, чтобы правильно оценить значение полученного темпа прироста, его рассматривают в сопоставлении с показателем абсолютного прироста. Результат выражают показателем, который называют абсолютным значением (содержанием) одного процента прироста и рассчитывают как отношение абсолютного прироста к темпу прироста за тот же период времени:
Абсолютное значение одного процента прироста равно сотой части предыдущего (или базисного) уровня. Оно показывает, какое абсолютное значение скрывается за относительным показателем – одним процентом прироста. Абсолютные значения одного процента прироста исчислены в табл. 7.2. Данные показывают, что абсолютное значение одного процента прироста производства электроэнергии в России в 1993-1999 гг. снижалось. В тех случаях, когда сравнение производится с отдалением периода времени, принятого за базу сравнения, рассчитывают так называемые пункты роста, которые представляют собой разность базисных темпов роста (в процентах) двух смежных периодов. В отличие от темпов прироста, которые нельзя ни суммировать, ни перемножать, пункты роста можно суммировать, в результате получаем темп прироста соответствующего периода по сравнению с базисным. По данным табл. 7.2, сумма пунктов роста равна 13,6%, что соответствует темпу прироста уровня изучаемого показателя в 1998 г. по сравнению с 1993 г. Для более глубокого понимания характера явления необходимо показатели динамики анализировать комплексно, совместно. Для обобщающей характеристики динамики исследуемого явления определяют следующие средние показатели. – Средний уровень ряда характеризует обобщенную величину абсолютных уровней. Он рассчитывается по средней хронологической, т.е. по средней исчисленной из значений, изменяющихся во времени. Методы расчета среднего уровня интервального и моментного рядов динамики различны. Для интервальных рядов динамики из абсолютных уровней средний уровень за период времени определяется по формуле средней арифметической: • при равных интервалах применяется средняя арифметическая простая:
– Сводной обобщающей характеристикой интенсивности изменения уровней ряда динамики служит средний темп роста (снижения), показывающий, во сколько раз в среднем за единицу времени изменяется уровень ряда динамики. Средний темп роста (снижения) – обобщенная характеристика индивидуальных темпов роста ряда динамики. В качестве основы и критерия правильности исчисления среднего темпа роста (снижения) применяется определяющий показатель – произведение цепных темпов роста, равное темпу роста за весь рассматриваемый период. Следовательно, если значение признака образуется как произведение отдельных вариантов, то согласно общему правилу (см. § 5.1) нужно применять среднюю геометрическую. Поскольку средний темп роста представляет собой средний коэффициент роста, выраженный в процентах
Следовательно, с 1994 по 1999 г. производство электроэнергии в России снижалось в среднем на 2,9% в год, т.е. (0,971 ∙ 100 – 100). Если известны уровни динамического ряда, то расчет среднего коэффициента роста упрощается. Так как произведение цепных коэффициентов роста равно базисному, то в подкоренное выражение подставляется базисный коэффициент роста. Базисный коэффициент, как известно, получается непосредственно как частное от деления уровня последнего периода уn на уровень базисного периода у0. Тогда формула для расчета среднего коэффициента роста для равностоящих рядов динамики (по «базисному способу»):
где т – число уровней ряда динамики в изучаемом периоде, включая базисный. Для расчета средних коэффициентов роста по формуле (7.14) не нужно знать годовые темпы. Для нашего примера:
Получен тот же результат, расчеты упрощены. – Средние темпы прироста (сокращения) рассчитываются на основе средних темпов роста вычитанием из последних ста процентов. Соответственно при исчислении средних коэффициентов прироста из значений коэффициентов роста вычитается единица:
Так, в нашем примере среднегодовой темп прироста производства электроэнергии характеризуется отрицательным значением (–2,9%), что свидетельствует о ежегодном сокращении производства электроэнергии. При анализе развития явлений, отражаемых двумя динамическими рядами, представляет интерес сравнение интенсивностей изменения во времени обоих явлений. Такое сопоставление интенсивностей изменения производится при сравнении динамических рядов одинакового содержания, но относящихся к разным территориям (странам, республикам, районам и т.п.), или к различным организациям (министерствам, предприятиям, учреждениям), или при сравнении рядов разного содержания, но характеризующих один и тот же объект. Например, сравнение рядов динамики, характеризующих производство важнейших видов продукции в Российской Федерации и других странах. Сравнительные характеристики направления и интенсивности роста одновременно развивающихся во времени явлений определяются приведением рядов динамики к общему (единому) основанию и расчетом коэффициентов опережения (отставания). – Ряды динамики (в которых возникают, например, проблемы сопоставимости цен сравниваемых стран, методики расчета сравниваемых показателей и т.п.) обычно приводят к одному основанию, если они не могут быть решены другими методами. По исходным уровням нескольких рядов динамики определяют относительные величины – базисные темпы роста или прироста. Принятый при этом за базу сравнения период времени (дата) выступает в качестве постоянной базы расчетов темпов роста для каждого из изучаемых рядов динамики. В зависимости от целей исследования базой может быть начальный, средний или другой уровень ряда.
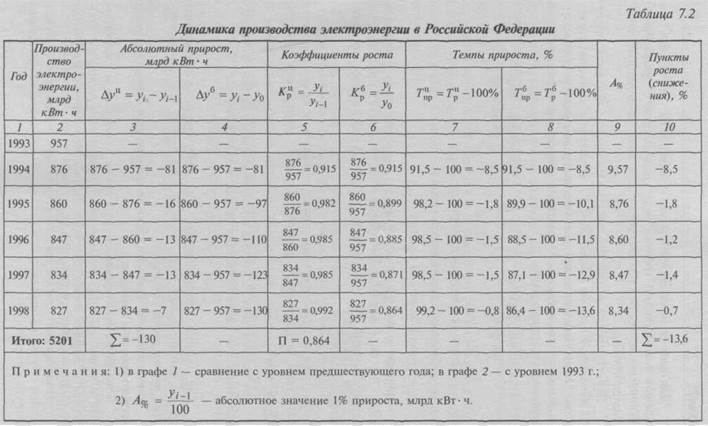
По данным табл. 7.3 (числитель) можно проследить снижение объемов производства продукции машиностроения и металлообработки как в России, так и в Беларуси. Однако непосредственно по ним нельзя определить, в какой стране это снижение идет быстрее, так как различны значения абсолютных уровней этих рядов.
Приведем абсолютные уровни рядов к одному основанию, приняв за базу сравнения уровни 1990 г., и получим сравнимые показатели – базисные темпы изменения (см. табл. 7.3, знаменатель), которые показывают, что темпы снижения объемов производства продукции машиностроения и металлообработки в России заметно превосходят соответствующие показатели Беларуси. – Сравнение интенсивности изменений уровней рядов во времени возможно с помощью коэффициентов опережения (отставания), представляющих собой отношение базисных темпов роста (или прироста) двух рядов динамики за одинаковые отрезки времени:
Коэффициенты опережения (отставания) могут быть исчислены на основе сравнения средних темпов роста (или прироста) двух динамических рядов за одинаковый период времени:
Коэффициент опережения (отставания) показывает, во сколько раз быстрее растет (отстает) уровень одного ряда динамики по сравнению с другим. При этом сравнении темпы должны характеризовать тенденцию одного направления. Для нашего примера в 1995 г.
Это значит, что производство продукции машиностроения и металлообработки в России в 1990-1995 гг. сокращалось в 1,6 раза быстрее, чем в Беларуси. Показатели динамических рядов имеют большое практическое значение и находят самое широкое применение в анализе общественных явлений и процессов. Для закрепления изложенного материала рассмотрим решение еще четырех задач на исчисление показателей анализа ряда динамики (данные условные). Задача 1. Динамика выпускаемой предприятием продукции (в сопоставимых ценах) характеризуется следующими данными, млрд руб.:
Задача 2. Остатки вкладов в районных филиалах Сбербанка РФ за первый квартал характеризуются следующими данными, представленными в табл. 7.4. Таблица 7.4
|
||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 770; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.117.164 (0.014 с.) |



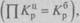 а частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста. Взаимосвязь легко проверить:
а частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста. Взаимосвязь легко проверить:





 то для равностоящих рядов динамики расчеты по средней геометрической сводятся к исчислению средних коэффициентов роста из цепных коэффициентов роста (по «цепному способу»):
то для равностоящих рядов динамики расчеты по средней геометрической сводятся к исчислению средних коэффициентов роста из цепных коэффициентов роста (по «цепному способу»):