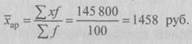Распределение рабочих АО по уровню оплаты труда

 

Исходные данные	Расчетные значения
Группы рабочих по оплате труда, руб.	Число рабочих f, чел.	Середина интервала х, руб.	x ∙ f
До 1000			4 500
1000-1200			16 500
1200-1400			26 000
1400-1600			45 000
1600-1800			27 200
1800 и более			26 600
Итого		–	145 800

 

От интервального ряда перейдем к дискретному путем замены интервальных значений их средними значениями (простая средняя между верхней и нижней границами каждого интервала). При этом величины открытых интервалов (первый и последний) условно приравниваются к интервалам, примыкающим к ним (второй и предпоследний).

При таком исчислении средней допускается некоторая неточность, поскольку делается предположение о равномерности распределения единиц признака внутри группы. Однако ошибка будет тем меньше, чем уже интервал и чем больше единиц в интервале.

После того как найдены середины интервалов, вычисления делают так же, как и в дискретном ряду, – варианты умножают на частоты (веса) и сумму произведений делят на сумму частот (весов):

 

 

Итак, средний уровень оплаты труда рабочих АО составляет 1458 руб. в месяц.

Вычисление средней арифметической часто сопряжено с большими затратами времени и труда. Однако в ряде случаев процедуру расчета средней можно упростить и облегчить, если воспользоваться ее свойствами. Приведем (без доказательства) некоторые основные свойства средней арифметической.

Свойство 1. Если все индивидуальные значения признака (т.е. все варианты) уменьшить или увеличить в i раз, то среднее значение нового признака соответственно уменьшится или увеличится в i раз.

Свойство 2. Если все варианты осредняемого признака уменьшить или увеличить на число А, то средняя арифметическая соответственно уменьшится или увеличится на это же число А.

Свойство 3. Если веса всех осредняемых вариантов уменьшить или увеличить в к раз, то средняя арифметическая не изменится.

В качестве весов средней вместо абсолютных показателей можно использовать удельные веса в общем итоге (доли или проценты). Тем самым достигается упрощение расчетов средней.

Для упрощения расчетов средней идут по пути уменьшения значений вариантов и частот. Наибольшее упрощение достигается, когда в качестве А выбирается значение одного из центральных вариантов, обладающего наибольшей частотой, в качестве i – величина интервала (для рядов с одинаковыми интервалами). Величина А называется началом отсчета, поэтому такой метод вычисления средней называется «способом отсчета от условного нуля» или «способом моментов».

Допустим, что все варианты х сначала уменьшены на одно и то же число А, а затем уменьшены в i раз. Получим новый вариационный ряд распределения новых вариантов (х₁).

 

 

Итак, средняя стоимость основных производственных фондов предприятий региона составляет 19 млн руб.

Применение способа моментов настолько облегчает расчеты, что позволяет их выполнять без использования вычислительной техники даже при больших и многозначных числах, характеризующих индивидуальные значения осредняемых показателей.

Средняя гармоническая

 

При расчете средних показателей помимо средней арифметической могут использоваться и другие виды средних. Однако любая средняя величина должна вычисляться так, чтобы при замене ею каждого варианта осредняемого признака не изменялся итоговый, обобщающий, или, как его принято называть, определяющий показатель, который связан с осредняемым показателем (например, при замене фактических скоростей на отдельных отрезках пути их средней скоростью не должно измениться общее расстояние, пройденное транспортным средством за одно и то же время; при замене фактических заработных плат отдельных работников предприятия средней заработной платой не должен измениться фонд заработной платы). Следовательно, в каждом конкретном случае в зависимости от характера имеющихся данных существует только одно истинное среднее значение показателя, адекватное свойствам и сущности изучаемого социально-экономического явления.

Вид средней определяется характером взаимосвязи определяющего показателя с осредняемым.

Средняя арифметическая, как было показано выше, применяется в тех случаях, когда известны варианты варьирующего признака х и их частоты f.

Когда статистическая информация не содержит частот f по отдельным вариантам х совокупности, а представлена как их произведение x ∙ f, применяется формула средней гармонической взвешенной. Чтобы исчислить среднюю, обозначим x ∙ f = w, откуда f = w / x. Теперь преобразуем формулу средней арифметической таким образом, чтобы по имеющимся данным х и w можно было исчислить среднюю. В формулу средней арифметической взвешенной (5.4) вместо xf подставим w, вместо f – отношение w / x и получим формулу средней гармонической взвешенной:

 

 

Из формулы (5.9) видно, что средняя гармоническая – средняя взвешенная из варьирующих обратных значений признака. Она является преобразованной формой арифметической средней и тождественна ей. Вместо гармонической всегда можно рассчитать среднюю арифметическую, но для этого сначала нужно определить веса отдельных значений признака, скрытые в весах средней гармонической.

Таким образом, средняя гармоническая применяется тогда, когда неизвестны действительные веса f, а известно w = x ∙ f, т.е. в тех случаях, когда средняя предназначается для расчета сумм слагаемых, обратно пропорциональных величине данного признака, когда суммированию подлежат не сами варианты, а обратные им величины.

Например, по данным табл. 5.5 требуется определить среднюю цену 1 кг яблок в апреле.

Таблица 5.5