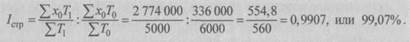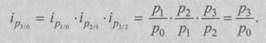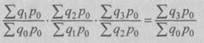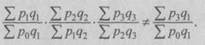Среднемесячная заработная плата и число работников

 

№ п/п	Отрасль экономики	Заработная плата, руб.	Число работников, чел.
Январь	Сентябрь	Январь	Сентябрь
x0	x1	Т0	Т1
	Здравоохранение
	Образование
	Культура и искусство

 

Исчислить: индекс заработной платы переменного состава, постоянного состава и структурных сдвигов.

Решение.

1. Для исчисления индекса заработной платы переменного состава вначале определим среднюю заработную плату в январе и сентябре. Обозначим заработную плату – х, а число работников – T.

Январь:

 

 

Следовательно, средняя заработная плата работников по перечисленным отраслям экономики выросла в сентябре по сравнению с январем на 13,8%.

Абсолютный прирост средней заработной платы составил:

 

637,2 – 560 = 77,2 руб.

 

Изменение средней заработной платы происходило под влиянием изменений уровня заработной платы в каждой отрасли экономики и структуры численности работников.

 

 

Следовательно, средняя заработная плата работников по указанным отраслям экономики выросла в сентябре по сравнению с январем на 14,9% в результате изменения только одного фактора – самой заработной платы по каждой отрасли экономики (без учета структурных изменений в численности работников).

Абсолютный прирост средней заработной платы составил:

 

637,2 – 554,8 = 82,4 руб.

 

4. Вычислим влияние изменения структуры численности работников на динамику средней заработной платы на основе индекса структурных сдвигов:

 

 

Следовательно, увеличение доли работников с меньшей заработной платой в общей их численности привело к снижению средней заработной платы по трем отраслям вместе на 0,03%, хотя в каждой отрасли по отдельности она возросла.

Абсолютное снижение средней заработной платы составило: 554,8 – 560 = –5,2 руб., что совпадает с разностью исчисленных выше приростов заработной платы: 77,2 – 82,4 = –5,2 руб.

Отрицательный эффект структурных сдвигов объясняется тем, что в сентябре по сравнению с январем в большей мере сократилась доля работников с наиболее высоким уровнем заработной платы, т.е. в здравоохранении (с 40 до 32%).

Базисные и цепные индексы

 

Часто в ходе экономического анализа изменение индексируемых величин изучают не за два, а за ряд последовательных периодов. Следовательно, возникает необходимость построения индексов за ряд этих последовательных периодов, которые образуют индексные системы. Такие системы характеризуют изменения, происходящие в изучаемом явлении в течение исследуемого периода времени.

В зависимости от базы сравнения индексы бывают базисными и цепными.

В системе базисных индексов сравнения уровней индексируемого показателя в каждом индексе производится с уровнем базисного периода, а в системе цепных индексов уровни индексируемого показателя сопоставляются с уровнем предыдущего периода.

Цепные и базисные индексы могут быть как индивидуальные, так и общие.

Ряды индивидуальных индексов просты по построению. Так, например, обозначив четыре последовательных периода подстрочными значениями 0, 1, 2, 3, исчисляем базисные и цепные индивидуальные индексы цен:

 

 

Между цепными и базисными индивидуальными индексами существует взаимосвязь, позволяющая переходить от одних индексов к другим – произведение последовательных цепных индивидуальных индексов дает базисный индекс последнего периода:

 

 

Отношение базисного индекса отчетного периода к базисному индексу предшествующего периода дает цепной индекс отчетного периода:

 

 

Это правило позволяет применять так называемый цепной метод, т.е. находить неизвестный ряд базисных индексов по известным цепным, и наоборот.

Рассмотрим возможность применения цепного метода исчисления для агрегатных индексов.

Как известно, в каждом отдельном индексе веса в его числителе и знаменателе обязательно фиксируются на одном и том же уровне.

 

 

Период весов во всех индексах цен Пааше взят текущий (индексы с переменными весами), в индексах физического объема и индексах цен Ласпейреса – закрепленный (индексы с постоянными весами).

Постоянные веса (не меняющиеся при переходе от одного индекса к другому) позволяют исключить влияние изменения структуры на значение индекса.

Ряды агрегатных индексов с постоянными весами имеют преимущество – сохраняется взаимосвязь между цепными и базисными индексами, например, в ряду агрегатных индексов физического объема:

 

 

или в ряду агрегатных индексов цен Ласпейреса:

 

 

Таким образом, использование постоянных весов в течение ряда лет позволяет переходить от цепных общих индексов к базисным, и наоборот.

В рядах агрегатных индексов качественных показателей, которые строятся с переменными весами (например, ряд цен Пааше), перемножение цепных индексов не дает базисный:

 

 

Для таких индексов переход от цепных индексов к базисным (и наоборот) невозможен. Вместе с тем в статистической практике часто возникает необходимость определения динамики цен за длительный период времени на основе цепных индексов цен с переменными весами. Тогда для получения приближенного базисного (итогового) индекса цепные индексы цен перемножают, заведомо зная, что в таком расчете допускается ошибка. Отдельные индексы этого ряда используются для пересчета стоимостных показателей отчетного периода в ценах предыдущего года. Основные формулы для расчета общих индексов приведены в табл. 8.6.