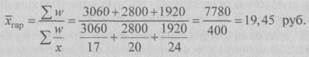Цена и выручка от реализации по трем коммерческим магазинам

 

Номер магазина	Исходные данные	Расчетные значения
Цена яблок х, руб./кг	Выручка от реализации w, руб.	Частота (количество реализованных единиц) f = w / x, кг
1-й			3070: 17 = 180
2-й			2800: 20 = 140
3-й			1920: 24 = 80
Итого	–

 

Расчет средней цены выражается соотношением:

 

 

Определяющим показателем здесь является числитель этой логической формулы. Выручка от реализации w известна (числитель), а количество реализованных единиц неизвестно, но может быть найдено как частное от деления одного показателя на другой, для чего нужно отдельно по каждому магазину разделить выручку на цену.

Тогда средняя цена 1 кг яблок по трем коммерческим магазинам может быть исчислена по формуле (5.9) средней гармонической взвешенной:

 

 

Этот же результат получится и по средней арифметической взвешенной, если в качестве весов принять количество проданных единиц (которые необходимо предварительно рассчитать):

 

 

Полученная средняя цена 1 кг яблок является реальной величиной, ее произведение на все количество проданных яблок дает общий объем реализации, выступающий в качестве определяющего показателя (7780 руб).

Исчисление средней гармонической взвешенной по формуле (5.9) освобождает от необходимости предварительного расчета весов, поскольку эта операция заложена в саму формулу.

В тех случаях, когда вес каждого варианта равен единице (индивидуальные значения обратного признака встречаются по одному разу), применяется средняя гармоническая простая, исчисляемая по формуле:

 

 

Пример. У предпринимателя имеются два автомобиля различных моделей, работающих на бензине одинаковой марки. Расход бензина у первого автомобиля равен 0,05 л/км, у второго – 0,08 л/км. Каков средний расход бензина на 100 км (или 1 км) пройденного пути?

Может показаться, что решение этой задачи заключается в расчете средней арифметической простой, т.е. расход равен

 

(0,05 + 0,008): 2 = 0,065 л/км.

 

Однако такой расчет является ошибочным. Покажем это на примере одного и того же количества израсходованного бензина.

Предположим, расход бензина на поездку составил 40 л (как будет показано ниже, конкретная цифра значения не имеет). На 40 л бензина первая машина пройдет 800 км, т.е. 40: 0,05, пробег второй – составит 500 км, т.е. 40: 0,08, следовательно, общий пробег равен 1300 км.

Если средняя исчислена правильно, то при замене индивидуальных значений их средним не должен измениться определяющий показатель – в данном случае общий пробег.

 

 

Для закрепления знаний по теме рассмотрим задачу на применение в расчетах средней арифметической и средней гармонической.

Пусть требуется определить средний размер двух видов вклада в банке в октябре и ноябре по данным табл. 5.6.

Таблица 5.6

Информация о вкладах в банке для расчета средних значений

 

Вид вклада	Октябрь	Ноябрь
Число вкладов f, тыс.	Средний размер вклада х, руб.	Сумма вкладов w, млн руб.	Средний размер вклада х, руб.
До востребования			4,07
Срочный			3,87

 

В октябре известен средний размер вкладов каждого вида х и количество вкладов f. Следовательно, для расчета среднего размера вклада по двум видам применяем формулу средней арифметической взвешенной:

 

 

В ноябре известен средний размер вкладов каждого вида, а количество вкладов неизвестно, но зато имеются данные об общих суммах этих вкладов.

Путем деления сумм вкладов w каждого вида на их средний размер вклада х можно определить веса – число вкладов f по их видам, а затем определить средний размер вклада по двум видам по формуле средней арифметической взвешенной. Однако если в расчете использовать среднюю гармоническую взвешенную, то отпадает необходимость предварительных расчетов весов – размеров вкладов по каждому виду, поскольку эта операция заложена в саму формулу.

Итак, средний размер вклада в ноябре по двум их видам находим по формуле средней гармонической взвешенной:

 

 

Средняя геометрическая

 

Средняя геометрическая применяется в тех случаях, когда индивидуальные значения признака представляют собой, как правило, относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики, т.е. характеризует средний коэффициент роста.

Средняя геометрическая исчисляется извлечением корня степени n из произведений отдельных значений – вариантов признака х:

 

 

где n – число вариантов; П – знак произведения.

Наиболее широкое применение средняя геометрическая получила для определения средних темпов изменения в рядах динамики, а также в рядах распределения.

Использование средней геометрической показано в гл. 7.