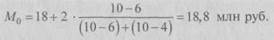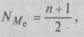I. Кузнецова, елена ивановна.

СТАТИСТИКА

 

Второе издание, переработанное и дополненное

Допущено Министерством образования Российской Федерации в качестве учебного пособия для студентов высших учебных заведений, обучающихся по экономическим специальностям

Рекомендовано учебно-методическим центром «Профессиональный учебник» в качестве учебного пособия для студентов высших учебных заведений, обучающихся по направлению «Экономика»

 

 

УДК [311:33](075.8)

ББК 65.051я73-1

Г96

 

Рецензент:

д-р экон. наук, проф. A.M. Илышев (Уральский государственный технический университет – УПИ)

 

Главный редактор издательства Н.Д. Эриашвили, кандидат юридических наук, доктор экономических наук, профессор, лауреат премии Правительства РФ в области науки и техники

Гусаров, Виктор Максимович.

Статистика: учеб. пособие для студентов вузов, обучающихся по экономическим специальностям/В.М. Гусаров, Е.И. Кузнецова. – 2-е изд., перераб. и доп. – М.: ЮНИТИ-ДАНА, 2008. – 479 с.

I. Кузнецова, Елена Ивановна.

ISBN 978-5-238-01226-1

 

Агентство CIP РГБ

 

Последовательно рассмотрены общие вопросы теории статистики (сущность и задачи статистики на современном этапе, вопросы статистической методологии); макроэкономической статистики (статистики населения и рынка труда, национального богатства, ВВП и других макроэкономических показателей, уровня жизни населения и социальной сферы, системы национальных счетов); статистики предприятия (факторов и результатов деятельности в сфере производства); статистики финансов (цен, кредита, денежного обращения, страхового рынка, рынка ценных бумаг, финансов предприятий, финансовых расчетов).

Представлены типовые примеры с решениями и контрольные вопросы по изучаемому материалу.

Для студентов и преподавателей экономических специальностей, а также для специалистов статистических, финансово-банковских, экономических органов, страховых компаний и коммерческих структур.

 

© ИЗДАТЕЛЬСТВО ЮНИТИ-ДАНА, 2001, 2007

Принадлежит исключительное право на использование и распространение издания. Воспроизведение всей книги или любой ее части любыми средствами или в какой-либо форме, в том числе в Интернет-сети, запрещается без письменного разрешения издательства.

© Оформление «ЮНИТИ-ДАНА», 2007

Оглавление

Предисловие

Раздел I. Теория статистики

Глава 1. Статистика как наука

1.1. Понятие статистики и краткие сведения из ее истории

1.2. Предмет статистики

1.3. Метод статистики

1.4. Основные категории статистики

1.5. Задачи статистики и основные направления ее реформирования

Контрольные вопросы

Глава 2. Источники статистической информации

2.1. Статистическая информация и ее распространение

2.2. Статистическое наблюдение

2.2.1. Понятие о статистическом наблюдении

2.2.2. Программно-методологические вопросы статистического наблюдения

2.2.3. Формы, виды и способы наблюдения

Контрольные вопросы

Глава 3. Сводка и группировка материалов статистического наблюдения

3.1. Сводка и группировка статистических данных

3.2. Задачи и виды группировок

3.3. Выполнение группировки по количественному признаку

3.4. Статистические ряды распределения

Контрольные вопросы

Глава 4. Абсолютные и относительные статистические величины

4.1. Абсолютные статистические величины

4.2. Относительные статистические величины

Контрольные вопросы

Глава 5. Средние величины и показатели вариации

5.1. Понятие о средних величинах

5.2. Виды средних и способы их вычисления

5.2.1. Средняя арифметическая

5.2.2. Расчет средней арифметической в рядах распределения

5.2.3. Средняя гармоническая

5.2.4. Средняя геометрическая

5.2.5. Средняя квадратическая и средняя кубическая

5.2.6 Структурные средние

5.3. Показатели вариации

5.3.1. Правило сложения дисперсий

Контрольные вопросы

Глава 6. Выборочный метод в статистике

6.1. Понятие о выборочном наблюдении, его задачи

6.2. Ошибки выборки

6.3. Распространение выборочных результатов на генеральную совокупность

Контрольные вопросы

Глава 7. Статистическое изучение динамики

7.1. Понятие о рядах динамики

7.2. Правила построения рядов динамики

7.3. Показатели анализа ряда динамики

7.4. Методы анализа основной тенденции развития в рядах динамики

7.5. Методы изучения сезонных колебаний

7.6. Экстраполяция в рядах динамики и прогнозирование

Контрольные вопросы

Глава 8. Экономические индексы

8.1. Индексы и их классификация

8.2. Общие индексы количественных показателей

8.3. Общие индексы качественных показателей

8.4. Индексы средних величин

8.5. Базисные и цепные индексы

8.6. Система взаимосвязанных индексов. Факторный анализ

Контрольные вопросы

Раздел II. Макроэкономическая статистика

Глава 10.Статистика населения и трудовых ресурсов

10.1. Показатели численности населения, методы их расчета

10.2. Статистика естественного движения и миграции населения

10.2.1. Изучение естественного движения населения

10.2.2. Изучение миграции населения

10.2.3. Расчет перспективной численности населения

10.3. Статистика занятости и безработицы

Контрольные вопросы

Глава 11. Статистика национального богатства

11.1. Показатели объема, структуры и динамики национального богатства

11.1.1. Нефинансовые активы

11.1.2. Финансовые активы

11.2. Система показателей статистики национального богатства

Контрольные вопросы

Раздел III. Статистика предприятия

Глава 19. Статистика оборотных фондов

19.1. Показатели наличия и использования оборотных фондов

19.2. Определение потребности в оборотных фондах

Контрольные вопросы

Глава 21. Статистика цен

21.1. Сущность цены и ее виды

21.2. Статистическое изучение цен

21.3. Индексы потребительских цен и покупательной способности рубля

21.4. Статистика инфляции

Контрольные вопросы

Библиографический список

Предисловие

 

Эффективное социально-экономическое развитие страны, государственное управление и регулирование связаны с необходимостью своевременного получения и анализа полной, достоверной, научно обоснованной официальной статистической информации о социальных, экономических, демографических, экологических и других общественных явлениях.

Важную роль в механизме управления экономикой выполняет статистика, осуществляя сбор, научную обработку, обобщение и анализ информации, характеризующей развитие экономики страны, культуры и уровня жизни населения. В результате предоставляется возможность выявления взаимосвязей в экономике, изучения динамики ее развития, проведения международных сопоставлений и принятия эффективных управленческих решений на государственном и региональных уровнях. Поэтому в системе экономического образования особое место отводится изучению статистики – базовой научной дисциплины, формирующей профессиональный уровень современного экономиста.

В настоящее время перед наукой встает принципиально новая задача – реформирование общеметодологических и организационных основ статистики, а также приведение ее в соответствие с международными правилами. Успешное выполнение этой задачи требует дальнейшего повышения качества подготовки экономистов высшей квалификации.

В учебном пособии рассмотрены основные методы статистического исследования (статистическое наблюдение, сводка, группировка, расчет обобщающих показателей, выборочный метод, анализ рядов динамики, индексный метод анализа, основы корреляционного и регрессионного анализа). Показана необходимость их комплексного применения в анализе элементов рыночной экономики. Особое внимание уделено обоснованию вероятностного характера статистического вывода. Теория статистической методологии подкреплена иллюстрацией применения статистических методов в исследованиях конкретных социально-экономических процессов.

На современном этапе государственная статистика развивается в условиях осуществления в России значительных социально-экономических перемен, административной реформы, реформирования бюджетного процесса, перехода на международные стандарты финансовой отчетности, что определяет задачи поиска и реализации принципиально новых подходов к официальной статистической деятельности, формированию гибкой, быстро реагирующей на изменение жизни общества системы информационно-статистического обеспечения.

Кроме того, необходимость дальнейшего развития государственной статистики вызвана:

• нерешенностью ряда методологических проблем статистики, возникающих при вхождении России в мировое сообщество и выполнении ее обязательств перед международными организациями, в том числе статистическими;

• отсутствием показателей, отражающих новые социально-экономические явления и процессы и необходимых для анализа развития российской экономики и российского общества;

• «распыленностью» информации и трудностями, возникающими у пользователей при получении необходимой информации;

• несовершенством законодательной базы для получения статистической информации и обеспечения ею всех заинтересованных пользователей;

• отсутствием регламентации прав и обязанностей федеральных органов исполнительной власти при формировании статистических информационных ресурсов и получении информации из них.

Необходимо разработать новые, не используемые в статистической практике показатели и алгоритмы их расчета, определить источники и методы получения первичных данных, создать программно-технологическое обеспечение, а также определить процедуры согласования и представления итоговых данных.

Указанные задачи и накопленный потенциал государственной статистики требуют продолжения преобразований, в связи с чем в данном учебном пособии нашло отражение расширение задач отечественной статистики в связи с выполнением Федеральной целевой программы «Развитие государственной статистики России в 2007-2011 годах».

В учебном пособии четыре раздела.

В разделе I «Теория статистики» освещен предмет статистики, определены ее задачи, рассмотрены вопросы статистической методологии, показано применение важнейших методов статистического исследования социально-экономических явлений.

В разделе II «Макроэкономическая статистика» рассмотрены система показателей и методика их расчета, в совокупности обеспечивающих количественную характеристику результатов функционирования экономики страны и регионов в разрезе отраслей, секторов и форм собственности; уровень жизни населения; система национальных счетов как макростатис-тическая модель экономики.

Раздел III «Статистика предприятия» посвящен анализу функционирования предприятия, условий применения и потребления основного и оборотного капитала и рабочей силы, характеристике натурально-вещественных и финансовых результатов производства.

Раздел IV «Статистика финансов» посвящен количественному и качественному анализу финансово-денежных отношений, возникающих в процессе производства. Рассмотрены вопросы статистики цен, кредита, денежного обращения, страхового рынка, рынка ценных бумаг, финансов предприятий, финансовых расчетов.

Второе издание учебного пособия «Статистика» после смерти его автора В.М. Гусарова дополнено и переработано канд. экон. наук Е.И. Кузнецовой.

Раздел I. Теория статистики

 

Предмет статистики

 

Статистика, как любая наука, требует определения предмета исследования. В связи с этим различают статистику, занимающуюся изучением социально-экономических явлений, которая относится к циклу общественных наук, и статистику, занимающуюся закономерностями явлений природы, которая относится к естественным наукам.

Настоящий курс посвящен статистике социально-экономических явлений.

Объектом изучения социально-экономической статистики (или просто статистики) является общество во всем многообразии его форм и проявлений. Но общество и протекающие в нем процессы и закономерности развития изучают и другие общественные науки – экономическая теория (политическая экономия), экономика промышленности, сельского хозяйства, социология и др. При этом каждая из этих наук находит в этом объекте свой специфический аспект изучения – предмет познания.

Имеет свой предмет познания и статистика. Говоря о специфике предмета статистики, ее связывают обычно с анализом взаимоотношений количественного и качественного аспектов выражения социально-экономических процессов. Оба эти аспекта неразрывно связаны между собой. В каждый исторический момент социальные и экономические явления имеют определенные размеры, уровни, между ними существуют определенные количественные соотношения. Таковы, например, численность населения страны на определенную дату, темпы роста валового внутреннего продукта, изменения уровня заработной платы, цен на потребительские товары и др.

Количественные изменения общественных явлений и процессов в неразрывной связи с их качественным содержанием и изучает статистика как наука.

Таким образом, предметом статистики выступают размеры и количественные соотношения качественно определенных социально-экономических явлений, закономерности их связи и развития в конкретных условиях места и времени.

Свой предмет статистика изучает методом обобщающих показателей.

В определении предмета статистики подчеркивается несколько характерных особенностей статистики как науки. Статистика изучает:

• массовые общественные явления при помощи статистических показателей (численность населения, количество произведенной в стране конкретной промышленной, сельскохозяйственной, строительной и другой продукции за определенный период времени) и их динамику (изменение уровня жизни населения и т.д.);

• количественную сторону массовых общественных явлений и дает количественное, цифровое освещение общественных явлений;

• количественную сторону общественных явлений в неразрывной связи с их качественным содержанием; наблюдает в обществе процесс перехода количественных изменений в качественные (так, количественные изменения структуры экспорта и импорта товаров свидетельствуют о качественных изменениях в экономике страны);

• количественную сторону общественных явлений в конкретных условиях места и времени (динамику численности населения, занятости его по секторам экономики, объема производства, распределения доходов, потребления и т.д.); характеризует явления общественной жизни в конкретных пространственных и временных границах;

• количественные связи между общественными явлениями с помощью специальной методологии; использует математические методы при исчислении ряда статистических показателей (ошибок выборки, тесноты связи и т.д.), в свою очередь, гуманитарные и естественные науки широко используют в своих исследованиях статистические методы сбора, обработки и анализа данных.

Теоретической основой статистики являются положения социально-экономической теории, которые рассматривают законы развития социально-экономических явлений, выясняют их природу и значение в жизни общества. Опираясь на знания положений экономической теории, статистика анализирует конкретные формы проявления категорий, оценивает размеры явлений, осуществляет разработку адекватных методов их изучения и анализа. В условиях процесса познания связь между экономической теорией и статистикой носит ступенчатый характер: экономическая теория – статистика – экономическая теория и т.д.

Итак, статистика – комплекс учебных дисциплин, обеспечивающих овладение методологией статистического исследования массовых социально-экономических явлений и процессов с целью выявления закономерностей их развития в конкретных условиях места и времени.

Метод статистики

 

Для изучения предмета статистики разработаны и применяются специфические приемы, совокупность которых образует методологию статистики (методы массовых наблюдений, группировок, обобщающих показателей, динамических рядов, индексный метод и др.). Применение в статистике конкретных методов предопределяется поставленными задачами и зависит от характера исходной информации.

Общей основой разработки и применения статистической методологии является диалектический метод познания, согласно которому общественные явления и процессы рассматриваются в развитии, взаимной связи и причинной обусловленности. Знание законов общественного развития создает фундамент, с помощью которого можно понять и правильно истолковать явления, подлежащие статистическому исследованию, выбрать надлежащую методику его изучения и анализа.

При этом статистика опирается на такие диалектические категории, как количество и качество, необходимость и случайность, причинность и закономерность, единичное и массовое, индивидуальное и общее.

Статистические методы используются комплексно (системно). Это обусловлено сложностью процесса экономико-статистического исследования, состоящего из трех основных стадий:

первая – сбор первичной статистической информации;

вторая – статистическая сводка и обработка первичной информации;

третья – обобщение и интерпретация статистической информации.

На первой стадии статистического исследования, в связи с необходимостью учета всего многообразия фактов и форм осуществления социально-экономических процессов и в соответствии с их массовым характером, применяется метод массового статистического наблюдения, обеспечивающий всеобщность, полноту и представительность (репрезентативность) полученной первичной информации.

На второй стадии собранная в ходе массового наблюдения информация подвергается обработке методом статистических группировок, позволяющим выделить в изучаемой совокупности социально-экономические типы; совершается переход от характеристики единичных фактов к характеристике данных, объединенных в группы величин. Методы группировки различаются в зависимости от задач исследования и качественного состояния первичного материала.

На третьей стадии проводится анализ статистической информации на основе применения обобщающих статистических показателей: абсолютных, относительных и средних величин, вариации, тесноты связи и скорости изменения социально-экономических явлений во времени, индексов и др. Проведение анализа позволяет проверить причинно-следственные связи изучаемых явлений и процессов, определить влияние и взаимодействия различных факторов, оценить эффективность принимаемых управленческих решений, возможные экономические и социальные последствия складывающихся ситуаций.

При изучении статистической информации широкое применение имеют табличный и графический методы.

Статистическая методология получила развитие в работах видных отечественных ученых-статистиков: B.C. Немчинова, С.Г. Струмилина, В.Н. Старовского, В.И. Хотимского, Б.С. Ястремского, А.Я. Боярского, Т.В. Рябушкина, Н.К. Дружинина и др.

Статистическое наблюдение

Понятие о средних величинах

 

Как правило, многие признаки единиц статистических совокупностей различны по своему значению, например, заработная плата рабочих одной профессии какого-либо предприятия не одинакова за один и тот же период времени, различны урожайность сельскохозяйственных культур в хозяйствах района и цены на рынке на одинаковую продукцию и т.д. Поэтому, чтобы определить значение признака, характерное для всей изучаемой совокупности единиц, прибегают к расчету средних величин.

Средней величиной в статистике называется обобщающий показатель, характеризующий типичный уровень явления в конкретных условиях места и времени, отражающий величину варьирующего признака в расчете на единицу качественно однородной совокупности.

В экономической практике используется широкий круг показателей, вычисленных в виде средних величин. Например, обобщающим показателем доходов рабочих акционерного общества (АО) служит средний доход одного рабочего, определяемый отношением фонда заработной платы и выплат социального характера за рассматриваемый период (год, квартал, месяц) к численности рабочих АО. Для лиц с достаточно однородным уровнем доходов, например работников бюджетной сферы и пенсионеров по старости (исключая имеющих льготы и дополнительные доходы), можно определить типичные доли расходов на покупку предметов питания. Так, можно говорить о средней продолжительности рабочего дня, среднем тарифном разряде рабочих, среднем уровне производительности труда и т.д.

Вычисление среднего – один из распространенных приемов обобщения; средний показатель отражает то общее, что характерно (типично) для всех единиц изучаемой совокупности, в то же время он игнорирует различия отдельных единиц. В каждом явлении и его развитии имеет место сочетание случайности и необходимости. При исчислении средних в силу действия закона больших чисел случайности взаимопогашаются, уравновешиваются, поэтому можно абстрагироваться от несущественных особенностей явления, от количественных значений признака в каждом конкретном случае. В способности абстрагироваться от случайности отдельных значений, колебаний и заключена научная ценность средних как обобщающих характеристик совокупностей.

Там, где возникает потребность обобщения, расчет таких характеристик приводит к замене множества различных индивидуальных значений признака средним показателем, характеризующим всю совокупность явлений, что позволяет выявить закономерности, присущие массовым общественным явлениям, незаметные в единичных явлениях.

Средняя отражает характерный, типичный, реальный уровень изучаемых явлений, характеризует эти уровни и их изменения во времени и в пространстве.

Средняя – это сводная характеристика закономерностей процесса в тех условиях, в которых он протекает.

Анализ средних выявляет, например, закономерности изменения производительности труда, заработной платы рабочих отдельного предприятия на определенном этапе его экономического развития, изменения климата в конкретном пункте земного шара на основе многолетних наблюдений средней температуры воздуха и др.

Однако для того, чтобы средний показатель был действительно типизирующим, он должен определяться не для любых совокупностей, а только для совокупностей, состоящих из качественно однородных единиц. Это является основным условием научно обоснованного использования средних.

Средние, полученные для неоднородных совокупностей, будут искажать характер изучаемого общественного явления, фальсифицировать его или будут бессмысленными. Так, если рассчитать средний уровень доходов служащих какого-либо района, то получится фиктивный средний показатель, поскольку для его исчисления использована неоднородная совокупность, включающая в себя служащих предприятий различных типов (государственных, совместных, арендных, акционерных), а также органов государственного управления, сферы науки, культуры, образования и т.п. В таких случаях метод средних используется в сочетании с методом группировок, позволяющим выделить однородные группы, по которым и исчисляются типические групповые средние.

Групповые средние позволяют избежать «огульных» средних, обеспечивают сравнение уровней отдельных групп с общим уровнем по совокупности, выявление имеющихся различий и т.д.

Однако нельзя сводить роль средних только к характеристике типических значений признаков в однородных по данному признаку совокупностях. На практике современная статистика использует так называемые системные средние, обобщающие неоднородные явления (характеристики государства, единой народнохозяйственной системы: например, средний национальный доход на душу населения, средняя урожайность зерновых по всей стране, средний реальный доход на душу населения, среднее потребление продуктов питания на душу населения, производительность общественного труда).

В современных условиях развития рыночных отношений в экономике средние служат инструментом изучения объективных закономерностей социально-экономических явлений. Однако в экономическом анализе нельзя ограничиваться лишь средними показателями, так как за общими благоприятными средними могут скрываться и крупные серьезные недостатки в деятельности отдельных хозяйствующих субъектов, и ростки нового, прогрессивного. Так, например, распределение населения по доходу позволяет выявлять формирование новых социальных групп. Поэтому наряду со средними статистическими данными необходимо учитывать особенности отдельных единиц совокупности.

Средняя должна исчисляться для совокупности, состоящей из достаточно большого числа единиц, так как в этом случае, согласно закону больших чисел, взаимопогашаются случайные, индивидуальные различия между единицами и они не оказывают существенного влияния на среднее значение, что способствует проявлению основного, существенного, присущего всей массе. Если основываться на средней из небольшой группы данных, то можно сделать неправильные выводы, поскольку такой средний показатель будет отражать значительное влияние индивидуальных особенностей, т.е. случайных моментов, не характерных для изучаемой совокупности в целом.

Каждая средняя характеризует изучаемую совокупность по какому-либо одному признаку, но для характеристики любой совокупности, описания ее типических черт и качественных особенностей нужна система средних показателей. Поэтому в практике отечественной статистики для изучения социально-экономических явлений, как правило, исчисляется система средних показателей. Так, например, показатели средней заработной платы оцениваются совместно с показателями средней выработки, фондовооруженности и энерговооруженности труда, степенью механизации и автоматизации работ и др.

Средняя должна вычисляться с учетом экономического содержания исследуемого показателя. Поэтому для конкретного показателя, используемого в социально-экономическом анализе, можно исчислить только одно истинное значение средней на базе научного способа расчета.

Средняя арифметическая

 

Наиболее распространенным видом средних является средняя арифметическая. Она применяется в тех случаях, когда объем варьирующего признака для всей совокупности является суммой значений признаков отдельных ее единиц. Для общественных явлений характерна аддитивность (суммарность) объемов варьирующего признака, этим определяется область применения средней арифметической и объясняется ее распространенность как обобщающего показателя. Так, например, общий фонд заработной платы – это сумма заработных плат всех работников, валовой сбор урожая – сумма произведенной продукции со всей посевной площади.

Чтобы исчислить среднюю арифметическую, нужно сумму всех значений признаков разделить на их число.

Средняя арифметическая применяется в форме простой средней и взвешенной средней. Исходной, определяющей, формой служит простая средняя.

– Средняя арифметическая простая равна простой сумме отдельных значений осредняемого признака, деленной на общее число этих значений (она применяется в тех случаях, когда имеются несгруппированные индивидуальные значения признака):

 

 

где х₁, х₂, …, х_n – индивидуальные значения варьирующего признака (варианты); n – число единиц совокупности.

Например, требуется найти среднюю выработку одного рабочего (слесаря), если известно, сколько деталей изготовил каждый из 15 рабочих, т.е. дан ряд индивидуальных значений признака, шт.:

21; 20; 20; 19; 21; 19; 18; 22; 19; 20; 21; 20; 18; 19; 20.

 

 

Средняя из вариантов, которые повторяются различное число раз или, как говорят, имеют различный вес, называется взвешенной. В качестве весов выступают численности единиц в разных группах совокупности (в группу объединяют одинаковые варианты).

– Средняя арифметическая взвешенная – средняя сгруппированных величин х₁, Х₂,..., х_n – вычисляется по формуле:

 

 

где f₁, f₂,..., f_n – веса (частоты повторения одинаковых признаков);

Σxf – сумма произведений величины признаков на их частоты;

Σf – общая численность единиц совокупности.

Технику вычисления средней арифметической взвешенной проиллюстрируем на рассмотренном выше примере. Для этого сгруппируем исходные данные и поместим их в табл. 5.1.

Таблица 5.1

 

Средняя гармоническая

 

При расчете средних показателей помимо средней арифметической могут использоваться и другие виды средних. Однако любая средняя величина должна вычисляться так, чтобы при замене ею каждого варианта осредняемого признака не изменялся итоговый, обобщающий, или, как его принято называть, определяющий показатель, который связан с осредняемым показателем (например, при замене фактических скоростей на отдельных отрезках пути их средней скоростью не должно измениться общее расстояние, пройденное транспортным средством за одно и то же время; при замене фактических заработных плат отдельных работников предприятия средней заработной платой не должен измениться фонд заработной платы). Следовательно, в каждом конкретном случае в зависимости от характера имеющихся данных существует только одно истинное среднее значение показателя, адекватное свойствам и сущности изучаемого социально-экономического явления.

Вид средней определяется характером взаимосвязи определяющего показателя с осредняемым.

Средняя арифметическая, как было показано выше, применяется в тех случаях, когда известны варианты варьирующего признака х и их частоты f.

Когда статистическая информация не содержит частот f по отдельным вариантам х совокупности, а представлена как их произведение x ∙ f, применяется формула средней гармонической взвешенной. Чтобы исчислить среднюю, обозначим x ∙ f = w, откуда f = w / x. Теперь преобразуем формулу средней арифметической таким образом, чтобы по имеющимся данным х и w можно было исчислить среднюю. В формулу средней арифметической взвешенной (5.4) вместо xf подставим w, вместо f – отношение w / x и получим формулу средней гармонической взвешенной:

 

 

Из формулы (5.9) видно, что средняя гармоническая – средняя взвешенная из варьирующих обратных значений признака. Она является преобразованной формой арифметической средней и тождественна ей. Вместо гармонической всегда можно рассчитать среднюю арифметическую, но для этого сначала нужно определить веса отдельных значений признака, скрытые в весах средней гармонической.

Таким образом, средняя гармоническая применяется тогда, когда неизвестны действительные веса f, а известно w = x ∙ f, т.е. в тех случаях, когда средняя предназначается для расчета сумм слагаемых, обратно пропорциональных величине данного признака, когда суммированию подлежат не сами варианты, а обратные им величины.

Например, по данным табл. 5.5 требуется определить среднюю цену 1 кг яблок в апреле.

Таблица 5.5

Средняя геометрическая

 

Средняя геометрическая применяется в тех случаях, когда индивидуальные значения признака представляют собой, как правило, относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики, т.е. характеризует средний коэффициент роста.

Средняя геометрическая исчисляется извлечением корня степени n из произведений отдельных значений – вариантов признака х:

 

 

где n – число вариантов; П – знак произведения.

Наиболее широкое применение средняя геометрическая получила для определения средних темпов изменения в рядах динамики, а также в рядах распределения.

Использование средней геометрической показано в гл. 7.

Структурные средние

 

Особым видом средних величин являются структурные средние. Они применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К таким показателям относятся мода и медиана.

– Мода M₀ – значение случайной величины, встречающееся с наибольшей вероятностью в дискретном вариационном ряду – вариант, имеющий наибольшую частоту.

Например, в табл. 5.1 наибольшей частотой является число 5. Этой частоте соответствует модальное значение признака, т.е. выработка деталей за смену. Мода свидетельствует, что в данном примере чаще всего встречаются рабочие, изготавливающие за смену 20 деталей.

В интервальных рядах распределения с равными интервалами мода вычисляется по формуле:

 

 

Модальный интервал определяется по наибольшей частоте.

По данным табл. 5.4 рассчитаем моду:

 

 

Итак, модальным значением стоимости ОПФ предприятий региона является стоимость, равная 18,8 млн руб.

Мода широко используется в статистической практике при изучении покупательского спроса, регистрации цен и т.п.

– Медиана М_е – это вариант, который находится в середине вариационного ряда. Медиана делит ряд на две равные (по числу единиц) части – со значениями признака меньше медианы и со значениями признака больше медианы. Чтобы найти медиану, необходимо отыскать значение признака, которое находится в середине упорядоченного ряда. В ранжированных рядах несгруппированных данных нахождение медианы сводится к отысканию порядкового номера медианы.

Пусть ряд состоит из показателей заработной платы 9 рабочих, руб./мес. (в 1996 г.):

630, 650, 680, 690, 700, 710, 720, 730, 750.

Номер медианы для нечетного объема вычисляется по формуле:

 

 

где n – число членов ряда.

В нашем примере номер медианы равен 5, медиана равна 700 руб. (т.е. одна половина рабочих получила заработную плату менее 700 руб., а другая – более 700 руб. в месяц).

В случае четного объема ряда медиана равна средней из двух вариантов, находящихся в середине ряда.

В интервальных рядах распределения медианное значение (поскольку оно делит всю совокупность на две равные по численности части) оказывается в каком-то из интервалов признака х. Этот интервал характерен тем, что его кумулятивная частота (накопленная сумма частот) равна или превышает полусумму всех частот ряда. Значение медианы вычисляется линейной интерполяцией по формуле:

 

 

Формула (5.17) получена исходя из допущения о равномерности нарастания накоплений частоты внутри интервала и пригодна для любого интервальног