
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Показатели ряда динамики и методы их исчисления.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Исходные значения признака, образующие динамический ряд, называются уровнями ряда. Тот уровень, который является базой для сравнения и с которым производится сравнение других уровней, называется базисным. За базу сравнения применяют либо начальный (первый), либо предыдущий, или любой, выбранный за базу сравнения уровень динамического ряда. Базисный уровень в статистике обычно принято обозначать У0. Уровень ряда, который сравнивается с базисным, называется текущим (отчетным). Текущие уровни могут иметь следующие обозначения: У1, У2, У3…Уn. Если все уровни динамического ряда сравниваются с одним и тем же уровнем, то полученные показатели динамики называются базисными. Если же каждый последующий уровень ряда сравнивается с каждым предыдущим, то полученные динамические показатели называются цепными. Эти показатели представляют собой как бы отдельные звенья единой «цепи», связывающей между собой уровни ряда. В динамическом ряду приводится несколько последовательных уровней, среди которых особый интерес представляют начальный, срединный и конечный уровни ряда. Первый член динамического ряда называется начальным уровнем. Срединный уровень ряда находится по способу определения медианы. Последний член динамического ряда принято называть конечным. Для общей характеристики явления за весь период целесообразно рассчитать средний уровень из всех членов динамического ряда. При этом способ расчета среднего уровня зависит от вида динамического ряда. При расчете среднего уровня в моментном динамическом ряду (с равными промежутками между моментами) рекомендуется использовать способ средней хронологической простой величины. В тех случаях, когда моментный ряд динамики представлен неравными промежутками между датами, средний уровень ряда обычно рассчитывают по способу средней арифметической взвешенной. При расчете среднего уровня в периодическом ряду динамики обычно рекомендуются использовать способ средней арифметической простой величины. Одним из наиболее простых показателей развития динамики является абсолютный прирост уровня. Абсолютным приростом называется разность двух уровней динамического ряда. Абсолютный прирост измеряется в тех же единицах, в которых показаны абсолютные уровни ряда динамики. Если абсолютный прирост уровня обозначим через ΔУ, уровень последующего периода – Уi, уровень предыдущего периода – Уi-1, то значение абсолютного прироста алгебраически может быть выражено следующим образом:
где Абсолютный прирост выражает абсолютное изменение уровней и показывает, на сколько единиц увеличился или уменьшился последующий уровень динамического ряда по сравнению с предыдущим. Средний абсолютный прирост всегда является периодическим показателем. Поэтому он исчисляется по формуле простой средней арифметической из цепных абсолютных приростов за последовательные и более-менее равные по продолжительности периоды: где n – число цепных абсолютных приростов. Согласно первой зависимости общая сумма цепных абсолютных приростов (ΣΔУц) ряда динамики представляет собой базисный абсолютный прирост за весь изучаемый период в целом (Уn – У0). Число приростов (n) равно числу уровней ряда минус единица где Уп – значение конечного уровня динамического ряда; У0 – начальный уровень ряда; m – число уровней ряда. Для характеристики относительной скорости изменения уровня динамического ряда используется показатель темпа роста. Темп роста –– это отношение одного уровня динамического ряда к другому, принятому за базу сравнения. Темпы роста могут быть выражены в форме коэффициентов или процентов. Коэффициент роста показывает, во сколько раз сравниваемый (текущий) уровень больше базисного:
где К – коэффициент роста уровней; Уi – уровень последующего периода; Уi-1 – уровень предыдущего периода. Коэффициент роста, выраженный в процентах, называется темпом:
Темпы роста могут быть рассчитаны базисным и цепным способами. Между базисными и цепными темпами роста, выраженными в форме коэффициентов, имеется определенная взаимосвязь, которая заключается в следующем: Во-первых, произведение последовательных цепных темпов роста равно базисному темпу роста за соответствующий период; Во-вторых, частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста. Указанные зависимости между темпами роста можно использовать для преобразования базисных темпов в цепные и наоборот, особенно в тех случаях, когда неизвестны абсолютные уровни динамики. В отличие от абсолютного прироста за весь период, который представляет собой сумму абсолютных приростов за каждый отдельный промежуток времени, общий показатель темпа роста –– это произведение цепных коэффициентов (темпов) роста за каждый промежуток времени, т.е. коэффициенты связаны между собой знаком произведения. Поэтому для определения средних темпов роста необходимо применить среднюю геометрическую простую: где К1, К2, К3….Кn –– цепные коэффициенты роста за каждый отдельный промежуток времени; n –– число темпов роста. Если произведение цепных темпов заменить соответствующим базисным темпом роста за весь изучаемый период, то получим формулу среднего темпа роста, имеющую следующий вид: где Уп –– конечный уровень ряда; У0 –– начальный уровень; п –– число уровней в динамическом ряду. Если абсолютная скорость прироста уровней динамического ряда характеризуется величиной абсолютных приростов, то относительная скорость прироста уровней – темпами прироста. Темп прироста представляет собой отношение абсолютного прироста к уровню, принятому за базу. Темпы прироста, как и темпы роста, могут быть выражены в форме коэффициентов и процентов. Коэффициент прироста показывает, на какую долю увеличился или уменьшился последующий уровень по сравнению с предыдущим, т.е. где ΔК – коэффициент прироста уровня, выраженный в долях; ΔУ – абсолютный прирост уровня; Уi-1 – предыдущий уровень. Темп прироста, выраженный в процентах показывает, на сколько процентов увеличился или уменьшился последующий уровень по сравнению с предыдущим, т.е. Темпы прироста также, как и темпы роста, могут быть рассчитаны базисным и цепным способами. Между темпами прироста и темпами роста существует непосредственная связь. Поэтому коэффициент (темп) прироста можно выразить через темп роста, т.е. Абсолютное значение одного процента прироста представляет собой отношение абсолютного прироста к темпу прироста, выраженному в процентах где 1 % ΔУ – абсолютное значение 1 % прироста; ΔУ – абсолютный прирост уровня; ΔТ – темп прироста, %. После несложного преобразования формулы получим, что
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 982; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.247.17 (0.008 с.) |

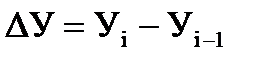 (1)
(1) .
.
 – средний абсолютный прирост;
– средний абсолютный прирост; . Следовательно, средний абсолютный прирост можно выразить в следующе
. Следовательно, средний абсолютный прирост можно выразить в следующе 
 (6)
(6)

 –– средний коэффициент роста за весь период;
–– средний коэффициент роста за весь период;
 –– средний темп роста;
–– средний темп роста; ,
, .
. , или
, или  .
.
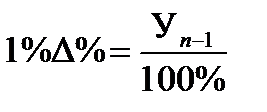 .
.


