
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 5. Показатели вариацииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Основные понятия Исследование вариации в статистике и социально-экономических исследованиях имеет важное значение, так как величина вариации признака в статистической совокупности характеризует ее однородность. Вариация – различие значений какого-либо признака у разных единиц совокупности за один и тот же промежуток времени. В статистической практике для изучения и измерения вариации используют различные показатели (меры) вариации в зависимости от поставленных задач. Так, к абсолютным показателям вариации относятся размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, дисперсия. Относительные показатели вариации - это коэффициенты осцилляции, вариации, относительное линейное отклонение и др. Размах вариации (R) является наиболее простым измерителем вариации признака. Он определяется какразность между наибольшим и наименьшим значением вариантов.
где Среднее линейное отклонение (
Символы Дисперсия представляет собой средний квадрат отклонений индивидуальных значений от их средней величины (обозначается греческой буквой
Как и любая средняя, дисперсия имеет определенные математические свойства: а) если из всех значений вариации отнять какое то постоянное число К, то дисперсия от этого не изменится; б) если все значения вариации разделить на какое то постоянное число К, то дисперсия уменьшиться в К² раз; в) в случае замены частот долями дисперсия не изменится; г) если исчислить средний квадрат отклонений от любой величины K, которая в той или иной степени отличается от средней арифметической
А именно средний квадрат отклонений при этом будет больше на квадрат разности средней и этой условно взятой величиной, т.е. на
или
Среднее квадратическое отклонение представляет собой корень квадратный из среднего квадрата отклонений отдельных значений признака от их средней:
Среднее квадратическое отклонение – величина именованная, имеет размерность осредняемого признака. Расчет дисперсии прямым способом в ряде случаев трудоемок. Упростить ее вычисления можно, используя расчет дисперсии по способу отсчета от условного нуля или способу моментов по следующей формуле:
Формула расчета дисперсии по способу моментов имеет следующий вид:
где k – величина интервала; А – условный нуль, в качестве которого используют середину интервала с наибольшей частотой;
В случае, когда А приравнивается к нулю и, следовательно, не вычисляются отклонения, формула принимает вид:
Для целей сравнения колебания различных признаков в одной и той же совокупности или же при сравнении колебаний одного и того же признака в нескольких совокупностях вычисляются относительные показатели вариации. Базой для сравнения служит средняя арифметическая. Эти показатели вычисляются как отношение размаха, или среднего линейного отклонения, или среднего квадратического отклонения к средней арифметической. Чаще всего они выражаются в процентах и характеризуют не только сравнительную оценку вариации, но и дают характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33 %. Различают следующие относительные показатели вариации: - коэффициент осцилляции – процентное отношение размаха вариации к средней величине признака:
- линейный коэффициент вариации – процентное отношение среднего линейного отклонения к средней величине признака:
- коэффициент вариации – процентное отношение среднего квадратического отклонения к средней величине признака:
Наряду с изучением вариации признака по всей совокупности в целом часто бывает необходимо проследить количественные изменения признака по группам, на которые разделяется совокупность, а также между группами. Такое изучение вариации достигается посредством вычисления и анализа различных видов дисперсии. Если данные представлены в виде аналитической группировки, то можно вычислить дисперсию общую, межгрупповую и внутригрупповую. Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию:
Межгрупповая дисперсия характеризует систематическую вариацию, т. е. различия в величине изучаемого признака, возникающие под действием признака – фактора, положенного в основание группировки. Она рассчитывается по формуле:
где Внутригрупповая дисперсия отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака–фактора, положенного в основание группировки. Она исчисляется следующим образом:
Средняя из внутригрупповых дисперсий:
Существует закон, связывающий три вида дисперсий. Общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий:
Данное соотношение называют правилом сложения дисперсий. Согласно этому правилу, общая дисперсия, возникающая под влиянием всех факторов, равна сумме дисперсий, возникающих под влиянием всех прочих факторов, и дисперсии, возникающей за счет группировочного признака. Зная любые два вида дисперсий, можно определить или проверить правильность расчета третьего вида. Тест Выберите правильный ответ. 1. Вариация – это: а) изменение массовых явлений во времени; б) изменение структуры статистической совокупности в пространстве; в) изменение значений признака во времени и в пространстве; г) изменение состава совокупности. 2. К абсолютным показателям вариации не относятся: а) коэффициент вариации; б) размах вариации; в) дисперсия; г) коэффициент осцилляции; д) среднее квадратическое отклонение; е) среднее линейное отклонение. 3. Коэффициент вариации рассчитывается по формуле:
4. Если все значения признака уменьшить или увеличить на какое-то постоянное число, то дисперсия от этого не изменится:
5. Показатель вариации, характеризующий долю усредненного значения абсолютных отклонений от средней величины, носит название: а) коэффициент осцилляции; б) относительное линейное отклонение; в) коэффициент вариации. 6. Для расчета среднего квадратического отклонения (взвешенного) используется следующая формула:
7. Если все значения признака уменьшить на 3, то величина дисперсии: а) не изменится; б) уменьшится на 3; в) увеличится на 3; г) уменьшится на 9; д) увеличится на 9; е) предсказать изменение дисперсии нельзя. 8. Межгрупповая дисперсия характеризует: а) вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию; б) систематическую вариацию, т. е. различия в величине изучаемого признака, возникающие под действием признака-фактора, положенного в основание группировки; в) случайную вариацию, т. е. часть вариации, происходящую под влиянием неучтенных факторов и независящую от признака-фактора. 9. Правило сложения дисперсий гласит: а) общая дисперсия равна сумме межгрупповой дисперсии и внутригрупповых дисперсий; б) общая дисперсия, возникающая под влиянием всех факторов, равна сумме дисперсии, появляющейся под влиянием всех прочих факторов, и дисперсии, возникающей за счет группировочного признака. 10. Если отсутствуют различия между вариантами внутри групп, межгрупповая дисперсия равна: а) единице; б) нулю; в) колеблется от нуля до единицы; г) общей дисперсии; д) средней из групповых дисперсий. 11. Разница между максимальным и минимальными значениями признака носит название: а) среднее линейное отклонение; б) размах вариации; в) дисперсия. Задачи Примеры решения задач Пример 1. На основе данных таблицы 5.1 (графы 1, 2) рассчитаем дисперсию и среднее квадратическое отклонение для интервального ряда распределения. Таблица 5.1– Распределение магазинов города по товарообороту во 2-м квартале 2010 г.
Решение: При расчете показателей вариации по интервальным рядам распределения необходимо сначала определить середины интервалов, а затем вести дальнейшие расчеты, рассматривая ряд середин интервалов как дискретный вариационный ряд распределения. Результаты вспомогательных расчетов для определения дисперсии и среднего квадратического отклонения содержатся в графах (3-6) таблицы 5.1. Средний размер товарооборота определяется по средней арифметической взвешенной и составляет:
Дисперсия товарооборота:
Среднее квадратическое отклонение товарооборота определяется как корень квадратный из дисперсии:
Воспользуемся данными таблицы 5.1 и рассчитаем дисперсию по способу моментов и способу отсчета от условного нуля (табл. 5.2).
Таблица 5.2 – Расчет дисперсии способом отсчета от условного нуля
По способу отсчета от условного нуля:
По способу моментов получаем:
Разница в расчетах дисперсий получена в связи с округлением средней величины до целого числа. В идеале значения дисперсии, рассчитанной различными способами по одним и тем же данным, должны совпадать.
Пример 2. Определим групповые дисперсии, среднюю из групповых дисперсий, межгрупповую дисперсию, общую дисперсию по данным табл. 5.3.
Таблица 5.3 – Производительность труда двух бригад
Решение: для расчета групповых дисперсий вычислим среднее по каждой группе:
Промежуточные расчеты дисперсий по группам представлены в табл. 5.3. Подставив полученные значения в формулу, получим:
Средняя из групповых дисперсий:
Для расчета межгрупповой дисперсии определяем общую среднюю как среднюю взвешенную из групповых дисперсий:
Межгрупповая дисперсия:
Таким образом, общая дисперсия по правилу сложения дисперсий равна:
Проверим полученный результат:
Задачи 1. Распределение студентов одного из факультетов по возрасту характеризуется следующими данными (табл. 5.5).
Таблица 5.5 – Распределение студентов экономического факультета ОрелГТУ по возрасту на 1.09.2010 г.
Вычислите: а) размах вариации; б) среднее линейное отклонение; в) дисперсию; г) среднее квадратическое отклонение; д) относительные показатели вариации возраста студентов.
2. По данным, представленным в таблице 5.6, определите среднюю длину пробега автофургона торгово-посреднической фирмы и вычислите все показатели вариации.
Таблица 5.6 – Распределение рейсов ООО «Металлснаб» за 1-й квартал 2010 г. по длине пробега за один рейс
3. Имеется следующий ряд распределения телеграмм, принятых отделением связи, по числу слов (табл. 5.7).
Таблица 5.7 – Распределение телеграмм, принятых Орловским отделением связи за январь 2010 г., по числу слов
Рассчитайте абсолютные и относительные показатели вариации.
4. Средний доход предприятий промышленности в двух районах характеризуется следующими данными (табл. 5.8).
Таблица 5.8 – Средний доход предприятий промышленности в двух районах за 2007–2011 гг. (усл. ед.)
1. Рассчитайте все показатели вариации. 2. Определите, в каком районе доход предприятий больше.
5. Имеются следующие данные выборочного обследования студентов Орловского государственного технического университета (табл. 5.9).
Таблица 5.9 – Распределение студентов ОрелГТУ по затратам времени на дорогу до университета на 1.10.10 г.
Вычислите абсолютные и относительные показатели вариации. Расчеты оформите в табличной форме. Сделайте выводы.
6. Акционерные общества (АО) области по среднесписочной численности работающих на 1 января 2008 г. распределялись следующим образом (табл. 5.10).
Таблица 5.10 – Распределение акционерных обществ области по среднесписочной численности работающих на 1.01.11 г.
Рассчитайте: а) среднее линейное отклонение; б) дисперсию; в) среднее квадратическое отклонение; г) коэффициент вариации.
7. По данным о распределении коммерческих банков по размеру чистой прибыли за 2010 г. (табл. 5.11) вычислите общую дисперсию тремя способами.
Таблица 5.11– Распределение коммерческих банков по размеру чистой прибыли за 2010 г.
8. По имеющимся данным о распределении сотрудников коммерческого банка по среднемесячной заработной плате (табл. 5.12) определите общую дисперсию тремя способами.
Таблица 5.12 – Распределение сотрудников филиала «Орловский» АКБ «Агростройбанк» по среднемесячной заработной плате на 1.08.11 г.
9. Средняя величина признака в совокупности равна 19, а средний квадрат индивидуальных значений этого признака – 397. Определите коэффициент вариации.
10. Дисперсия признака равна 9, средний квадрат индивидуальных его значений – 130. Чему равна средняя?
11. Средняя величина в совокупности равна 16, среднее квадратическое отклонение – 8. Определите средний квадрат индивидуальных значений этого признака.
12. Средний квадрат отклонений индивидуальных значений признака от их средней величины равен 100, а средняя – 15. Определите, чему равен средний квадрат отклонений индивидуальных значений признака от величины, равной 10 и 25.
13. Средняя величина признака равна 14, а дисперсия – 60. Определите средний квадрат отклонений вариантов признака от 19.
14. Средний квадрат отклонений вариантов признака от произвольной величины равен 300, а сама произвольная величина равна 70 единицам. Определите дисперсию признака, если известно, что средняя величина его варианта равна 80.
15. Товарооборот по предприятиям розничной торговли на одного работника характеризуется следующими данными (табл. 5.13).
Таблица 5.13 – Товарооборот по предприятиям розничной торговли на одного работника на 1.10.2010 г.
Определите все виды дисперсий товарооборота предприятий общественного питания.
16. В таблице 5.14 представлены данные о распределении семей сотрудников финансовой корпорации по количеству детей.
Таблица 5.14 – Распределение семей сотрудников финансовой корпорации по количеству детей на 1.01.2010 г.
Определите: а) внутригрупповые дисперсии; б) среднюю из внутригрупповых дисперсий; в) межгрупповую дисперсию; г) общую дисперсию. Проверьте правильность произведения расчетов с помощью правила сложения дисперсий.
Глава 6. Ряды динамики Основные понятия Динамика – процесс развития движения социально экономического явления во времени.Для отображения динамики строят ряды динамики. Ряд динамики – ряд числовых значений определенного статистического показателя в последовательные моменты времени или периоды времени. Составляющими ряда динамики являются признак времени (t) (момент или интервал) и числовые значения показателя – уровни ( Интервальный ряд динамики – ряд числовых значений определенного статистического показателя, характеризующего размеры изучаемого явления за определенные промежутки (периоды, интервалы) времени. Моментный ряд динамики – ряд числовых значений определенного статистического показателя, характеризующего размеры изучаемого явления на определенные даты, моменты времени. Примеры указанных рядов приведены в таблице 6.1, где поквартальные объемы экспорта товаров – это интервальный ряд, а суммы резервов иностранной валюты на конец квартала – моментный ряд.
Таблица 6.1 Объем экспорта и резервы иностранной валюты за 2009 – 2010 гг.
Одним из важнейших направлений анализа рядов динамики является изучение особенностей развития явления за отдельные периоды времени. Для выявления специфики развития изучаемых явлений за отдельные периоды времени определяют абсолютные и относительные показатели изменения ряда динамики: абсолютные приросты, абсолютное значение одного процента прироста, темпы роста и прироста. Рассматривая данные показатели, необходимо правильно выбирать базу сравнения, которая зависит от цели исследования. При сравнении каждого уровня с предыдущим получают цепные показатели; при сравнении каждого уровня с одним и тем же уровнем (базой) - базовые показатели. Абсолютный прирост (
где
Темп роста (
Темп прироста (
Темп прироста может быть вычислен также путем вычитания из темпов роста 100 %:
Показатель абсолютного значения одного процента прироста (|%|) определяется как результат деления абсолютного прироста на соответствующий темп прироста, выраженный в процентах:
Расчет этого показателя имеет смысл только на цепной основе. Средние показатели рядов динамики являются обобщающей характеристикой их абсолютных уровней, абсолютной скорости и интенсивности изменения уровней ряда динамики. Различают следующие средние показатели: средний уровень ряда динамики, средний абсолютный прирост, средний темп роста и прироста. Методы расчета среднего уровня ряда динамики зависят от его вида и способов получения статистических данных. В интервальном ряду динамики с равноотстоящими уровнями во времени расчет среднего уровня ряда (
Для интервального ряда динамики с неравноотстоящими уровнями средний уровень ряда вычисляется по формуле:
где t – число периодов времени, в течение которых уровень не изменяется. Для моментного ряда с равноотстоящими уровнями средний уровень ряда рассчитывается по формуле средней хронологической:
где n – число уровней ряда. Средний уровень моментного ряда с разноотстоящими уровнями вычисляется по следующей формуле:
Средний абсолютный прирост – показатель, характеризующий среднюю абсолютную скорость роста (снижения) уровня за отдельные периоды времени. Он показывает, на сколько единиц увеличился (уменьшился) уровень по сравнению с предыдущим в среднем за единицу времени (в среднем ежегодно, ежемесячно и т.д.). Определение среднего абсолютного прироста производится по формуле:
Средний темп роста – относительный показатель, выраженный в форме коэффициента и показывающий, во сколько раз увеличился уровень по сравнению с предыдущим в среднем за единицу времени (в среднем ежегодно, ежеквартально и т.п.). Среднегодовой темп роста вычисляется по формуле средней геометрической:
где m – число коэффициентов роста. Средний темп прироста – относительный показатель, выраженный в процентах и показывающий, на сколько увеличился (уменьшился) уровень по сравнению с предыдущим в среднем за единицу времени (в среднем ежегодно, ежемесячно и т.п.). Среднегодовой темп прироста получаем, вычтя из среднего темпа роста 100 %:
Важной задачей статистики при анализе рядов динамики является определение основной тенденции развития. Основная тенденция (тренд) – достаточно плавное и устойчивое изменение уровня явления во времени, более или менее свободное от случайных колебаний. Основную тенденцию можно представить либо аналитически – в виде уравнения (модели) тренда, либо графически. Механическое сглаживание – метод нахождения плавных уровней ряда путем использования скользящих средних. Аналитическое выравнивание динамического ряда проводится при помощи математической формулы, отражающей общую тенденцию ряда. Тест
Выберите правильный ответ: 1. Ряды динамики – это: а) количественная характеристика социально-экономических явлений; б) количественные изменения величины исследуемого признака в пределах однородной совокупности; в) статистические данные, отображающие развитие изучаемого явления во времени. 2. Уровень ряда динамики – это: а) определенное значение варьирующего признака в совокупности; б) величина показателя на определенную дату или момент времени; в) величина показателя за определенный период времени; г) б, в. 3. Средний уровень интервального ряда динамики определяется как: а) средняя арифметическая; б) средняя гармоническая; в) средняя хронологическая. 4. Средний уровень моментного ряда определяется как средняя арифметическая взвешенная при: а) равноотстоящих уровнях между датами; б) неравноотстоящих уровнях между датами. 5. Если сравниваются смежные уровни ряда динамики, показатели называются: а) цепными; б) базисными. 6. Для преодоления несопоставимости рядов используют: а) среднюю хронологическую; б) коэффициент пересчета; в) смыкание рядов. 7. Абсолютный прирост исчисляется как: а) отношение уровней; б) разность уровней ряда. 8. Укажите, с помощью какого выражения исчисляется средний уровень ряда динамики ( а) б) в) г) 9. Темп роста исчисляется как: а) отношение уровней ряда; б) разность уровней ряда. 10. Основная тенденция представляет собой изменение ряда динамики: а) равномерно повторяющееся через определенные промежутки времени внутри ряда; б) определяющее какое-то общее направление развития. 11. Сравниваемый уровень ряда динамики называется: а) отчетным; б) плановым; в) базисным 12. Базисный абсолютный прирост ( а) б) в) 13. При построении рядов динамики необходимо соблюдать следующие требования: а) для всесторонней характеристики развития изучаемых явлений необходима система существующих статистических показателей
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 1468; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |



 – наибольшее и наименьшее значение варьирующего признака.
– наибольшее и наименьшее значение варьирующего признака.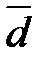 ) представляет собой среднюю величину из отклонений вариантов признака от их средней. Его можно рассчитать по формуле средней арифметической, как невзвешенной, так и взвешенной, в зависимости от отсутствия или наличия частот в ряду распределения:
) представляет собой среднюю величину из отклонений вариантов признака от их средней. Его можно рассчитать по формуле средней арифметической, как невзвешенной, так и взвешенной, в зависимости от отсутствия или наличия частот в ряду распределения: – невзвешенное среднее линейное отклонение;
– невзвешенное среднее линейное отклонение; – взвешенное среднее линейное отклонение.
– взвешенное среднее линейное отклонение. и
и  имеют то же значение, что и в предыдущей главе. Рассмотренные выше показатели имеют ту же размерность, что и признак, для которого они вычисляются.
имеют то же значение, что и в предыдущей главе. Рассмотренные выше показатели имеют ту же размерность, что и признак, для которого они вычисляются. – «сигма квадрат»). Дисперсия вычисляется по формулам простой невзвешенной и взвешенной:
– «сигма квадрат»). Дисперсия вычисляется по формулам простой невзвешенной и взвешенной: – невзвешенная;
– невзвешенная; – взвешенная.
– взвешенная. , то он всегда будет больше среднего квадрата отклонений s², исчисленный от средней арифметической:
, то он всегда будет больше среднего квадрата отклонений s², исчисленный от средней арифметической: .
. :
:
 .
. – невзвешенное;
– невзвешенное; – взвешенное.
– взвешенное. .
. ,
,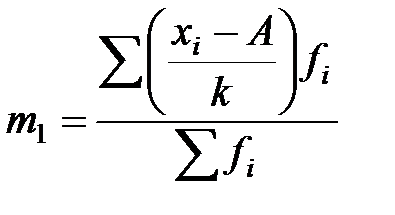 – начальный момент первого порядка;
– начальный момент первого порядка; – начальный момент второго порядка.
– начальный момент второго порядка.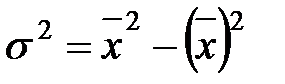 или
или 
 %,
%, %,
%, %.
%. .
.

 – соответственно средние и численности по отдельным группам.
– соответственно средние и численности по отдельным группам.


 ;
;
 ;
;
 ;
;
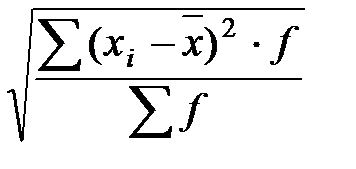 ;
;
 ;
;
 .
.





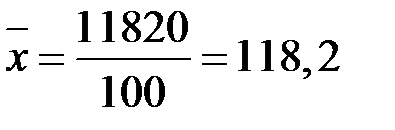 тыс. руб.
тыс. руб. тыс. руб.
тыс. руб. тыс. руб.
тыс. руб.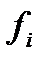

 (А = 115)
(А = 115)
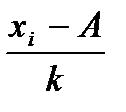 (k = 10)
(k = 10)










 шт.;
шт.; шт.
шт.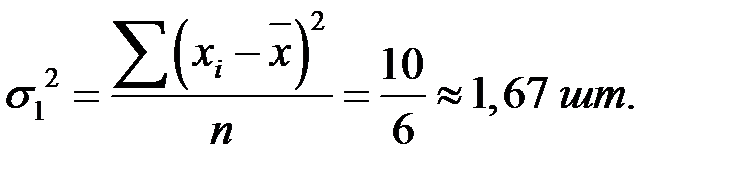 ;
;
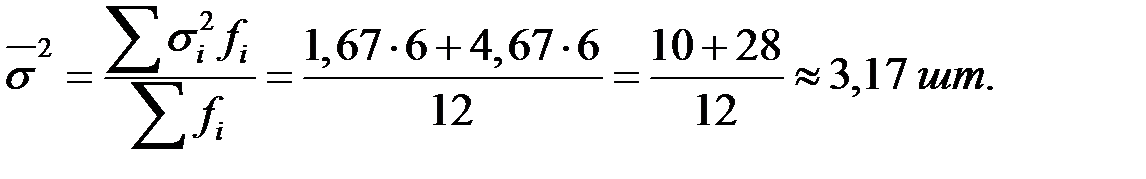
 шт.
шт.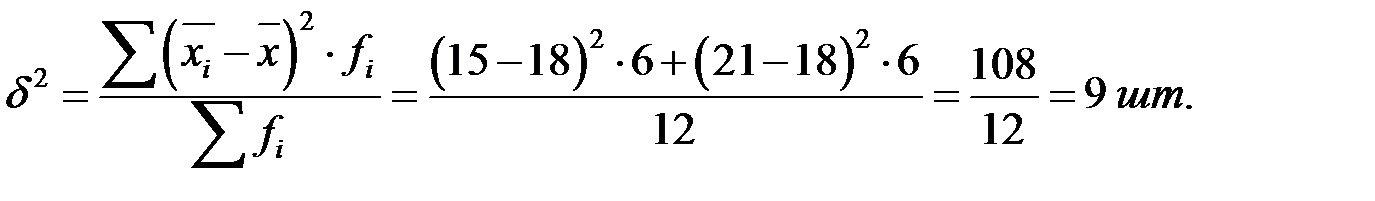


 ). В соответствии с классификацией показателей по признаку времени ряды динамики делятся на моментные и интервальные.
). В соответствии с классификацией показателей по признаку времени ряды динамики делятся на моментные и интервальные. ) измеряет абсолютную скорость роста (или снижения) уровня ряда за единицу времени (месяц, квартал, год и т.д.). Он показывает, на сколько единиц увеличивается или уменьшается уровень по сравнению с базисным, т.е. за тот или иной промежуток времени. Его величина определяется как разность двух сравниваемых уровней:
) измеряет абсолютную скорость роста (или снижения) уровня ряда за единицу времени (месяц, квартал, год и т.д.). Он показывает, на сколько единиц увеличивается или уменьшается уровень по сравнению с базисным, т.е. за тот или иной промежуток времени. Его величина определяется как разность двух сравниваемых уровней: или
или 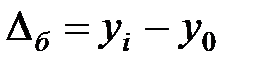 ,
, – уровень i -го года;
– уровень i -го года; – уровень базисного года.
– уровень базисного года. ) – относительный показатель, характеризующий интенсивность процесса роста (снижения). Он показывает, сколько процентов составляет уровень данного периода по сравнению с базисным или предыдущим уровнем, т.е. характеризует относительную скорость изменения уровня ряда в единицу времени. Он вычисляется по формуле:
) – относительный показатель, характеризующий интенсивность процесса роста (снижения). Он показывает, сколько процентов составляет уровень данного периода по сравнению с базисным или предыдущим уровнем, т.е. характеризует относительную скорость изменения уровня ряда в единицу времени. Он вычисляется по формуле: или
или  .
. ) – относительный показатель, характеризующий величину прироста (снижения) и рассчитываемый как отношение абсолютного прироста к предыдущему или базисному уровню:
) – относительный показатель, характеризующий величину прироста (снижения) и рассчитываемый как отношение абсолютного прироста к предыдущему или базисному уровню: или
или 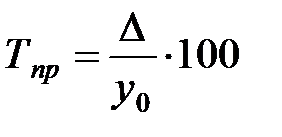 .
.
 или
или 
 ) производится по формуле средней арифметической простой:
) производится по формуле средней арифметической простой: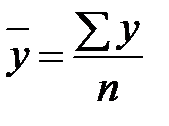 .
.


 или
или 
 , или
, или  ,
, .
. ) в моментных рядах с разноотстоящими датами:
) в моментных рядах с разноотстоящими датами:
 ;
;
 .
. ) определяется по формуле:
) определяется по формуле:





