
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 3. Статистические показателиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Основные понятия Статистическое исследование независимо от его масштабов и целей всегда завершается расчетом и анализом различных по виду и форме выражения статистических показателей. Статистический показатель – количественная характеристика социально-экономических явлений и процессов в условиях качественной определенности. Качественное содержание показателя зависит от сути явления (процесса) и находит свое отражение в названии (рождаемость, прибыльность и т.п.). Количественную сторону явления представляют число и его измеритель. Соединительным звеном между качественным содержанием и числовым выражением является правило построения, модель показателя, которая раскрывает его статистическую структуру, устанавливает, что, где, когда, каким образом подлежит измерению. В ней обосновывают единицы измерения и вычислительные операции. Модель показателя обеспечивает адекватность отображения явления (процесса) и точность его измерения, т.е. оба аспекта достоверности статистической информации. Все статистические показатели по охвату единиц совокупности разделяются на индивидуальные и сводные, а по признаку времени – на интервальные и моментные. Индивидуальные показатели характеризуют отдельный объект или отдельную единицу совокупности – предприятие, фирму, банк и т.п. Сводные показатели характеризуют группу единиц, представляющую собой часть статистической совокупности или всю совокупность в целом. Интервальные показатели характеризуют явление за определенное время (день, месяц, год). Например, ввод в действие жилья, перевозка грузов и т.п. К моментным относят показатели, характеризующие явление на определенный момент времени: протяженность нефтепроводов на конец года, остатки оборотных средств на начало месяца. По форме выражения различают абсолютные, относительные и средние показатели. Абсолютные статистические величины характеризуют размеры социально-экономических явлений – объемы совокупности или объемы значений определенных признаков. В зависимости от конкретной задачи исследования и характера явления используют натуральные, трудовые и стоимостные (денежные) единицы измерения абсолютных величин. Если возникает потребность свести воедино несколько разновидностей одного потребительского свойства, объемы такого явления выражают в условно-натуральных единицах. Пересчет в условные единицы осуществляется посредством специальных коэффициентов-соизмерителей. Относительный показатель характеризует количественные соотношения разноименных или одноименных показателей. Любой относительный показатель представляет собой дробь, числителем которой является сравниваемая величина, а знаменателем – база сравнения. Относительный показатель показывает, во сколько раз сравниваемая величина больше базисной или какую долю она составляет относительно базисной, иногда – сколько единиц одной величины приходится на 100, 1000, 10000, 100000 единиц другой. По аналитической функции выделяют относительные показатели интенсивности, динамики, сравнения, структуры, координации. Относительный показатель интенсивности (ОПИ) характеризует степень распространения явления в определенной среде. Это именуемая величина, в которой объединяются единицы измерения числителя и знаменателя. Например, показатель уровня экономического развития страны – ВВП (дол. США) на душу населения, демографические коэффициенты (рождаемости, смертности) на 1000 чел. населения, обеспеченность врачами на 10000 чел. населения, заболеваемость на 100000 чел. населения. Относительный показатель динамики (ОПД) характеризует направление и интенсивность изменения явления во времени, определяется соотношением значений показателя за два периода или момента времени. При этом базой сравнения может быть или предыдущий уровень, или уровень, более отдаленный во времени.
Относительный показатель сравнения (ОПСр) представляет собой соотношение одного и того же абсолютного показателя, характеризующего разные объекты (предприятия, фирмы, районы области и т.п.).
Относительный показатель структуры (ОПС) характеризует состав, структуру совокупности по тому или иному признаку, определяется отношением размера составной части к общему итогу.
Выражается относительный показатель структуры в долях единицы или в процентах. Рассчитанные величины, соответственно называемые долями или удельными весами, показывают, какой долей обладает или какой удельный вес имеет та или иная часть в общем итоге. Относительный показатель координации (ОПК) представляет собой отношение одной части совокупности к другой части этой же совокупности. При этом в качестве базы сравнения выбирается та часть, которая имеет наибольший удельный вес или является приоритетной с экономической, социальной или какой-либо другой точки зрения. В результате получают, во сколько раз данная часть больше базисной, или сколько процентов от нее составляет, или сколько единиц данной структурной части приходится на единицу (иногда на 100, 1000 и более единиц) базисной структурной части. Тест Выберите правильный ответ. 1. Статистический показатель – это: а) обобщающий показатель, дающий числовую меру соотношения между двумя величинами; б) количественная оценка социально-экономических явлений; в) совокупность статистических данных. 2. Относительный показатель интенсивности развития: а) характеризует соотношение структурных частей изучаемого объекта и их целого; б) характеризует степень распространения изучаемого процесса или явления; в) характеризует напряженность плана. 3. По степени охвата единиц совокупности показатель «Прибыль коммерческого банка» относится к следующему виду: а) индивидуальный; б) сводный. 4. Обобщенная количественная характеристика признака в статистической совокупности в конкретных условиях места и времени – это: а) абсолютная величина; б) средняя величина; в) относительная величина. 5. Сумма относительных показателей координации, рассчитанная по одной совокупности, должна быть: а) строго равной 100; б) меньше 100 или равной 100; в) меньше, больше или равной 100. 6. По степени агрегированности моделей статистические показатели подразделяются на:
7. В зависимости от характера изучаемых явлений статистические показатели делятся на: а) объемные и качественные; б) индивидуальные и обобщающие; в) интервальные и моментные. 8. Статистический показатель – это: а) обобщающий показатель, дающий числовую меру соотношения между двумя величинами; б) количественная оценка социально-экономических явлений; в) совокупность статистических данных. 9. Показатель, характеризующий состав той или иной совокупности, – это: а) относительный показатель структуры; б) относительный показатель динамики; в) относительный показатель сравнения. 10. Показатель, представляющий собой соотношение одного и того же абсолютного показателя, характеризующего разные объекты (предприятия, фирмы, страны, и т. д.), – это: а) относительный показатель координации; б) относительный показатель уровня экономического развития; в) относительный показатель сравнения. Задачи Примеры решения задач Пример 1. Выпуск продукции предприятием в январе - апреле 2010 г. характеризуется следующими данными (табл. 3.1).
Таблица 3.1– Выпуск продукции ОАО «Автоснаб» в 2010 г.
Рассчитаем относительные показатели динамики с переменной и постоянной базой сравнения: Таблица 3.2 – Расчет относительных показателей динамики
Относительные показатели динамики с переменной и постоянной базой сравнения взаимосвязаны между собой: произведение всех относительных показателей с переменной базой равно относительному показателю с постоянной базой за исследуемый период. Так, например:
Пример 2. На начало мая 2010 г. численность граждан, состоящих на учете в службе занятости, составляла 1590 тыс. человек, а число заявленных предприятиями вакансий – 309 тыс. Отсюда следует, что на каждых 100 незанятых приходилось 19 свободных мест:
Задачи 1. Используя данные о цене подсолнечного масла на внутреннем и мировом рынках составляла (табл. 3.3.), проведите сравнительный анализ цен, отметьте виды использованных относительных величин по аналитической функции.
Таблица 3.3 – Цена подсолнечного масла на внутреннем и мировом рынках, дол. США за 1т
2. На торгах фондовой биржи зафиксированы следующие цены акций (табл. 3.4.). Таблица 3.4 – Рыночная и номинальная стоимость акций предприятий на торгах фондовой биржи
Проведите сравнительный анализ курса акций, укажите виды использованных относительных величин.
3. В таблице 3.5 представлены данные о потреблении топлива ТЭЦ.
Таблица 3.5 – Потребление топлива ТЭЦ в 2009 – 2010 гг.
Определите: 1) объемы потребленного топлива за каждый год; 2) структуру потребленного топлива. Сделайте выводы относительно структурных сдвигов.
4. По приведенным данным о производстве и потреблении первичных энергоносителей в различных странах (табл. 3.5) определите для каждой из них относительные величины, которые характеризовали бы: а) динамику потребления и производства энергоносителей; б) степень самообеспеченности стран энергоресурсами.
Таблица 3.6 – Производство и потребление первичных энергоносителей в различных странах в 2000 и в 2010 гг., млн. т усл. топл.
Сделайте выводы о динамике зависимости стран от импорта первичных энергоресурсов.
5. Имеются следующие данные о производстве бумаги в РФ (табл. 3.7.).
Таблица 3.7 – Производство бумаги в РФ в 2007 – 2010 гг.
Вычислите относительные показатели динамики с переменной и постоянной базой сравнения. Проверьте их взаимосвязь. Сделайте выводы.
6. Известна структура произведенных затрат металлургических комбинатов России (табл. 3.8).
Таблица 3.8 – Структура произведенных затрат металлургических комбинатов России в 2010 г.
Вычислите относительные показатели координации.
7. Имеются следующие данные об урожайности пшеницы в некоторых странах (ц/га):
Рассчитайте относительные показатели сравнения. Сделайте выводы.
8. Имеются следующие данные о внешнеторговом обороте России со странами дальнего зарубежья и СНГ (табл. 3.9).
Таблица 3.8 – Внешнеторговый оборот России со странами дальнего зарубежья, млрд. дол. США
Вычислите относительные показатели структуры и координации.
Глава 4. Средние величины Основные понятия Средний показатель – это показатель в форме средней величины, представляющий собой обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени. Средняя величина – это обобщающая мера варьирующего признака, которая характеризует ее уровень в расчете на единицу совокупности. Условиями применения средних величин являются наличие качественно однородной совокупности и достаточно большой объем выборки. Средняя величина считается наиболее ценной и универсальной формой выражения статистических показателей. Определить среднюю во многих случаях можно через исходное соотношение средней (ИСС) или ее логическую формулу:
В каждом конкретном случае для реализации исходного соотношения требуется одна из форм средней величины. В статистической практике используют несколько видов средних величин: средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя квадратическая и т.д. Каждая из указанных средних может приобретать две формы: простую и взвешенную. Если среднюю вычисляют по первичным (несгруппированным) данным, применяют простую форму, если по вторичным (сгруппированным) – взвешенную. Средняя арифметическая является наиболее распространенной средней. Средняя арифметическая простая применяется, когда значение вариантов встречается один раз:
где
Средняя арифметическая взвешенная применяется, когда отдельное значение признака повторяется неодинаковое количество раз, т.е. она используется в расчетах средней по сгруппированным данным или вариационным рядам:
где При расчете средней по интервальному вариационному ряду для выполнения необходимых вычислений переходят от интервалов к их серединам. Средняя арифметическая обладает некоторыми математическими свойствами, которые более полно раскрывают ее сущность и в ряде случаев используются при ее расчетах: 1. Произведение средней на сумму частот равно сумме произведений отдельных вариантов на соответствующие им частоты:
2. Сумма отклонений индивидуальных значений признака от средней арифметической равна нулю:
3. Если все осредняемые варианты уменьшить (увеличить) на постоянное число А, то средняя арифметическая уменьшится (увеличится) на ту же величину:
4. Если все варианты значений признака уменьшить (увеличить) в А раз, то средняя также уменьшится (увеличится) в А раз:
5. Если все веса уменьшить или увеличить в А раз, то средняя арифметическая от этого не изменится:
Когда статистическая информация не содержит частот по отдельным вариантам совокупности, а представлена как их произведение, применяется формула средней гармонической взвешенной:
где Когда объемы явлений, т.е. произведения (
Средняя геометрическая – это величина, используемая как средняя из отношений или в рядах распределения, представленных в виде геометрической прогрессии. Средняя геометрическая используется в расчетах среднегодовых темпов роста и для определения равноудаленной величины от минимального и максимального признака. Средняя геометрическая простая вычисляется по формуле:
Средняя геометрическая взвешенная равна:
В качестве статистических характеристик вариационных рядов распределения рассчитываются так называемые структурные средние – мода и медиана.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 1797; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.01 с.) |

 .
. .
. .
. , или 190,7 %.
, или 190,7 %. .
. .
. ,
,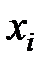 – i -й вариант усредняемого признака;
– i -й вариант усредняемого признака; – объем совокупности.
– объем совокупности. ,
, – вес i -го варианта.
– вес i -го варианта. .
.


 .
.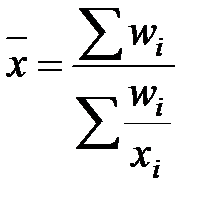 ,
,
 ), по каждому признаку равны, применяется средняя гармоническая простая:
), по каждому признаку равны, применяется средняя гармоническая простая: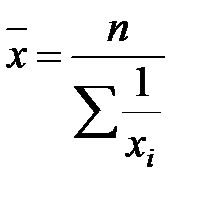 .
. .
. .
.


