
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 4. Группировка статистических данных.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Группировка - основной метод статистики. Виды статистических группировок. Принципы выбора группировочного признака. Образование групп и интервалов группировки. Статистические ряды распределения. Статистические таблицы, их виды и принципы построения. Графический метод представления статистических данных.
Вопрос 1. Группировка статистических данных является основой научной сводки и обработки данных. По своему содержанию статистическая сводка представляет собой совокупность приемов, позволяющих получить обобщенную характеристику изучаемого явления по ряду существенных для него признаков. Статистическая сводка включает следующие операции: 1. Группировку данных статистического наблюдения, т.е. составление рядов распределения 2. Суммирование (это сводка в узком понимании) показателей по отдельным группам и по всей совокупности, т.е. получение статистических показателей в абсолютной форме. 3. Расчет на основе абсолютный показателей статистических показателей в относительной форме. 4. Табличное или графическое оформление результатов сводки и их анализ. Таким образом, первым этапом проведения статистической сводки является группировка статистических данных наблюдения, поэтому группировка является решающим звеном статистической сводки. Она позволяет выявить и отграничить разнокачественные единицы наблюдения, входящие в совокупность и одновременно объединить в группы одно-качественные единицы наблюдения. Статистическая группировка представляет собой процесс образования однородных групп на основе расчленения статистической совокупности на части или объединение изучаемых единиц в частные совокупности по существенным для них признакам. Признаки, по которым производится распределение единиц наблюдаемой совокупности на группы, называют группировочными признаками или основанием группировки (например, совокупность предприятий можно прогруппировать по следующим признакам - объем товарооборота, численность работников и т.д.). Статистические группировки позволяют решить следующие задачи: 1. Выделить типы и существенно различные стороны, составляющие сложное общественное явление 2. Охарактеризовать выделенные типы и формы системой статистических показателей 3. Установить взаимосвязи между отдельными типическими группами 4. Определить характер взаимодействия между отдельными признаками совокупности в целом и по составляющим ее группам 4. Оценить влияние факторов на изменение результативного признака.
Вопрос 2. Исходя из задач, решаемых с помощью статистических группировок, в теории статистики выделяют следующие виды группировок: 1. Типологические группировки. Содержанием является выделение из множества признаков, характеризующих изучаемое явление, основных типов в качественно однородные. Типологические группировки широко применяются в экономических, социальных и др. исследованиях. Необходимость проведения типологической группировки обусловлена потребностью теоретического обобщенная первичной статистической информации и получения на этой основе обобщающих статистических показателей. При использовании метода типологических группировок важное значение имеет правильный выбор группировочного признака. 2. Структурные группировки. Выделенные типы явлений с помощью типологической группировки могут изучаться с точки зрения их структуры и состава. При этом используются структурные группировки, т.е. группировки применяемые для изучения строения совокупности. 3. Аналитические группировки - наиболее распространенный вид. Они применяются для выявления взаимосвязи между двумя или несколькими признаками общественных явлений (например, группировка предприятий по численности рабочих). Вопрос 3. Важнейшим вопросом теории группировок является выбор группировочных признаков, т. к. от выбора группировочного признака зависят результаты группировки, которые получают в процессе ее разработки. Статистика выделяет следующие основные правила выбора группировочных признаков: 1) при выборе группировочных признаков необходимо руководствоваться знанием сущности данного явления, законов его развития; 2) в основание группировки должно быть положено необходимое число наиболее существенных признаков, отвечающих задачам исследования; 3) группировочные признаки должны отбираться с учетом конкретных особенностей изучаемых явлений; 4) для всесторонней характеристики сложных общественных явлений целесообразно брать несколько группировочных признаков (два или более). Признаки, положенные в основу группировки, могут быть качественные (атрибутивные) или количественные (имеющие числовое выражение). При проведении группировок важное значение имеют правильное решение о том, на какое число групп следует подразделять совокупность. Если признак атрибутивный, то число групп, на которое следует подразделять совокупность, определяется числом качественных градаций этого признака. В случае, если группировочный признак количественного порядка, непрерывный или дискретный, с большим размахом вариации, то число групп может быть определено: 1. расчетным путем по формуле: n = 1+3,322 IgN, где n - число групп, N - численность совокупности; 2. по нормативам, а именно: если численность совокупности не превышает 25-30 единиц, то в расчет принимается 3-4 группы, 30-40 - 5-6; 40-60 - 6-8. При определении числа группировок необходимо их выбор производить таким образом, чтобы каждая группа была представительной, т. е. содержала не менее 7-10 единиц наблюдения, причем центральная часть интервала должна содержать не менее 50%. Для характеристики групп должны быть образованы интервалы, которые могут быть равные и неравные, открытые и закрытые. При равных интервалах их величина определяется по формуле: i = (Xmax – Xmin) / n = R / n; где n - число групп, R - размах вариации. При построении равных интервалов определяется нижняя и верхняя граница каждого из них, причем считается, что пределы наблюдения могут входить «включительно» или «исключительно». На практике применяются оба метода, но все же предпочтительнее принцип «исключительно».Например, группы работников магазина по производительности труда обозначены следующим образом: до 90 руб.; 90-120; 120-150; 150-180; свыше 180 руб. По принципу «включительно» к первой группе относится работник, производительность труда которого обозначается — до 90 руб.; по принципу «исключительно» этот работник включается во вторую группу—90—120 руб. Применение этих принципов зависит от формы написания интервалов, особенно первой и последней групп. В данном примере работника, производительность которого 180 руб., включают в предпоследнюю группу, поскольку ее интервал обозначен 150—180, а последний—свыше 180 руб. Соответственно работник, имеющий выработку 90 руб., Относится к первой группе. Если бы запись была «180 и более», то по принципу «исключительно» работник, имеющий выработку 180 руб., включался бы в последнюю группу. Открытые интервалы не имеют для 1-го интервала нижней границы, а для последнего – верхней. Неравные интервалы могут применяться при значительной вариации признака совокупности. Определяющим при этом является качественная однородность групп. Для характеристики установленных групп и их интервалов необходимо правильное определение показателей, которыми характеризуется каждая группа. При этом выбор показателей должен: 1) отразить общую картину развития экономического процесса; 2) проявить особенности каждого типа; 3) установить специфику проявления типа групп ли формы подгрупп применительно к различным регионам и зонам. Тщательный отбор показателей для анализа позволяет повысить результативность статистической группировки. Серединное значение интервалов определяется несколькими приемами: 1) Этот показатель можно рассчитать суммированием верхней и нижней границ интервала и делением суммы пополам. В нашем примере во втором интервале середина равна 105 руб. (90+120):2; в третьем - 135 руб.: (120+150): 2; в первом интервале - 75 руб. (60+90):2. Поскольку первый интервал является открытым (не имеет нижней границы), а имеющийся ряд распределения – интервальный, причем с равными интервалами (в 30 руб.), то предполагается, что нижней границей первого интервала будет является значение в 60руб. (90 – 30). 2) Эти значения также получают прибавлением к серединному значению второго интервала величины равного интервала (105+30). Вычитая величину равного интервала из серединного значения второго интервала, будем иметь середину первого (105—30), а середина последнего, открытого интервала определяется прибавлением длины интервала к середине интервала из предпоследней группы (165+30=195).
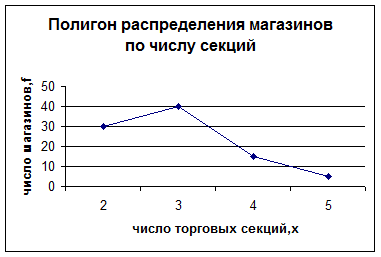
Вопрос 4. Результаты сводки и группировки материалов статистического наблюдения оформляются в виде статистических рядов распределения и таблиц. Статистические ряды распределения представляют собой упорядоченное расположение единиц изучаемой совокупности на группы по группировочному признаку. Они характеризуют состав (структуру) изучаемого явления, позволяют судить об однородности совокупности, границах ее изменения, закономерностях развития наблюдаемого объекта. Ряды распределения, образованные по качественным признакам, называют атрибутивными. Например, распределение работников торговли по занимаемой должности, профессии, образованию; распределение товарооборота по формам торговли, товарным группам; распределение работников по возрасту, стажу работы, производительности труда, заработной плате и другим признакам. При группировке ряда по количественному признаку получаются вариационные ряды. При этом вариационные ряды по способу построения бывают дискретными (прерывными), основанными на прерывной вариации признака (например, число касс в магазине, комнат в квартире), и интервальными (непрерывными), базирующимися на непрерывно изменяющемся значении признака, имеющими любые (в том числе и дробные) количественные выражения (объем товарооборота, величина фонда оплаты труда, выработка продавца). В практике применяются также и интервальные ряды распределения. При их построении возникают вопросы о числе групп, величине интервала, его границе. Вариационные ряды состоят из двух элементов: варианты и частоты. Варианта - это отдельное значение варьируемого признака, которое он принимает в ряду распределения. Частотами называются численности отдельных вариант или каждой группы вариационного ряда. Частоты, выраженные в долях единицы или в процентах к итогу, называются частостями. Сумма частот составляет объем ряда распределения. Каждый ряд распределения может быть представлен графически. Графическое изображение рядов распределения облегчает их анализ и позволяет судить о форме распределения наглядно. Для графического изображения дискретного ряда применяют полигон распределения. Для его построения на оси абсцисс откладывают значения признака, а на оси ординат - частоту. Например, в таблице представлен ряд распределения магазинов по числу торговых секций
Данный ряд распределения является дискретным, так как варианта (число секций) представлена здесь целым числом (2,3,4,5), и полигон распределения данного ряда будет иметь следующий вид:
Для графического изображения интервального вариационного ряда применяется гистограмма. При ее построении на оси абсцисс откладываются интервалы ряда, высота которых равна частотам, отложенным на оси ординат. Над осью абсцисс строятся прямоугольники, площадь которых соответствует величинам произведений интервалов на их частоты.
Графическое изображение (гистограмма) данного ряда распределения будет иметь следующий вид:
Число магазинов, f
2 4 6 8 группы магазинов по числу секций, х
В практике экономической работы возникает потребность в преобра- зовании рядов распределения в кумулятивные ряды, строящиеся по накопленным частотам. (с их помощью можно определить структурные средние, прослеживать за процессом концентрации изучаемого явления). Используя накопленные частоты строят график в виде кумуляты (кривой сумм). При графическом изображении кумуляты накопленные частоты наносят на поле графика в виде перпендикуляров к оси абсцисс в верхних границах интервалов. Длина этих линий равна величине накопленных частот в конкретном интервале. Соединяя затем эти перпендикуляры, получаем ломаную линию.
Графическое изображение (кумулята) данного ряда распределения, построенного по накопленным частотам, будет иметь следующий вид:
накопленная частота, f ‘
100 -
2 4 6 8 х, группы магазинов по числу секций
Если вариационный ряд распределения представлен в виде неравных интервалов, то для правильного представления о характере распределения необходимо рассчитать плотность распределения (абсолютную или относительную), т.е. определить сколько единиц в каждой группе приходится на единицу величины интервала. Абсолютная плотность:
Относительная плотность:
где f - частота w - частость (доля) i - величина интервала. При построении графика с неравными интервалами высоту прямоугольников определяют пропорционально не частотам, а показателям плотности распределения признака в интервалах.
Абсолютная плотность распределения, рабс
40 -
2 4 5 8 группы магазинов по числу секций, х
Вопрос 5. Статистической таблицей называется способ рационального и наглядного изложения и обобщения данных о социально-экономических явлениях при помощи цифр, расположенных в определенном порядке. В статистических таблицах в отличие от любых других таблиц всегда дается определенная характеристика той или иной области общественной жизни. Основное преимущество табличной формы изложения статистических данных заключается в том, что таблица позволяет производить наглядное сопоставление данных, облегчает и ускоряет восприятие информации, интенсифицирует познавательный процесс. По технике построения статистическая таблица представляет собой ряд взаимопересекающихся горизонтальных и вертикальных линий, образующих по горизонтали строки, а по вертикали графы. Принципиальная схема таблицы, т.е. составные части и элементы должны иметь: 1) название таблицы (общее заглавие), которое должно отражать содержание таблицы; 2) нумерация таблиц; 3) наименование граф, верхние заголовки, т, е. статистическое сказуемое; 4) наименование строк, боковые заголовки, т. е. статистическое подлежащее; 5) клетка 6) итоговая строка; 7) итоговая графа; 8) нумерация строк или граф. Нумерация подлежащего осуществляется буквами, а признаков - цифрами; цель - облегчение пользования таблицей и показателями для расчета. 9) примечание к таблице. Статистическая таблица представляет собойсвоеобразное статистическое предложение, поэтому в ней выделяется подлежащее и сказуемое. Подлежащим статистической таблицы называются те объекты или составные части, которые рассматриваются в данной таблице. Сказуемым называется то, что говорят о подлежащем, об изучаемом объекте, т. е. какие показатели приведены в таблице для его характеристики. Вид статистической таблицы определяется по виду подлежащего таблицы. Таблицы подразделяются на простые, групповые и комбинационные. Простой называется таблица, подлежащее которой содержит перечень единиц наблюдения. Групповой называется таблица, подлежащее которой содержит группировку единиц наблюдения по одному какому-либо существенному признаку, т. е. простая группировка Комбинационной называется такая таблица, подлежащее которой содержит группировку единиц изучаемой совокупности по двум и более существенным признакам, связанным между собой. Правила составления и приемы чтения (анализа) статистических таблиц. Для отражения достоверной характеристики изучаемого явления, процесса должны быть составлены рационально построенные статистические таблицы. Построение макета статистической таблицы определяется целью статистического исследования и конкретным содержанием обрабатываемого материала. Чтобы построить рациональную таблицу необходимо соблюдать следующие требования: 1) при разработке макета таблицы учесть размерность таблицы, ее компактность. Взамен одной громоздкой таблицы целесообразно создать 2-3 таблицы меньших размеров. 2) должна быть четкая, краткая и ясная формулировка наименований заголовка, строк подлежащего и граф сказуемого. При этом заголовок таблицы должен раскрывать ее содержание (в нем указывается также время, место события и единица измерения признака). 3) должна быть нумерация строк и граф, что облегчает пользование таблицей, а в ряде случаев служит для изложения техники вычисления показателей; 4) округление чисел с одинаковой степенью точности; 5) таблица должна содержать групповые и общие итоги по всем показателям, что облегчает пользование таблицей и дает возможность обнаружить ошибки в подсчетах.
Вопрос 6. Полученный в результате разработки статистический материал, часто нуждается в наглядном изображении с помощью построения статистических графиков. В статистике графиками называются наглядные изображения статистических величин в виде различных линий, геометрических фигур или географических картосхем. Главное достоинство графиков - их наглядность. При правильном построении графика статистические показатели привлекают к себе внимание, становятся выразительными, лаконичными и запоминающимися. Наряду с этим статистические графики имеют важное аналитическое значение. В статистическом графике различают следующие основные элементы: поле графика, графический образ, пространственные и масштабные ориентиры, экспликация графика. Полем графика является место, на котором он выполняется (листы бумаги, план местности и т.д.) Графический образ - это символические знаки, с помощью которых изображаются статистические данные (точки, линии и т.д.). Пространственные ориентиры определяют размещение графических образов на поле графика. Они задаются координатной сеткой или контурными линиями и делят поле графика на части, соответствующие значениям изучаемых показателей.. Масштабные ориентиры статистического графика придают графическим образам количественную значимость, которая передается с помощью системы масштабных шал. Масштаб графика - это мера перевода численной величины в графическую. Масштабной шкалой является линия, отдельные точки которой читаются (в соответствии с принятым масштабом) как определенные числа. Экспликация графика - это пояснение его содержания. Включает в себя заголовок графика, объяснения масштабных шкал, пояснения отдельных элементов графика. При всем своем многообразии статистические графики классифицируются по ряду признаков: 1) По способу построения статистические графики подразделяются на диаграммы, картограммы и картодиаграммы. Диаграмма представляет чертеж, на котором статистическая информация изображается посредством геометрических фигур или символических знаков. В сою очередь диаграммы бывают: а) линейными. Для их построения обычно принимается прямоугольная система координат. На оси абсцисс откладываются варианты изучаемого показателя (или показания времени), а по оси ординат - величина изучаемого показателя. По отметкам (точкам) обеих осей определяют положения каждого уровня на поле графика Последовательно соединяя точки отрезками линий, получают линию графика, так называемую статистическую кривую. ––––––– -общий объем товарооборота; – – – – – -товарооборот продовольственных товаров; –. –. –. – товарооборот непродовольственных товаров.
Рисунок 1 – объем товарооборота предприятия в 1995 – 1999 годах (в % к 1995 году).
б) столбиковыми. Здесь каждое значение изучаемого показателя изображается в виде вертикального столбика Основание столбика располагается на оси абсцисс, ширина столбиков произвольная, но для всех одинаковая, одинаковое расстояние между столбиками. Величины характеризующие значение изображаемых показателей, помещаются внутри каждого столбика..
Рисунок 2 – объем товарооборота предприятия. в) ленточными. В этих диаграммах основания столбиков располагаются вертикально, а масштабная шкала наносится на горизонтальную ось. Длина полос соответствует значениям изображаемых показателей.
Рисунок 3 – выполнение задания по объему товарооборота магазином за 1 квартал 1999года. г) круговыми. В этих диаграммах площадь окружности принимается за величину всей изучаемой статистической совокупности, а площади отдельных секторов отображают удельный вес (долю) ее составных частей..
Рисунок 4 – состав населения Орловской области в 1997 году.
Картограмма - это изображение величины интересующего нас признака на географической карте с помощью графических символов (штриховки, расцветки, точек). При этом штриховать надо тем гуще, чем больше размер показателя. Картодиаграмма представляет собой сочетание картограммы с диаграммой. На картодиаграммах распределение показателей по территории дается на схематической географической карте в форме столбиков, треугольников и других графических знаков. 2) В зависимости от формы применяемых графических образов графики могут быть точечными (в качестве графических образов применяется совокупность точек), линейными графическими образами являются линии), плоскостными (геометрические фигуры) и фигурными. 3) В зависимости от характера решаемых задач графики классифицируются по их целевому применению в статистическом изучении коммерческой деятельности на рынке товаров и услуг. Различают следующие основные виды графиков: рядов распределения, структуры статистической совокупности, рядов динамики, показателей связи, показателей выполнения заданий. Расмотренные виды графиков нельзя считать непрерывающие, правильнее сказать, что они наиболее часто употребляемы.
ТЕМА 5. СРЕДНИЕ ВЕЛИЧИНЫ. Назначение средних величин. Виды средних величин. Свойства средних величин. 4. Структурные средние величины (мода и медиана). Вопрос1. Характеристика признаков явлений или общих целей, общих закономерностей процесса, являющейся важнейшей социально-экономической задачей решается при помощи средних величин. Однако эта общая задача должна быть конкретизирована более частными задачами. В экономике можно выделить несколько основных вопросов, решение которых связано с вычислением средних величин: n характеристика уровня развития явления n сравнение двух или нескольких уровней n характеристика изменения уровня, явлений во времени n выявление и характеристика связей и закономерностей развития явления n производство расчетов и их оценка в связи с планированием, прогнозированием, балансовыми расчетами и т.д. С помощью средних величин проводится много аналитических исследований при решении народнохозяйственных задач в целом или по отраслям, когда приводятся важнейшие характеристики состояния и развития отрасли, предприятия и т.д. «Аналитическая сила» средних величин состоит в обобщении соответствующей совокупности типичных, однородных показателей, явлений, процессов. Они позволяют переходить от единичного к общему, от случайного к закономерному, сглаживая различая в величине признака, которые возникают по тем или иным причинам у отдельных единиц наблюдения. Вопрос 2. Средней величиной называется обобщающий показатель, характеризующий типичные размеры и количественное соотношение варьирующих признаков качественно однородной совокупности.
Различают следующие виды средних величин: n средняя арифметическая n средняя гармоническая n средняя геометрическая n средняя квадратическая n структурные средние - мода и медиана. В теории статистики различают следующие формы средних величин: n простая форма (не взвешенная) n сложная (взвешенная) или агрегатная форма. Основной исходной формой средних величин является степенная средняя, которая имеет следующий вид:
где Х - варианта признака, n - число единиц совокупности, к - показатель степени. Взвешенная степенная средняя имеет следующий вид: где f - частота повторения признака в совокупности. Придавая определенные значения к и преобразуя формулу средней можно получить следующие виды средних величин: при к = 1 - средняя арифметическая при к = 0 - средняя геометрическая при к = -1 средняя гармоническая при к = -2 - средняя квадратическая. Средняя арифметическая - наиболее распространенный вид средней, которая может быть выражена при помощи формул: 1. Простая средняя арифметическая исчисляется тогда, когда значения вариантов встречаются по одному или одинаковому числу раз, т.е. когда повторяемость каждого варианта одинакова
2. Взвешенная средняя арифметическая исчисляется тогда, когда отдельные значения признака повторяются неодинаковое число раз
где Х - варианта признака, n - число единиц в совокупности, f - частота.
В статистической практике бывают случаи, когда при вычислении средней имеются данные об индивидуальных значениях признака (Х) и его общем объеме в совокупности (w), но не известны частоты (f). В таких случаях среднее значение признака исчисляется по формуле средней гармонической, которая представляет собой величину, обратную средней арифметической из обратных значений вариант. 1. Простая средняя гармоническая имеет следующий вид:
2 Взвешенная средняя гармоническая выражается формулой:
Средняя геометрическая величина применяется при расчетах средних темпов роста для рядов динамики и имеет следующий вид:
где П (Х) – произведение, n - число лет
Средняя квадратическая величина применяется для оценки вариации признака от среднего уровня, при расчете среднего и квадратического отклонения и дисперсии, при расчете коэффициента вариации, при проверке правила сложения дисперсии, в дисперсионном анализе, при расчете моментов в рядах распределения, коэффициентов асимметрии и эксцесса и т.д. 1. Простая средняя квадратическая определяется по формуле:
2. Взвешенная средняя квадратическая:
Вопрос 3. Важнейшими свойствами средних величин являются следующие: 1. Произведение средней величины на сумму частот всегда равно сумме произведений вариантов и частот 2. Сумма отклонений вариант как от простой, так и от взвешенной средней всегда равна нулю:
3. Если все варианты уменьшить или увеличить на одно и тоже число а, то средняя величина уменьшится или увеличится на это же число а:
4. Если варианты признака уменьшить или увеличить в а раз, то средняя увеличится или уменьшится в это же число раз:
5. Если все частоты увеличить или уменьшить в какую-то величину d, то средняя от этого действия не изменится:
6. Если веса всех вариант признака равны между собой, то взвешенная средняя будет равна простой средней: Учитывая эти свойства, в статистике применяется расчет средней способом моментов ( для вариационного ряда с равными интервалами) по формуле:
где Х - срединное значение интервального вариационного ряда i - величина интервала f - частота повторения признака в совокупности А - условная величина. За условную величину А обычно принимается варианта, имеющая наибольшую частоту или доминирующее срединное положение в данном ряду. Эту формулу можно преобразовать следующим образом:
где средняя m1 из значений
Вопрос 4. Для характеристики структуры совокупности применяются особые показатели, которые можно назвать структурными средними. К таким показателям относятся мода и медиана. Модой или модальной величиной признака в ряду распределения является варианта, имеющая наибольшую частоту или частность. В дискретном ряду мода – это варианта с наибольшей частотой (например, пусть мы имеет ряд распределения женской кожаной обуви магазина:
В данном дискретном ряду модой будет являться 37-й размер обуви, так как он имеет наибольшую частоту покупки (60 раз)). В интервальном ряду мода определяется по формуле:
где Х0 - нижняя граница или минимальная граница модального интервала. Модальный интервал – это интервал, который имеет наибольшую частоту; i - величина модального интервала; f 1 - частота интервала, предшествующего модальному; f 2 - частота модального интервала; f 3 - частота интервала, следующего за модальным. Медиана – это срединное значение признака, которое делит ряд на равные части. Одна часть единиц варьирующего ряда имеет значение варьирующего признака меньше, чем медиана, другая часть - больше. Для дискретного ранжированного ряда (т. е. построенного в порядке возрастания или убывания индивидуальных величин) с нечетным числом членов медианой является варианта, расположенная в центре ряда. (Например, пусть мы имеем сведения о стаже работы 5 продавцов магазина: 1, 2, 5, 6, 9 лет. Данный ряд является ранжированным с нечетным числом членов (5 продавцов). Для данного ряда медиана будет равна 5 годам, так как ею в данном ряду является серединная, т.е. 3-я варианта со стажем работы 5 лет.) Для дискретного ранжированного ряда с четным числом членов медианой будет варианта рассчитанная из двух смежных центральных вариант. (Например, пусть мы имеет сведения о стаже работы 6 продавцов магазина: 1, 3, 4, 5, 7, 9 лет. Данный ряд является ранжированным с четным числом членов (6 продавцов). В этом ряду медиана будет рассчитываться как средняя арифметическая простая из двух смежных центральных вариант, которыми являются стаж работы 4 года и 5 лет. Тогда медиана для данного ряда будет равна (4+5)/2 =4,5 года, т. е. Для интервального вариационного ряда медиана будет определяться по формуле: | ||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

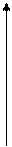


 20 -
20 -

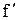




 -
- 50
50








 20 -
20 -
 Средняя величина (Х) представляет собой отношение абсолютного статистического показателя, который выражает общий объем явлений или признака, к численности совокупности этого явления. Индивидуальные значения признака называются вариантами этого признака и обозначаются Х, а число единиц совокупности, которые указываю на их повторение называются частотами (f) или весами (W).
Средняя величина (Х) представляет собой отношение абсолютного статистического показателя, который выражает общий объем явлений или признака, к численности совокупности этого явления. Индивидуальные значения признака называются вариантами этого признака и обозначаются Х, а число единиц совокупности, которые указываю на их повторение называются частотами (f) или весами (W). =
=  простая (не взвешенная)средняя степенная
простая (не взвешенная)средняя степенная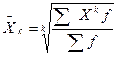




 где w - объем явления.
где w - объем явления.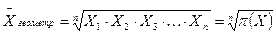


 .
.




 , если fi = f1.
, если fi = f1.

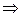
 ,
, - называется моментом первого порядка.
- называется моментом первого порядка. ,
, ).
).


