
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 7. Ряды динамики и их анализ.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Понятие о динамических рядах. Виды рядов динамики Показатели анализа ряда динамики Аналитическое выравнивание динамических рядов Основные методы прогнозирования рядов динамики Вопрос 1. Известно, что социально-экономические явления находятся в постоянном развитии во времени. Изучение процесса развития этих явлений - одна из основных задач статистики, которая решается путем построения и анализа рядов динамики. Динамика означает изменение процессов во времени, поэтому ряд статистических показателей, характеризующий изменение общественных явлений во времени называется динамическим рядом. Показатели, из которых состоит динамический ряд называются уровнями динамического ряда и обозначаются - У, а период времени, за который они представлены - t. В теории статистики различают следующие виды динамических рядов: 1. Моментные ряды динамики. Моментным называется ряд, уровни которого характеризуют размеры социально-экономических явлений по состоянию на определенную дату или определенный момент времени. 2. Периодические (интервальные) ряды динамики. Периодический ряд - это такой ряд, уровни которого характеризуют размеры общественно-экономических явлений за определенный период (интервал) времени. Ряды динамики формируются в результате сводки и обработки материалов периодического наблюдения. Повторяющиеся по временным периодам значения показателей в ходе статистической сводки систематизируются в хронологической последовательности. При этом каждый ряд динамики охватывает отдельные периоды, в которых могут происходить изменения, приводящие к несопоставимости отчетных данных с данными других периодов. Поэтому для анализа ряда динамики необходимо приведение всех составляющих его элементов к сопоставимому виду.
Вопрос 2. Для количественной оценки динамики социально-экономических явлений применяется система показателей ряда динамики, которая может быть представлена следующей группой показателей: 1. Абсолютный прирост 2. Темп роста 3. Темп прироста 4. Значение 1% прироста. В основе расчета показателей рядов динамики лежит сравнение его уровней. В зависимости от применяемого способа сопоставления (базисный или цепной) показатели динамики могут вычисляться на постоянной и переменной базах сравнения. Для расчета показателей на постоянной базе (базисный способ расчета) каждый уровень ряда сравнивается с одним и тем же базисным уровнем. Исчисляемые при этом показатели называются базисными. Для расчета показателей на переменной базе (цепной способ расчета) каждый последующий уровень ряда сравнивается с предыдущим. И показатели называются цепными. Важнейшим статистическим показателем является абсолютный прирост, который показывает абсолютную скорость роста или снижения сравниваемых уровней, и рассчитывается как разность между этими уровнями (между последующим и предыдущим уровнем, принятым за базу сравнения). Измеряется в тех же единицах, что и исходная информация. А = Y1 – Y0, где Y1 – значение отчетного уровня ряда динамики; Y0 – значение базисного уровня ряда динамики. Пусть мы имеем следующий ряд динамики производства продукции в 1990-1993 г.г.
На основании данного ряда динамики рассчитаем базисные (приняв за базу сравнения 1990 год) и цепные абсолютные приросты: Базисные: А91/90=Y91-Y90; А92/90= Y92-Y90; А93/90=Y93-Y90 Цепные: А91/90=Y91-Y90; А92/91= Y92-Y91; А93/92=Y93-Y92 Между цепными и базисными абсолютными приростами имеется следующая взаимосвязь: сумма цепных абсолютных приростов равна базисному абсолютному приросту последнего периода ряда динамики: А93/90=Y93-Y90=A91/90+A92/91+A93/92. Темп (коэффициент) роста показывает относительную скорость роста уровня ряда динамики и представляет собой отношение каждого последующего уровня к предыдущему, принятому за базу сравнения. Темп роста измеряется в %, а коэффициент роста - в долях.
Между цепными и базисными темпами роста имеется взаимосвязь: 1. Произведение последовательных цепных темпов роста равно базисному темпу роста последнего периода:
2. Частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста:
Темп (коэффициент) прироста показывает на сколько процентов изменился сравниваемый уровень с уровнем, принятым за базу сравнения:
Между темпом (коэффициентом) прироста и темпом (коэффициентом) роста существует следующая взаимосвязь: Тпр=Тр-100, Кпр=Кр-1. Значение 1 % прироста определяется отношением абсолютного прироста к темпу прироста, и показывает сколько единиц в абсолютном выражении приходится на 1% прироста для данного ряда динамики. Расчет этого показателя целесообразен для цепного способа, для базисного способа он не имеет смысла (будет постоянной величиной).
Расчет средних показателей ряда динамики. Для получения обобщающих показателей динамики социально-экономических явлений определяются средние величины ряда динамики: 1. Средний уровень ряда динамики характеризует типическую величину абсолютных уровней. В интервальных рядах динамики средний уровень определяется по формуле средней арифметической: - простой - взвешенной где Для моментного ряда средний уровень определяется с помощью средней хронологической:
2. Средний абсолютный прирост представляет собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики. При цепном способе для определения среднего абсолютного прироста сумма цепных абсолютных приростов делится на их число:
При базисном способе расчета чтобы определить средний абсолютный прирост, для этого определяется разность между конечным Уn и базисным У0 уровнями изучаемого периода, которая делится на m-1 субпериодов:
3. Средний темп роста - обобщающая характеристика индивидуальных темпов роста ряда динамики. Для определения среднего темпа роста цепным способом применяется следующая формула:
где Кр1, Кр2,..., Крn - индивидуальные (цепные) коэффициенты роста; n - число индивидуальных темпов роста Для базисного способа средний темп роста будет определяться по формуле:
4. Средний темп прироста можно определить по формуле:
5. Среднее значение 1 % прироста определяется только для цепного способа по формуле:
Эти показатели динамики находят практическое применение во всех расчетах, где требуется изучение изменения социально-экономических явлений во времени.
Вопрос 3. Важным направлением в исследовании закономерностей динамики социально-экономических процессов является изучение общей тенденции развития (тренда). На практике наиболее распространенными методами статистического изучения тренда являются: способ укрупнение интервалов (периодов), способ сглаживания скользящей средней, выравнивание ряда по среднегодовому абсолютному приросту, выравнивание ряда по среднегодовому темпу роста, аналитическое выравнивание при помощи способа наименьших квадратов. 1. Способ укрупнения интервалов применяется для выявления тренда в рядах динамики колеблющихся уровней, затушевывающих основную тенденцию развития. Сущность этого приема состоит в том, что данные или уровни за отдельные отрезки времени суммируются в ряды более продолжительных периодов (месячные в квартальные, квартальные в годовые), определяется средний уровень для полученного укрупненного периода. В результате после укрупнения периодов очевидной становится тенденция развития явления. 2. Способ скользящей средней. Скользящая средняя - это подвижная динамическая средняя, которая подсчитывается по динамическому ряду при последовательном передвижении на 1 год или на 1 интервал. Правильно исчисленная скользящая средняя устраняет в ряду динамики случайные колебания и дает возможность точнее выявить тенденцию в развитии, чем укрупненные интервалы. 3. Еще более точным способом является выравнивание по среднегодовому абсолютному приросту, которое рассчитывается по формуле:
где Y0 - начальный уровень ряда;
где n - число лет; t - порядковый номер года, в котором были приросты. 4. Выравнивание ряда по среднегодовому коэффициенту роста имеет следующий вид: где Y0 - начальный уровень ряда
n – число лет; t - порядковый номер года. 5. Способом аналитического выравнивания можно получить обобщенную статистическую оценку тренда. Наиболее совершенным является способ наименьших квадратов, которому соответствует условие, что сумма квадратов отклонений фактического и теоретического уровней будет минимальной. Простейшим приемом является выравнивание ряда динамики по прямой: где а - свободный член; b - коэффициент приращения; t - период времени. Способ наименьших квадратов дает систему двух нормальных уравнений для вычисления параметров функции:
где Y – исходные уровни ряда; n – число членов ряда; t – время. Для упрощения вычислений показателям времени t придают такие значения, чтобы их сумма была равна нулю ( - если ряд содержит четное число членов
- если ряд содержит нечетное число членов
где k – порядковый номер года; n – число лет в периоде. При
Исходя из полученной системы уравнений найдем параметры уравнения прямой:
ТЕМА 8. ИНДЕКСЫ.
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1208; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |

 ,
,  .
. ;
; .
. ,
,  .
. .
. ;
; ,
, - сумма уровней; n – число уровней.
- сумма уровней; n – число уровней. , где n – число уровней.
, где n – число уровней. .
. .
. *100,
*100, .
.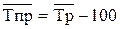 .
. .
. ,
,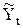 - выровненное значение;
- выровненное значение;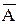 - средний базисный абсолютный прирост, который вычисляется по формуле:
- средний базисный абсолютный прирост, который вычисляется по формуле: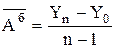 ,
, ,
, - среднегодовой базисный коэффициент роста, определяемый по формуле:
- среднегодовой базисный коэффициент роста, определяемый по формуле: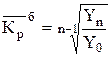 ,
,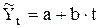 ,
,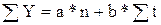 ,
,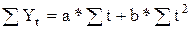 ,
, ). При этом используют следующие формулы:
). При этом используют следующие формулы:
 ,
,
 ,
, .
. ,
, .
.


