Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы выявления основной тенденции развития в рядах динамикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Основная тенденция развития (тренд) – этообщее направление в изменении уровней ряда: к росту, снижению или стабилизации с течением времени. Выявление основной тенденции развития называется в статистике также выравниванием ряда динамики. Применяются такие методы выравнивания, как метод укрупнения интервалов; метод скользящей средней (механическое сглаживание); метод аналитического выравнивания. Метод укрупнения интервалов заключается в том, что первоначальный ряд динамики преобразуется в новый ряд путем укрупнения периодов времени, к которым относятся уровни ряда динамики (одновременно уменьшается количество интервалов). Средние уровни, исчисленные по укрупненным интервалам, позволяют определить направление и характер (ускорение или замедление роста) основной тенденции развития. Метод скользящей средней заключается в том, что вычисляется средний уровень из определенного числа, обычно нечетного, первых по порядку уровней ряда, затем средний уровень из такого же числа уровней начиная со второго, затем – с третьего и т.д. То есть по уровням ряда рассчитываются скользящие средние путем последовательного сдвига на один период суммированных показателей. Полученный показатель относят к середине укрупненного периода. При определении числа уровней для расчета средней сначала берется наименьший период (например, 3-го или 4-го уровня), если тенденция не выявлена, то период укрупняется. Метод аналитического выравнивания – это наиболее эффективный способ выявления основной тенденции развития, позволяющий получить количественную модель развития данного ряда динамики. Аналитическое выравнивание предполагает то, что фактические уровни заменяются уровнями, вычисленными на основе определенной линии (прямой или кривой), выбранной в предположении, что она точнее всего отображает общую тенденцию явления. В основе метода лежит установление функциональной зависимости уровней ряда от времени Таблица 24 Виды трендовых моделей
Рассмотрим технику выравнивания ряда динамики по линейной функции. Выравненные уровни ряда динамики по этой функции вычисляются по следующему уравнению:
где
t – порядковый номер периода или момента времени. Параметры
где у – фактические (эмпирические) уровни ряда динамики; n – число уровней ряда. Поиск параметров уравнения можно значительно упростить, если ввести обозначения моментов или периодов времени так, чтобы их сумма была равна нулю. Так, если количество уровней ряда четное, то временные даты (t) обозначаются следующим образом: -3 -2 -1 +1 +2 +3. Если же количество уровней ряда нечетное, то обозначения устанавливаются так: -3 -2 -1 0 +1 +2 +3. В обоих случаях Σt = 0, так что система нормальных уравнений примет вид:
Откуда
Параметр На основе найденного уравнения рассчитывают теоретические уровни, соответствующие во времени фактическим уровням ряда ( Для оценки степени приближения выравненных уровней к фактическим данным рассчитывают среднее квадратическое отклонение тренда и коэффициент вариации по следующим формулам:
Если коэффициент вариации меньше 25%, то это свидетельствует о достаточном приближении теоретических уровней к фактическим.
Изучение сезонных колебаний в рядах динамики
Сезонные колебания – это сравнительно устойчивые внутригодичные колебания, т.е. когда из года в год в одни месяцы (или кварталы) уровень явления повышается, а в другие – снижается. Они обусловливаются специфическими условиями, влиянием многочисленных факторов, в том числе природно-климатических. Наличие сезонных колебаний выявляют с помощью графического метода. В этом случае применяют линейные диаграммы, на которые наносят данные об объеме явления по месяцам не менее чем за три года. Для измерения сезонных колебаний в статистике существует ряд методов. Один из них заключается в построении специальных показателей, которые называются индексами сезонности Is. Совокупность этих показателей образует сезонную волну. Для того чтобы выявить устойчивую сезонную волну, на которой не отражались бы случайные условия одного года, индексы сезонности вычисляют по данным за несколько лет (не менее трех), распределенным по месяцам. Расчет индексов сезонности выполняют двумя методами в зависимости от характера динамики. Если ряд динамики не содержит ярко выраженной тенденции в развитии, т.е. годовой уровень явления из года в год остается относительно неизменным, то индексы сезонности исчисляются непосредственно по фактическим данным без их предварительного выравнивания по приведенной ниже формуле:
где
Если уровни ряда динамики имеют тенденцию к развитию (от года к году повышаются или снижаются), то индексы сезонности определяются отношением фактических данных с выравненными по аналитическому выравниванию. Расчет индексов производится по формуле:
где
Общим показателем силы колебания ряда динамики сезонности за год является среднее квадратическое отклонение индексов сезонности, выраженное в процентах:
Чем меньше величина этого показателя, тем меньшей является сезонность исследуемого явления.
Задания для практических занятий и самостоятельной работы Задание 1. Имеются следующие данные об общем объеме розничного товарооборота региона по месяцам отчетного года, млн руб.:
Определите: 1) вид ряда динамики; 2) цепные и базисные показатели динамики товарооборота; 3) в целом за весь период средние показатели динамики. Сделайте соответствующие выводы. Результаты расчетов оформите в виде таблицы:
Задание 2. Имеются данные о товарных запасах в розничной сети торгующих организаций города в отчетном году, млн руб.:
Определите: 1) вид ряда динамики; 2) средние остатки товарных запасов за первое полугодие; за второе полугодие; за год.
Задание 3. За март отчетного года произошли следующие изменения в списочном составе работников организации, чел.:
Определите среднюю списочную численность работников организации в марте. Для расчетов используйте вспомогательную таблицу:
Задание 4. Имеются следующие данные о производстве продукции организации за 2000-2008 гг. (в сопоставимых ценах):
Выявите основную тенденцию производства продукции: 1) методом укрупнения интервалов; 2) методом скользящей средней; 3) методом аналитического выравнивания по линейной функции.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1613; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.234.182 (0.009 с.) |

 . При этом на практике чаще всего применяются следующие функции (табл. 24):
. При этом на практике чаще всего применяются следующие функции (табл. 24):


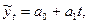 ,
, – теоретические (выравненные) уровни ряда;
– теоретические (выравненные) уровни ряда;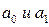 – параметры прямой;
– параметры прямой;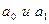 находятся по методу наименьших квадратов с помощью решения системы нормальных уравнений:
находятся по методу наименьших квадратов с помощью решения системы нормальных уравнений:



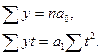

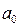 характеризует средний уровень ряда динамики,
характеризует средний уровень ряда динамики,  – средний абсолютный прирост, который показывает направление и характер основной тенденции развития.
– средний абсолютный прирост, который показывает направление и характер основной тенденции развития. ). По окончании расчетов целесообразно построить график, на котором следует изобразить исходные фактические данные и теоретические значения уровней ряда, характеризующие тенденцию ряда динамики.
). По окончании расчетов целесообразно построить график, на котором следует изобразить исходные фактические данные и теоретические значения уровней ряда, характеризующие тенденцию ряда динамики.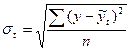 ;
;
 ,
,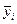 – средний уровень для каждого месяца;
– средний уровень для каждого месяца;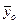 – среднемесячный уровень для всего ряда.
– среднемесячный уровень для всего ряда. ,
, – среднемесячный уровень выравненных данных для всего ряда.
– среднемесячный уровень выравненных данных для всего ряда.