Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обозначения, используемые в формулах средних величинСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Формулы расчета степенных средних величин показаны в таблице 12. Таблица 12 Формулы расчета степенных средних величин
Структурные средние величиныпредставлены на рисунке 15.
Рис. 15. Характеристика структурных средних величин
Порядок определения моды представлен на рисунке 16.
Рис. 16. Порядок определения моды
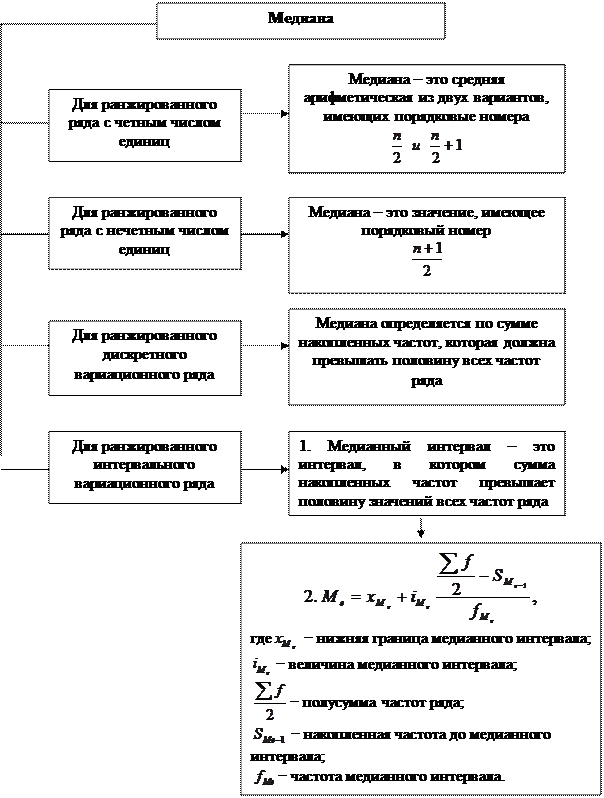
Порядок определения медианы представлен на рисунке 17.
Рис. 17. Порядок определения медианы Задания для практических занятий и самостоятельной работы
Задание 1. Имеются следующие данные о показателях работы предприятий отрасли за отчетный период:
Определите средние уровни каждого показателя по предприятиям отрасли.
Задание 2. Имеются следующие данные о продаже картофеля на рынках города:
Определите для каждого года средние цены картофеля по трем рынкам города вместе. Задание 3. Три работника в течение смены заняты изготовлением одинаковых деталей. Первый затрачивает на выработку одной детали 15 мин., второй – 20, третий – 18 мин. Определите среднее значение затрат времени на изготовление одной детали с помощью средней гармонической простой.
Задание 4. Имеются данные о финансовых показателях нескольких фирм за два периода:
Определите для каждого периода среднюю прибыль на одну акцию по трем фирмам вместе.
Задание 5. Продажа автомобилей на товарной бирже города характеризуется следующими данными:
Определите, как изменилась средняя цена одного автомобиля в апреле по сравнению с мартом с помощью относительной величины динамики. Задание 6. По следующим данным рассчитайте средний стаж работы рабочих предприятия:
Задание 7. Имеются следующие данные об оплате труда работников двух предприятий:
Определите среднемесячную заработную плату работников двух предприятий вместе, используя показатели: а) гр. 2 и 3; б) гр. 1 и 3; в) гр. 3 и 4.
Задание 8. Имеются следующие данные о цене товара по шести магазинам города на 1 января отчетного года:
Определите моду и медиану цены товара. Задание 9. Распределение магазинов по размеру товарооборота за октябрь отчетного года характеризуется следующими данными:
Определите моду и медиану размера товарооборота.
Задание 10. Имеются данные о сроках функционирования коммерческих банков на начало года:
Определите: 1) средний срок функционирования банков; 2) моду функционирования банков; 3) медиану функционирования банков. Задание 11. Определите моду и медиану в следующем ряду:
12 14 18 10 12 19 11 12 14 12 18 20.
Вопросы для самоконтроля
1. Какое значение имеет средняя величина в статистике? 2. Какие виды средних величин применяются в статистике? 3. По каким данным определяются простая и взвешенная средняя величина? 4. Какие средние величины используются в рядах распределения? 5.3. Показатели вариации и дисперсионный анализ
Вариация – это различие значений признака у разных единиц совокупности и их колебания около средней величины в один и тот же период или момент времени. Вариация присуща массовым явлениям. Она возникает в результате того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов, которые по-разному сочетаются в каждом конкретном случае. Для измерения вариации используются абсолютные и относительные показатели,формулы расчета которых представлены в таблице 13. Таблица 13 Показатели вариации
Примечание. Чем меньше значения показателей вариации, тем ниже вариация изучаемого признака и, следовательно, выше однородность совокупности и типичнее средняя.Совокупность считается количественно однородной, если коэффициент вариации не превышает 33%.
Для статистической совокупности, сгруппированной по изучаемому признаку, возможно исчисление трех видов дисперсий: общей, межгрупповой и средней внутригрупповой (табл. 14). Таблица 14 Дисперсионный анализ
Указанные дисперсии взаимосвязаны между собой следующим равенством: величина общей дисперсии равна сумме межгрупповой дисперсии и средней внутригрупповой дисперсии: Пользуясь правилом сложения дисперсий, можно по двум известным дисперсиям найти третью – неизвестную, а также иметь представление о силе влияния группировочного признака, вычислив коэффициент детерминации и эмпирическое корреляционное отношение. Коэффициент детерминации Эмпирическое корреляционное отношение
Задания для практических занятий и самостоятельной работы
Задание 1. Имеются следующие данные об остатках товаров в шести магазинах одной сети:
Определите на каждую дату показатели вариации остатка товаров: 1) размах вариации; 2) среднее линейное отклонение; 3) линейный коэффициент вариации. Сделайте вывод, на какую дату остаток товаров более устойчив.
Задание 2. Имеются следующие данные о распределении продовольственных магазинов региона по размеру товарооборота за месяц:
Определите: 1) средний размер товарооборота; 2) среднее линейное отклонение; 3) дисперсию; 4) среднее квадратическое отклонение; 5) коэффициент вариации товарооборота. Для расчетов рекомендуется использовать следующую таблицу:
Задание 3. По данным распределения работников предприятия по стажу определите показатели вариации (среднее квадратическое отклонение и коэффициент вариации):
Задание 4. Имеются следующие данные о результатах обследования рабочих предприятия по размеру месячной заработной платы. Общая дисперсия заработной платы в обследованной совокупности рабочих составила 450.
Определите, в какой степени вариация заработной платы рабочих предприятия зависит от возраста, рассчитав коэффициент детерминации и эмпирическое корреляционное отношение.
Задание 5. Имеются данные о чистой прибыли предприятий двух районов:
Определите дисперсии чистой прибыли: 1) внутригрупповые (по каждому району); 2) среднюю внутригрупповую; 3) межгрупповую; 4) общую; 5) коэффициент детерминации; 6) эмпирическое корреляционное отношение. Сделайте выводы.
Вопросы для самоконтроля
1. Что представляет собой вариация признака и от чего зависят ее размеры? 2. Какие показатели вариации вы знаете? 3. Что показывает коэффициент вариации? 4. Что представляет собой правило сложения дисперсий и в чем его практическое значение? 5. Какие показатели можно использовать для определения степени влияния факторного признака на результативный?
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 808; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.149.167 (0.011 с.) |




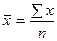









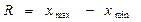



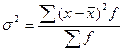
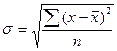








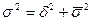 .
. показывает долю общей вариации результативного признака, обусловленную вариацией группировочного признака.
показывает долю общей вариации результативного признака, обусловленную вариацией группировочного признака. показывает тесноту связи между группировочным и результативным признаками (шкала Чеддока):
показывает тесноту связи между группировочным и результативным признаками (шкала Чеддока):