Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовые характеристики случайных величин.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Закон распределения случайных величин, представленный в той или иной форме, дает исчерпывающее описание случайной величины. Наиболее существенные особенности распределения в компактной форме описываются так называемыми числовыми характеристиками случайных величин. Они играют в теории вероятности огромную роль, с их помощью облегчается решение вероятностных задач. Рассмотрим наиболее часто встречающиеся числовые характеристики.
Характеристики положения.
Мат. Ожидание Мода Медиана
Важнейшая характеристика математическое ожидание, которая показывает среднее значение случайной величины. Математическое ожидание величины Х обозначается М[X], или mx. Для дискретных случайных величин математическое ожидание:
Сумма значений соответствующего значения на вероятность случайных величин.
Модой (Mod) случайной величины Х называют ее наиболее вероятное значение. Для дискретной случайной величины. Для непрерывной случайной величины.
Mod=X3 Mod=X0 Одно-модальное распределение
Много модальное распределение В общем случае Mod и математическое ожидание не совпадают.
Медианой (Med) случайной величины Х называют такое значение, для которой вероятность того что P(X<Med)=P(X>Med). У любого распределения Med может быть только один.
Med разделяет площадь под кривой на 2 равные части. В случае одно-модального и симметричного распределения mx=Mod=Med
Моменты. Чаще всего на практике применяются моменты двух видов начальное и центральное. Начальный момент.
Для непрерывной случайной величины Х начальным моментом Пользуясь знаком (оператором) М, начальный момент
Центрированной случайной величиной соответственной случайной величины Х называют отклонение случайной величины Х от ее математического ожидания:
Для дискретных случайных величин имеем:
Моменты центрированной случайной величины носят название Центральных моментов
Центральный момент порядка
Для дискретных случайных величин:
Для непрерывных случайных величин:
Связь между центральными и начальными моментами различных порядков
Из всех моментов в качестве характеристики случайной величины чаще всего применяют первый момент (мат. ожидание)
Второй центральный момент называют дисперсией случайной величины. Он имеет обозначение:
Согласно определению Для дискретной случайной величины: Для непрерывной случайной величины: Дисперсия случайной величины есть характеристика рассеянности (разбросанности) случайных величин Х около ее математического ожидания. Дисперсия означает рассеивание. Дисперсия имеет размерность квадрата случайной величины. Для наглядной характеристики рассеивания удобнее использовать величину, my той, что и размерность случайной величины. С этой целью из дисперсии извлекают корень и получают величину, называемую - среднеквадратичным отклонением (СКО) случайной величины Х, при этом вводят обозначение:
Среднеквадратичное отклонение иногда называют "стандартом" случайной величины Х. Итак:
Математическое ожидание mx и Dx (или СКО
Вернуться к вопросам
Вернуться к вопросам
Равномерное распределение Равномерная плотность распределения определяется следующим образом:

Функция распределения определяется:
Найдем числовые характеристики:
Вернуться к вопросам
Закон распределения Пуасона Рассмотрим дискретную случайную величину х, имеющую ряд распределения:
(k=m-1)
Вернуться к вопросам
Нормальный закон распределения (закон Гауса) Главная особенность в том, что он является предельным законом, к которому приближаются другие распределения, при весьма часто встречающихся типичных условиях. Нормальный закон распределения характеризуется плотностью вероятности вида:
Можно показать, что дисперсия
Вернуться к вопросам
Вернуться к вопросам
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 936; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.94.174 (0.009 с.) |




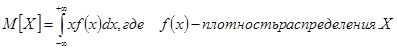





 -го порядка дискретной случайной величины Х называется сумма вида:
-го порядка дискретной случайной величины Х называется сумма вида:
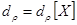
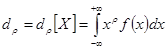 , очевидно, что математическое ожидание случайной величины есть первый начальный момент.
, очевидно, что математическое ожидание случайной величины есть первый начальный момент. 

 Математическое ожидание центрированной случайной величины равно 0.
Математическое ожидание центрированной случайной величины равно 0.






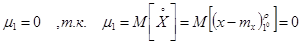
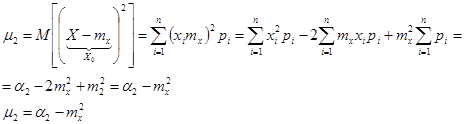
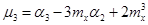
 и второй центральный момент
и второй центральный момент  .
.
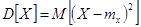




 ) наиболее частые употребляемые характеристики случайных величин, так как они определяют наиболее важные черты распределения, его положения и степень разбросанности.
) наиболее частые употребляемые характеристики случайных величин, так как они определяют наиболее важные черты распределения, его положения и степень разбросанности.







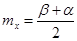 (математическое ожидание)
(математическое ожидание)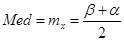 (медиана), Mod - не существует для данного распределения
(медиана), Mod - не существует для данного распределения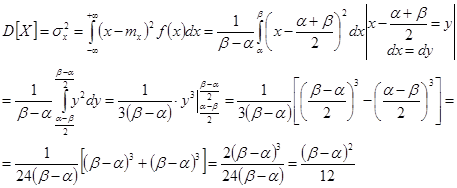
 (дисперсия),
(дисперсия),  (среднеквадратичное отклонение)
(среднеквадратичное отклонение) Говорят, что данное случайное распределение подчинено закону распределения Пуасона.
Говорят, что данное случайное распределение подчинено закону распределения Пуасона.