
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема о числовых характеристикахСодержание книги
Поиск на нашем сайте
I. Если c не случайная (детерминированная) величина, то M[c]=c и D[c]=0
II. Если c не случайная - постоянная, а Х случайная (детерминированная), то:
III. Математическое ожидание суммы нескольких величин равно сумме их ожиданий.
IV. Математическое ожидание линейной функции равно той же линейной функции от математических ожиданий аргументов.
V. Дисперсия суммы двух случайных величин равна сумме их дисперсий плюс удвоенный их корреляционный момент.
В общем случае:
Для не корреляционных случайных величин:
Вернуться к вопросам
В широком смысле слова, закон больших чисел характеризует устойчивость средних. При очень большом числе случайных явлений - перестает быть случайным и может быть предсказан с большей степенью определенности. В узком смысле под законом больших чисел понимается ряд математических теорем, в которых устанавливаются факты приближения средних характеристик большого числа опытов к некоторым определенным постоянным. Другая группа предельных теорем касается уже не предельных значений случайных величин, а предельных законов распределения. Эта группа теорем известна под названием " центральной предельной теоремы ". Неравенство Чебышева. P(|X-mx| > E) <= Dx/E2
Теорема Чебышева Теорема Чебышева дает одну из наиболее возможных форм закона больших чисел. Она устанавливает связь между средним арифметическим и ее математическим ожиданием наблюденных значений случайной величины. Yn=(X1 + X2 + …. + Xn) * 1/n = 1/n M[Yn] = i/n
Мат ожидание среднего не зависит от n
Теорема Чебышева устанавливает в точной количественной форме это свойство устойчивости среднего арифметического. Теорема Чебышева: При достаточно большом числе независимых опытов среднее арифметическое наблюденных значений случайной величины сходится по вероятности n т ее математическому ожиданию. В можематической форме это означает следующее:
Теорема Бернулли Теорема Бернулли: При неограниченном увеличении числа опытов n, частота события a сходится по вероятности к его вероятности P
Вернуться к вопросам
Центральная предельная теорема Рассмотрим одну из наиболее общих форм центральной предельной теоремы: Пусть имеется взвешенная сумма независимых случайных непрерывных величин x1, x2, x3, …., xn с произвольными законами распределения:
Пусть i-ая случайная величина имеет Согласно теореме о числовых характеристиках случайных величин, получим:
Центральная предельная теорема утверждает, что при достаточно общих условиях распределения суммарной Yn при
Опыт показывает, что когда Вернуться к вопросам
Вернуться к вопросам
Вернуться к вопросам
Доверительный интервал и доверительная вероятность используется в математической статистике точности и надежности полученной оценки a* неизвестного параметра a.
Найдем значение интервала 1. 2. вероятность, что выйдет за пределы интервала:
Интервал, Вероятность
Оценка a* называется точечной оценкой. Оценка Вернуться к вопросам
Рассмотрим серию из n однородных, не зависимых опытов, проводимых в одинаковых условиях, в каждом из которых может появиться или не появиться событие А. Вероятность появления F=P, не появления q=1-P. Предполагается, что вероятность р остается одной и той же в каждом опыте. Требуется найти вероятность Рm,n того, что А в этих n опытах появится ровно m раз (0<=m<=n).
Если производится n неизвестных опытов в каждом из которых событие А появляется с вероятностью Р, то вероятность того что событие А появится ровно m раз выражается формулой:
Вернуться к билетам.
Задача на схему случаев В урне 3 белых и 4 черных шара. Какова вероятность изъятия из урны трех черных шаров?
n - общее число возможных случаев изъятия 3 шаров из урны. m - число благоприятных случаев. (все три шара черные)
Вернуться к билетам.
|
|||||||||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 473; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.01 с.) |

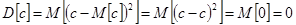
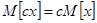
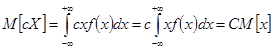
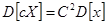
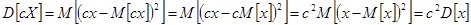
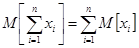
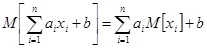
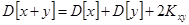
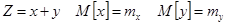
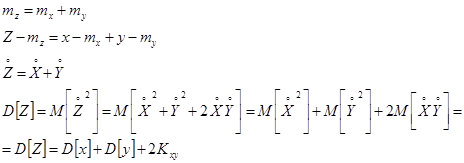
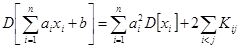 , где
, где 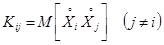
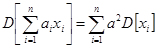
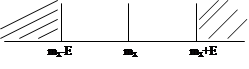
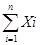
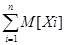 = 1/n *
= 1/n *  = 1/n * n * mx = mx
= 1/n * n * mx = mx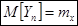
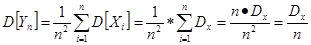
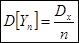
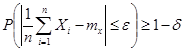 , где
, где 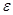 и
и 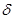 сколь угодно положительные числа
сколь угодно положительные числа 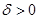 и
и 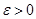 .
.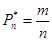 - (вероятность). m-произошло событие. n-число опытов.
- (вероятность). m-произошло событие. n-число опытов.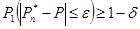
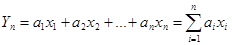 , где
, где 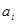 постоянная, фиксированная числа.
постоянная, фиксированная числа.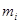 и
и 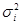 (i=1,2,3,…,n-1,n)
(i=1,2,3,…,n-1,n)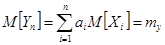
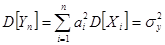
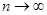 стремиться к нормальному распределению
стремиться к нормальному распределению 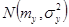
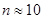 или меньше, то закон распределения суммы может быть заменен нормальным.
или меньше, то закон распределения суммы может быть заменен нормальным.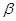 =0,95 или 0,98; 0,99 - Назначим вероятность достаточно большую.
=0,95 или 0,98; 0,99 - Назначим вероятность достаточно большую.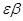 , при котором вероятность a*-a
, при котором вероятность a*-a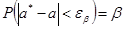
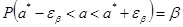

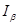 покрывающий a называется доверительным интервалом.
покрывающий a называется доверительным интервалом.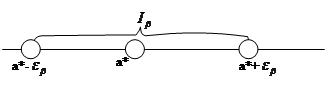
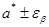 называется интервальной оценкой.
называется интервальной оценкой.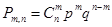 -Биномиальное распределение.
-Биномиальное распределение. 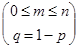
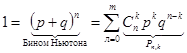 , где
, где 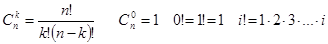
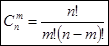
 ,
, 



