
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сумма событий и произведение событий.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Ответ на билет 1
X – случайная величина. x – значение случайной величины.
Дискретная случайная величина – можно пересчитать. Практически не возможное событие, вероятность которого близка к нулю 0 (0,01; 0,1). Практически достоверное событие, вероятность которого близка к единице 1 (0,99; 0,9888).
Вернуться к вопросам Ответ на билет 2 Сумма событий и произведение событий. А,В,….,G - события Суммой событий называется некоторое событие S=A+B+….+G=A Пример: Допустим идет стрельба по мишени А1 - попадание при первом выстреле А2 - попадание при втором выстреле S=A1+A2 (хотя бы одно попадание)
Произведением некоторых событий называется событие, состоящее в совместном появлении всех этих событий. S=ABC…G= Пример: А1 - промах при первом выстреле А2 - промах при втором выстреле А3 - промах при третьем выстреле
Теорема сложения вероятностей. Вероятность двух не совместных событий равна сумме вероятностей этих событий. P(A) P(B) P(A+B)=P(A)+P(B) S=S1+S2+…+Sn P(S)=P(S1)+P(S2)+…+P(Sn) Следствие: Если событие S1, S2, …, Sn образуют полную группу не совместных событий, то сумма их вероятностей равна 1.
Противоположными событиями называются два не совместных события, образующие полную группу .
Если два события A и B совместны, то вероятность совместного появления двух событий вычисляется по формуле: Условие независимости события А от события В: P(A|B)=P(A), то P(B|A)=P(B) Условие зависимости события А от события В: P(A|B) Вероятность произведения двух событий равна произведению вероятности одного из событий на условную вероятность другого, вычисленную при условии, что событие первое имело место: P(AB)=P(A)P(B|A), P(AB)=P(B)P(A|B) Следствие: Вероятность произведения нескольких не зависимых событий равна произведению вероятностей этих событий. P(A1A2…An)=P(A1)P(A2)…P(An) Пример: на монете выпадет орел 2 раза S=AорAор S=P2(A)=(1/2)2=1/4
Вернуться к вопросам
Закон распределения случайных величин Ряд и многоугольник распределений. Случайная величина - это величина, которая в результате опыта может принять то или иное значение не известное заранее какое. Большие буквы - случайные величины. Малые буквы - их возможные решения. Рассмотрим случайную дискретную величину Х с возможными значениями x1, x2, …, xn В результате опыта: Обозначим вероятность соответствующих событий через Pi
Х полностью описана с вероятностной точки зрения, если мы зададим распределение вероятности pi(i=1,2…,n), то есть в точности указаны решения вероятности pi каждого события xi Этим будет установлен закон случайной величины xi. Законом распределения случайной величины называется всякое соотношение устанавливающее связь между возможными значениями случайных величин и соответствующими вероятностями. Простейшей формой записи законов распределения является таблица:
Многоугольник и ряд распределения полностью характеризует случайную величину и является одной из форм законов распределения. (Для непрерывной случайной величины построить невозможно).
Вернуться к вопросам
Плотность и функция распределения. Функция распределения непрерывной случайной величины (Х), задана выражением:
a) Найти коэффициент а b) Найти плотность распределения F(x) c) Найти вероятность попадания случайной величины на участок P(0,5<x<3)=? d) Построить график функций
F(4)=1 -> a4=1, a=0,25
        
Вернуться к вопросам
Функция распределения Для непрерывной случайной величины Х вместо вероятности равенства Х=х используют вероятность Р(Х<х). F(x)=P(X<x) F-функция распределения случайной величины х F(x) -интегральный закон распределения или интегральная функция распределения. F(x) -самая универсальная характеристика случайной величины, она существует для всех случайных величин как дискретных так и непрерывных. Формула полной вероятности. Пусть требуется определить вероятность некоторого события А, которое может произойти вместе с одним из событий H1, H2, …, Hn, образующие полную группу не совместных событий. Эти события назовем гипотезами. Докажем, что в этом случае вероятность событий:
Вероятность события А вычисляется как сумма произведений вероятностей каждой гипотезы на условную вероятность события при этой гипотезе.
Теорема гипотез (формула Байеса). Пусть вероятность полной группы не совместных гипотез H1, H2, …, Hn известны и равны P(H1), P(H2), …, P(Hn). Событие А может появиться совместно с условной вероятностью P(A|Hi) (i=1,2,…,n). Спрашивается, как следует изменить вероятности гипотез после проведения опытов в связи с появлением этого события. Иными словами, требуется найти условную вероятность P(Hi,A).
Формула Байеса:
Вернуться к вопросам
Характеристики положения.
Мат. Ожидание Мода Медиана
Важнейшая характеристика математическое ожидание, которая показывает среднее значение случайной величины. Математическое ожидание величины Х обозначается М[X], или mx. Для дискретных случайных величин математическое ожидание:
Сумма значений соответствующего значения на вероятность случайных величин.
Модой (Mod) случайной величины Х называют ее наиболее вероятное значение. Для дискретной случайной величины. Для непрерывной случайной величины.
Mod=X3 Mod=X0 Одно-модальное распределение
Много модальное распределение В общем случае Mod и математическое ожидание не совпадают.
Медианой (Med) случайной величины Х называют такое значение, для которой вероятность того что P(X<Med)=P(X>Med). У любого распределения Med может быть только один.
Med разделяет площадь под кривой на 2 равные части. В случае одно-модального и симметричного распределения mx=Mod=Med
Моменты. Чаще всего на практике применяются моменты двух видов начальное и центральное. Начальный момент.
Для непрерывной случайной величины Х начальным моментом Пользуясь знаком (оператором) М, начальный момент
Центрированной случайной величиной соответственной случайной величины Х называют отклонение случайной величины Х от ее математического ожидания:
Для дискретных случайных величин имеем:
Моменты центрированной случайной величины носят название Центральных моментов
Центральный момент порядка
Для дискретных случайных величин:
Для непрерывных случайных величин:
Равномерное распределение Равномерная плотность распределения определяется следующим образом:

Функция распределения определяется:
Найдем числовые характеристики:
Вернуться к вопросам
Закон распределения Пуасона Рассмотрим дискретную случайную величину х, имеющую ряд распределения:
(k=m-1)
Вернуться к вопросам
Нормальный закон распределения (закон Гауса) Главная особенность в том, что он является предельным законом, к которому приближаются другие распределения, при весьма часто встречающихся типичных условиях. Нормальный закон распределения характеризуется плотностью вероятности вида:
Можно показать, что дисперсия
Вернуться к вопросам
Вернуться к вопросам
Задача на схему случаев В урне 3 белых и 4 черных шара. Какова вероятность изъятия из урны трех черных шаров?
n - общее число возможных случаев изъятия 3 шаров из урны. m - число благоприятных случаев. (все три шара черные)
Вернуться к билетам.
Ответ на билет 1
X – случайная величина. x – значение случайной величины.
Дискретная случайная величина – можно пересчитать. Практически не возможное событие, вероятность которого близка к нулю 0 (0,01; 0,1). Практически достоверное событие, вероятность которого близка к единице 1 (0,99; 0,9888).
Вернуться к вопросам Ответ на билет 2 Сумма событий и произведение событий. А,В,….,G - события Суммой событий называется некоторое событие S=A+B+….+G=A Пример: Допустим идет стрельба по мишени А1 - попадание при первом выстреле А2 - попадание при втором выстреле S=A1+A2 (хотя бы одно попадание)
Произведением некоторых событий называется событие, состоящее в совместном появлении всех этих событий. S=ABC…G= Пример: А1 - промах при первом выстреле А2 - промах при втором выстреле А3 - промах при третьем выстреле
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 827; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.007 с.) |


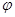 - непрерывная случайная величина
- непрерывная случайная величина B
B 
 (не одного попадания)
(не одного попадания)
 (пример - монетка имеющая орел и орешко)
(пример - монетка имеющая орел и орешко)

 P(A), P(B|A)
P(A), P(B|A) 
 , так как рассматриваемые события образуют полную группу не совместных событий, то
, так как рассматриваемые события образуют полную группу не совместных событий, то 





 - два способа решения.
- два способа решения.

 применяем 2 е теоремы:
применяем 2 е теоремы:
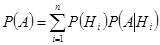 -формула полной вероятности
-формула полной вероятности




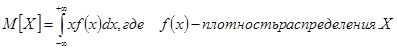





 -го порядка дискретной случайной величины Х называется сумма вида:
-го порядка дискретной случайной величины Х называется сумма вида:
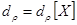
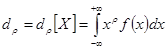 , очевидно, что математическое ожидание случайной величины есть первый начальный момент.
, очевидно, что математическое ожидание случайной величины есть первый начальный момент. 

 Математическое ожидание центрированной случайной величины равно 0.
Математическое ожидание центрированной случайной величины равно 0.






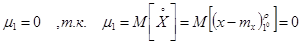








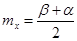 (математическое ожидание)
(математическое ожидание)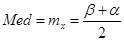 (медиана), Mod - не существует для данного распределения
(медиана), Mod - не существует для данного распределения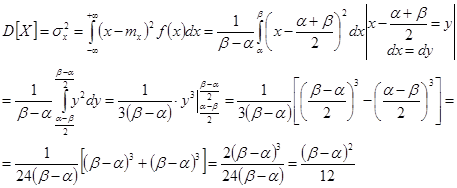
 (дисперсия),
(дисперсия),  (среднеквадратичное отклонение)
(среднеквадратичное отклонение) Говорят, что данное случайное распределение подчинено закону распределения Пуасона.
Говорят, что данное случайное распределение подчинено закону распределения Пуасона.



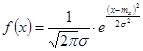



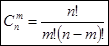
 ,
, 



