
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоремы сложения. Произведение независимых событийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определения вероятности, рассмотренные выше, относятся к приложениям теории вероятности. В фундаментальной теории вероятностей вероятность определяется аксиоматически и понимается как функция Р (А), определенная для случайных событий, удовлетворяющая аксиомам (даются в упрощенном виде): (А1) 0 £ Р (А) £ 1; (А2) Р (U) = 1, где U – достоверное событие; (А3) Р (А 1+ … + An) = Р (А 1) + … + Р (An), если А 1, …, An – попарно несовместные события. Аксиомы выбраны так, что они согласовываются с понятием вероятности, имеющим практический смысл. Из аксиом легко выводятся свойства вероятности. Теорема 1.5.1. Р (Æ) = 0. Теорема 1.5.2. Р ( Теорема 1.5.3. Р (А + В) = Р (А) + Р (В) – Р (АВ). При решении задач следует вводить события, вероятности которых следует найти, и события, вероятности которых даны или находятся по известным формулам. Выражаем искомые события через известные и находим их вероятности по подходящим формулам с помощью полученных выражений. Пример 1. Мишень состоит из круга и двух концентрических колец. Вероятности попадания в круг и кольца равны соответственно 0,2, 0,3 и 0,3. Какова вероятность промаха по мишени? Решение. Вводим события: А 1 – попадание в центральный круг; А 2 – попадание в первое кольцо; А 3 – попадание во второе кольцо; В – промах по мишени. Для нахождения искомой вероятности события В следует это событие выразить через события А 1, А 2, А 3, вероятности которых даны в условии задачи. Нетрудно понять, что В = Р ( Тогда Р (В) = 1 – Р ( Для нахождения вероятности произведения двух событийесть простая формула в случае, когда события независимы. В этом случае Р (АВ) = Р (А) Р (В). (1) События являются независимыми, например, если произошли в различных не связанных друг с другом испытаниях. Например, при двух подбрасываниях монеты вероятность выпадения «орла» при каждом подбрасывании никак не зависит от результата другого подбрасывания. В общем случае формула (1) принимается за определение независимых событий. Пример 2. Два охотника одновременно стреляют по зайцу. Вероятности попадания для них 0,4 и 0,3. Какова вероятность, что заяц будет подстрелен? Решение. Вводим события: А 1 – попадание первого охотника; А 2 – попадание второго охотника; В – заяц подстрелен. Имеем В = А 1 + А 2, поэтому Р (В) = Р (А 1 + А 2) = Р (А 1) + Р (А 2) – Р (А 1 А 2). Так как события А 1 и А 2 независимы, то Р (А 1 А 2) = Р (А 1) Р (А 2). Поэтому Р (В) = Р (А 1) + Р (А 2) – Р (А 1) Р (А 2) = 0,4 + 0,3 – 0,4 . 0,3 = 0,58. Пример 3. Три охотника одновременно стреляют по зайцу. Вероятности попадания для них 0,4, 0,5 и 0,3. Какова вероятность, что заяц будет подстрелен? Решение. Вводим события: Аi – попадание первого охотника, i = 1, 2, 3; В – заяц подстрелен. Ищем вероятность В через вероятность противоположного события, которое заключается в том, что все трое промахнулись:
Так как события в произведении независимы, то P ( Замечание. Этим же методом можно решать задачу в примере 2. Упражнения 5.1. Два стрелка одновременно стреляют по мишени. Вероятности попадания для них равны соответственно 0,4 и 0,5. Какова вероятность: а) хотя бы одного попадания; б) двух попаданий; в) ровно одного попадания; г) двух промахов? 5.2. Имеется два ящика, содержащих по 10 деталей. В первом ящике 8, во втором 7 стандартных деталей. Из каждого ящика наудачу вынимают по одной детали. Какова вероятность, что: а) они обе стандартные; б) хотя бы одна стандартная; в) ровно одна стандартная; г) они обе нестандартные? 5.3. Из колоды в 36 карт наудачу вынимается одна. Какова вероятность, что будет вынут туз или карта пиковой масти? 5.4. Какова вероятность, что наудачу выбранное натуральное число делится на 2 или на 5?
Условная вероятность Рассмотрим случай, когда события не являются независимыми. Пусть, например, студент Иванов подготовил к экзамену 20 вопросов из 25, и в билет входит один вопрос. Тогда вероятность того, что студенту достанется хороший билет (событие А) равна 20/25 = 4/5. Пусть теперь студент выбирает билет вторым в очереди. Тогда вероятность события А зависит от того, какой билет вытянул первый студент Петров. Если он вытянул билет, который знает Иванов (событие В), то для Иванова вероятность вытянуть хороший билет понижается: из 24 оставшихся вопросов он знает 19, и вероятность события А будет равна 19/24. Эта вероятность называется условной и обозначается РВ (А) или Р (А ï В) (читается «вероятность А при условии В»). Если же Петров вытянет билет, не подготовленный Ивановым (событие В общем случае условная вероятностьопределяется формулой РВ (А) = В частности, если события независимы, получаем РВ (А) = Из формулы (1) немедленно получаем формулу для вероятности произведения двух событий: Теорема 1.6.1. Р (АВ) = РВ (А) Р (В). Особенность этой формулы в том, что в левую ее часть А и В входят симметрично, а в правую – не симметрично. Поэтому можно поменять А и В местами, и получим другую формулу для вероятности произведения двух событий: Р (АВ) = Р (А) РА (В). При решении задач можно пользоваться любой из этих формул. Пример 1. Вероятность попадания в стоящее полено снежком равна 0,3. При попадании вероятность повалить полено равна 0,5. Какова вероятность, что полено будет повалено при одном бросании снежка? Решение. Вводим события: А – попадание в полено; В – полено повалено. В условии задачи даны вероятности: Р (А) = 0,3; РА (В) = 0,5. Поэтому искомая вероятность Р (АВ) = Р (А) РА (В) = 0,3 . 0,5 = 0,15. Теорема 1.6.1 может быть обобщена на случай произведения нескольких событий: Теорема 1.6.2. Р (А 1 А 2 … Аn) = Несмотря на кажущуюся сложность этой формулы, суть ее очень простая и легко проясняется на следующем примере: Пример 2. Из карточек с буквами выложено слово ТЕТЕРЕВ. Карточки перемешиваются, наугад извлекаются 4 карточки и выкладываются в ряд. Какова вероятность, что из них образуется слово ВЕЕР? Решение. Вводим события: А 1 – 1-я буква В; А 2 – 2-я буква Е; А 3 – 3-я буква Е; А 4 – 4-я буква Р; В – получилось слово ВЕЕР. Тогда В = А 1 А 2 А 3 А 4, и Р (В) = Р (В) = Упражнения 6.1. В урне 3 белых и 5 черных шаров. По очереди вынимаются два шара без возвращения. Какова вероятность, что: а) первый шар белый, а второй черный; б) первый шар черный, а второй белый? 6.2. В первой урне 3 белых и 5 черных шаров, во второй – 2 белых и 4 черных. Из первой урны во вторую случайным образом переложен один шар, затем извлечен шар из второй урны. Какова вероятность, что оба этих шара белые? 6.3. Слово «ананас» составлено из букв разрезной азбуки. Карточки с буквами перемешиваются и из них случайным образом берутся по очереди три карточки и выкладываются в ряд. Какова вероятность, что из них образуется слово «сан»? 6.4. Из карточек с буквами составлено слово «колокол». Карточки перемешиваются, из них случайным образом отбираются четыре и выкладываются в ряд. Какова вероятность, что они образуют слово «клок»? Формула полной вероятности При подсчете вероятностей имеет место важный случай, когда вероятность искомого события зависит от того, какое из нескольких возможных событий имело место. Определение. Полной группой событий называется совокупность попарно несовместных событий, в сумме дающих достоверное событие. Теорема 1.7.1 (формула полной вероятности). Пусть события Н 1, …, Нn, называемые гипотезами, образуют полную группу событий. Тогда вероятность любого события А вычисляется по формуле P (A) = На практике в качестве гипотез выбирают события, по разному влияющие на вероятность события А. Пример 1. На сборку поступают детали из двух цехов: 30% из первого и 70% из второго. В продукции первого цеха 3% брака, второго – 2%. Какова вероятность, что наудачу взятая деталь окажется бракованной? Решение. Вводим события: Н 1 – деталь поступила из первого цеха; Н 2 – деталь поступила из второго цеха; А – деталь бракованная. По формуле полной вероятности получаем P (A) = Часто представляет интерес обратная задача: найти вероятность данной гипотезы при условии, что итоговое событие произошло. Теорема 1.7.2 (формула Байеса). Пусть в условиях теоремы 1.7.1 событие произошло. Тогда вероятность гипотезы Hi вычисляется по формуле
где Р (А) вычисляется по формуле полной вероятности. Пример 2. В условиях примера 1 наудачу взятая деталь оказалась бракованной. Какова вероятность, что она из второго цеха? Решение. Пользуясь обозначениями из решения примера 1, получаем:
Упражнения 7.1. В магазин поступили партии обуви с двух фабрик: 30% с первой и 70% со второй. В продукции первой фабрики 30% обуви коричневого цвета, второй – 80%. Какова вероятность, что наудачу взятая пара обуви окажется коричневого цвета? 7.2. В группе спортсменов 20 лыжников и 8 бегунов. Вероятность выполнить квалификационную норму для лыжника равна 0,8, для бегуна – 0,7. Какова вероятность того, что наудачу отобранный спортсмен выполнит норму? 7.3. Из 50 деталей 18 изготовлены в первом цехе, 20 – во втором, остальные – в третьем. Первый и третий цеха дают продукцию отличного качества с вероятностью 0,9, второй – с вероятностью 0,6. Какова вероятность того, что наудачу взятая деталь будет отличного качества? 7.4. В первой коробке 3 белых и 4 черных шара, во второй – 5 белых и 2 черных. Из наудачу выбранной коробки случайным образом извлекли один шар. Какова вероятность, что он белый? 7.5. В первой коробке 3 белых и 4 черных шара, во второй – 5 белых и 2 черных. Из первой коробки во вторую случайным образом переложили один шар, перемешали и извлекли шар из второй коробки. Какова вероятность, что он белый? 7.6. В группе спортсменов 20 лыжников и 8 бегунов. Вероятность выполнить квалификационную норму для лыжника равна 0,8, для бегуна – 0,7. Наудачу отобранный спортсмен выполнил норму Какова вероятность, что он лыжник? 7.7. В первой коробке 3 белых и 4 черных шара, во второй – 5 белых и 2 черных. Из наудачу выбранной коробки случайным образом извлекли один шар, который оказался белым. Какова вероятность, что была выбрана первая коробка? 7.8. В первой коробке 3 белых и 4 черных шара, во второй – 5 белых и 2 черных. Из первой коробки во вторую случайным образом переложили один шар, перемешали и извлекли шар из второй коробки. Он оказался черным. Какова вероятность, что из первой коробки во вторую переложили черный шар? 7.9. Из 50 деталей 18 изготовлены в первом цехе, 20 – во втором, остальные – в третьем. Первый и третий цеха дают продукцию отличного качества с вероятностью 0,9, второй – с вероятностью 0,6. Наудачу взятая деталь оказалась отличного качества Какова вероятность, что она сделана в первом цехе?
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1314; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.184.124 (0.009 с.) |

 ) = 1 – Р (А).
) = 1 – Р (А).

 . Но для решения задачи гораздо проще найти сначала вероятность противоположного события
. Но для решения задачи гораздо проще найти сначала вероятность противоположного события 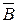 – попадание по мишени. Имеем
– попадание по мишени. Имеем  = 20/24 = 5/6.
= 20/24 = 5/6. . (1)
. (1) = Р (А).
= Р (А). .
. . Здесь каждая условная вероятность в произведении есть вероятность вытащить нужную букву при условии, что все предыдущие буквы вынуты правильно. Она вычисляется по классической формуле: в знаменателе стоит общее число оставшихся букв, в числителе – число нужных букв. Имеем
. Здесь каждая условная вероятность в произведении есть вероятность вытащить нужную букву при условии, что все предыдущие буквы вынуты правильно. Она вычисляется по классической формуле: в знаменателе стоит общее число оставшихся букв, в числителе – число нужных букв. Имеем .
. .
. = 0,3 . 0,03 + 0,7 . 0,02 = 0,009 + 0,014 = 0,023.
= 0,3 . 0,03 + 0,7 . 0,02 = 0,009 + 0,014 = 0,023. ,
, .
.


