Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема сложения вероятностей (для совместимых и несовместимых событий) и следствия из нее.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Т1: если события А и В несовместны, то вероятность суммы этих событий = сумме вероятностей. Р(А+В)=Р(А)+Р(В). Док-во: пусть m1 исходов благоприятствует событию А, а m2 событию В, тогда А+В благоприятствуют m1+m2, ® Р(А+В)= (m1+m2)\n = m1\n+m2\n=Р(А)+Р(В). Следствие 1: если события А1,А2,…,Аn образуют полную группу попарно несовместных событий, то сумма их вероятности = 1. Р(А1)+ Р(А2)+…+ Р(Аn)=1. Док-во: А1+А2+…+Аn - достоверно. Вероятность достоверного события равна 1. Следствие 2: Р(А)+Р( Замечание: если вероятность одного из противоположных событий обозначить р, то вероятность другого обозначим q. Итак p+q=1. Т2: если события А и В совместны, то Р(А+В)=Р(А)+Р(В) - Р(АВ). Док-во: пусть m1 исходов благоприятствуют событию А, m2 исходов благоприятствуют событию В, к исходов благоприятствуют событию АВ. Тогда событию А+В благоприятствуют (m1-k)+k+(m2-k)=m1+m2-k. Р(А+В)= (m1+m2-k)/n=m1/n+m2/n-k/n=P(A)+P(B)-P(AB). Условная вероятность. Теорема умножения вероятностей. Вероятность события А при условии что произошло событие В наз-ют условной вероятностью А при событии В и обозначают РB(A). Т еорема: вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность второго при условии, что произошло первое. Р(АВ)=Р(А)*РА(В) (1), Р(АВ)=Р(В)*РВ(А) (2). Док-во: Р(АВ)=к/n=m/n*k/m. m/n=P(A); k/m=PA(B), т.к. событие А произошло, то из всех возможных исходов остались только m благоприятных событию А, k из которых благоприятны событию В. Следствие: Р(А1А2…Аn)=Р(А1)*РА1(А2)*РА1А2(А3)*…*РА1А2…Аn-1(Аn). Независимые события. Теорема умножения вероятностей независимых событий. Опр: Событие А наз-ют независимым от события В, если его вероятность не зависит от того произошло или не произошло событие В, т.е. Р(А)=РВ(А). Из P(AB) = P(A)*PA(B) имеем Р(А)*РА(В)=Р(В)*РВ(А), если А не зависит от В, то сократив на равные выражения получаем Р(В)=РА(В), то В не зависит от А => понятие зависимости яв-ся взаимным. События А1,А2, …,Аn называют независимыми в совокупности или просто независ., если каждое из них и произведение люб. числа других попарно независ-мы. Напр. события А1, А2, А3 независ., если независ. следующие пары событий: А1 и А2, А1 и А3, А2 и А3, А1 и А2А3, … Т: вероятность произвед-я 2х независ-х событий = произв-ю их вероят-тей. Р(АВ)=Р(А)Р(В). Т. явл-ся следствием теор. умножения вероятностей. Следствие: если события А1,А2,….,Аn независимы в совокупности, то вероятность их произведения Р(А1*А2*…*Аn)=Р(А1)* Р(А2)*…* Р(Аn). Формула полной вероятности. Пусть событие А может произойти с одним и только с одним из попарно несовместных событий В1, В2,…,Вn, образующих полную группу. Т.к. заранее не известно какое из событий Вi произойдет, то их наз-ют гипотезами, очевидно что наступление события А равносильно наступлению одного из попарно несовместных событий АВ1 или АВ2 или... АВn, т.е. А=АВ1+АВ2+…+АВn. По теореме сложения для несовместных событий имеем: Р(А)=Р(АВ1)+Р(АВ2)+…+Р(АВn), по теореме умножения имеем: Р(А)=Р(В1)*РВ1(А)+Р(В2)*РВ2(А)+…+Р(Вn)*РВn(А). P(A)=∑P(BK)*PBK(A) Формула Байеса. Пусть событие А может произойти с одним и только с одним из попарно несовместных событий гипотез В1,…,Bn образующих полную группу. Пусть известно, что произошло событие А. Этот факт может повлиять на вероятности гипотез, т. е. произойдет их переоценка. Найдем усл. вер-ть гипотез при условии что произошло событие А. Р(АВi)=Р(А)*РА(Вi)=Р(Вi)*РВi(А); РА(Вi)= Р(Вi)* РВi(А)/Р(А), или используя формулу полной вероятности:
Независимые повторные испытания, формула Бернулли. Пусть произведено n независ. Испытаний. Вероятн. Появл. События А в каждом испытании равна р, а значит вероятность его непоявления q=1-p. Найдем вероятность события В, сост. в том, что в этих испытаниях событие А появится m раз, вероятн. событ. В обознач. Pn(m)=P(B). Аi - появление события А в i - том испытании
По формуле бинома Ньютона имеем:
Локальная теорема Лапласа. Если вероятность появления события А в каждом из n независимых испытаний постоянно и равна p (0<p<1), то вероятность появления события А в этих испытаниях m раз приближенно =
где
Для функции
составлены специальные таблицы при х из[0, 4), при x<0 пользуются четностью, при x>=4 полагают Теорема Пуассона. Ф-лу используют если p или d мало. Пусть для опред-ти мало p, и вер-ть появления события А удовлетвор. Условию np=λ-const, с такой ситуацией встреч при редких явлениях. Теорема: Пусть вероятность появления события А в серии из n независимых испыт. равна p=λ/n, тогда вер. появления события А в этой серии m раз удовл. условию:
(далее переписать эту формулу без предела). Ей пользуются при больших n и малых p и λ £10.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 791; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.54.147 (0.006 с.) |

 )=1 (сумма вероятности противоп. соб.=1).
)=1 (сумма вероятности противоп. соб.=1).
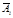 -не появление А в i- ом испытании.
-не появление А в i- ом испытании. 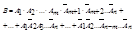 Здесь в каждом произведении события Аi входит n раз, а Ai (с чертой) m-n раз. Число таких комбинаций столько, сколькими способами м. выбрать из n испытаний те m в котор. произошло событ. А. Вероятность каждой такой комбинации по теореме о умножении независимых событий=рmqn-m,
Здесь в каждом произведении события Аi входит n раз, а Ai (с чертой) m-n раз. Число таких комбинаций столько, сколькими способами м. выбрать из n испытаний те m в котор. произошло событ. А. Вероятность каждой такой комбинации по теореме о умножении независимых событий=рmqn-m,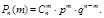
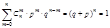
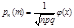


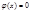 , т.к. функция быстро убывает. Ф-я четная. Формулой пользуются, если npq³10. Формула Лапласа дает более точный рез-т при р близких к 0,5, если p или q мало то погрешность м.б. большой. В этих случаях используют ф-лу Пуассона.
, т.к. функция быстро убывает. Ф-я четная. Формулой пользуются, если npq³10. Формула Лапласа дает более точный рез-т при р близких к 0,5, если p или q мало то погрешность м.б. большой. В этих случаях используют ф-лу Пуассона.