
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предел функции. Основные теоремы о пределахСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Предел функции. Основные теоремы о пределах Предел функции Предел функции при Пусть функция f (x) определена на некотором множестве X и пусть дана точка
сходящуюся к
и можно ставить вопрос о существовании её предела. Определение 1. Число A называется пределом функции f (x) в точке Символически это записывается так:
Пример 1. Найти предел функции Решение. Подставляем вместо x значение 0. Получаем:
Итак, предел данной функции при Предел функции при Кроме рассмотренного понятия предела функции при Определение 2. Число A называется пределом функции f (x) при Символически это записывается так: Определение 3. Число A называется пределом функции f (x) при Символически это записывается так:
Пример 2. Найти предел функции Решение. Подставляем вместо x бесконечность. Получаем, что последовательность значений функции является бесконечно малой величиной и поэтому имеет предел, равный нулю:
Для наглядности и убедительности, решая данный пример в черновике, можете подставить вместо x супербольшое число. При делении получите супермалое число.
Основные теоремы о пределах Теорема 1. (о единственности предела функции). Функция не может иметь более одного предела. Следствие. Если две функции f (x) и g (x) равны в некоторой окрестности точки Теорема 2. Если функции f(x) и g(x) имеют пределы в точке 1) предел алгебраической суммы функций равен алгебраической сумме пределов слагаемых, т.е.
2) предел произведения функций равен произведению пределов сомножителей, т.е.
3) предел частного двух функций равен частному от деления предела делимого на предел делителя, если предел делителя не равен нулю, т.е.
Замечание. Формулы (3) и (4) справедливы для любого конечного числа функций. Следствие 1. Предел постоянной равен самой постоянной, т.е.
Следствие 2. Постоянный множитель можно выносить за знак предела, т.е.
Пример 3. Найти предел:
Решение.
Пример 4. Найти предел:
Решение. Предварительно убедимся, что предел делителя не равен нулю:
Таким образом, формула (5) применима и, значит, Теорема 3 (о пределе сложной функции). Если существует конечный предел
а функция f(u) непрерывна в точке
Другими словами, для непрерывных функций символы предела и функции можно поменять местами. Непосредственное применение теорем о пределах, однако, не всегда приводит к цели. Например, нельзя применить теорему о пределе частного, если предел делителя равен нулю. В таких случаях необходимо предварительно тождественно преобразовать функцию, чтобы иметь возможность применить следствие из теоремы 1. Пример 5. Найти предел:
Решение. Теорема о пределе частного здесь неприменима, так как
Преобразуем заданную дробь, разложив числитель и знаменатель на множители. В числителе получим
где
корни квадратного трёхчлена (если Вы забыли, как решать квадратные уравнения, то Вам сюда). Теперь сократим дробь и, используя следствие из теоремы 1, вычислим предел данной функции:
Производная. Понятие производной При решении различных задач геометрии, механики, физики и других отраслей знания возникла необходимость с помощью одного и того же аналитического процесса из данной функции y=f(x) получать новую функцию, которую называют производной функцией (или просто производной) данной функции f(x) и обозначают символом Тот процесс, с помощью которого из данной функции f(x) получают новую функцию f ' (x), называют дифференцированием и состоит он из следующих трех шагов: 1) даем аргументу x приращение ??x и определяем соответствующее приращение функции ??y = f(x+??x) -f(x); 2) составляем отношение 3) считая x постоянным, а ??x 0, находим, который обозначаем через f ' (x), как бы подчеркивая тем самым, что полученная функция зависит лишь от того значения x, при котором мы переходим к пределу. Определение: Производной y ' =f ' (x) данной функции y=f(x) при данном x называется предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю, если, конечно, этот предел существует, т.е. конечен. Таким образом,, или Заметим, что если при некотором значении x, например при x=a, отношение при ??x 0 не стремится к конечному пределу, то в этом случае говорят, что функция f(x) при x=a (или в точке x=a) не имеет производной или не дифференцируема в точке x=a. Правила дифференцирования
Производная степенно-показательной функции , где. . Логарифмическое дифференцирование. Пусть дана функция. При этом предполагается, что функция не обращается в нуль в точке. Покажем один из способов нахождения производной функции, если очень сложная функция и по обычным правилам дифференцирования найти производную затруднительно. Так как по первоначальному предположению не равна нулю в точке, где ищется ее производная, то найдем новую функцию и вычислим ее производную (1) Отношение называется логарифмической производной функции. Из формулы (1) получаем . Или Формула (2) дает простой способ нахождения производной функции. Производные высших порядков Ясно, что производная функции y =f (x) есть также функция от x: Если функция f ' (x) дифференцируема, то её производная обозначается символом y'' =f '' (x) и называется второй производной функции f(x) или производной функции f(x) второго порядка. Пользуясь обозначением можем написать Очень удобно пользоваться также обозначением, указывающим, что функция y=f(x) была продифференцирована по x два раза. Вообще n -я производная или производная n -го порядка функции y=f(x) обозначается символами Дифференцируя производную первого порядка, можно получить производную второго порядка, а, дифференцируя полученную функцию, получаем производную третьего порядка и т.д. Тогда возникает вопрос: сколько производных высших порядков можно получить в случае произвольной функции. Например: 1);;;...; ;. Разные функции ведут себя по-разному при многократном дифференцировании. Одни имеют конечное количество производных высших порядков, другие - переходят сами в себя, а третьи, хотя и дифференцируемы бесконечное количество раз, но порождают новые функции, отличные от исходной. Однако все сформулированные теоремы о производных первых порядков выполняются для производных высших порядков. 18. 6. Понятие первообразной и неопределенного интеграла. Свойства неопределенного интеграла.
Найти первообразную – это значит «взять интеграл» Интегрирование – это операция обратная дифференцированию. Первообразной функцией для данной функции называется такая функция
интеграл функция
________________________________________________________________
________________________________________________________________
Вычисление площадей F - площадь криволинейной трапеции, ограниченной линиями y = 0, x = a, x = b и y = f (x), где f (x) - непрерывная, положительная функция, выраженная формулой
Приведем два примера применения этой формулы. Пример 1. Так как уравнение окружности (см. Рис. 1) с центром в начале координат и радиусом R есть x 2 + y 2 = R 2, то уравнение верхней полуокружности имеет вид
Поэтому площадь заштрихованного на чертеже полукруга равна
Полагая x = R sin t, приводим этот интеграл к виду
Поэтому площадь всего круга равна πR 2. Определения и понятия теории дифференциальных уравнений. Эта статья является отправной точкой в изучении теории дифференциальных уравнений. Здесь собраны основные определения и понятия, которые будут постоянно фигурировать в тексте. Для лучшего усвоения и понимания определения снабжены примерами. Дифференциальное уравнение (ДУ) – это уравнение, в которое входит неизвестная функция под знаком производной или дифференциала. Если неизвестная функция является функцией одной переменной, то дифференциальное уравнение называют обыкновенным (сокращенно ОДУ – обыкновенное дифференциальное уравнение). Если же неизвестная функция есть функция многих переменных, то дифференциальное уравнение называют уравнением в частных производных. Максимальный порядок производной неизвестной функции, входящей в дифференциальное уравнение, называется порядком дифференциального уравнения. Вот примеры ОДУ первого, второго и пятого порядков соответственно В качестве примеров уравнений в частных производных второго порядка приведем Далее мы будем рассматривать только обыкновенные дифференциальные уравнения n-ого порядка вида Процесс нахождения решений дифференциального уравнения называется интегрированием дифференциального уравнения. Решение дифференциального уравнения - это неявно заданная функция Ф(x, y) = 0 (в некоторых случаях функцию y можно выразить через аргумент x явно), которая обращает дифференциальное уравнение в тождество. ОБРАТИТЕ ВНИМАНИЕ. Решение дифференциального уравнения всегда ищется на заранее заданном интервале X. Почему мы об этом говорим отдельно? Да потому что в условиях многих задач об интервале X не упоминают. То есть, обычно условие задач формулируется так: «найдите решение обыкновенного дифференциального уравнения Решение дифференциального уравнения часто называют интегралом дифференциального уравнения. Функции Одним из решений дифференциального уравнения Общее решение дифференциального уравнения – это множество решений, содержащее все без исключения решения этого дифференциального уравнения. Общее решение дифференциального уравнения еще называют общим интегралом дифференциального уравнения. Вернемся к примеру. Общее решение дифференциального уравнения Если решение дифференциального уравнения удовлетворяет изначально заданным дополнительным условиям, то его называют частным решением дифференциального уравнения. Формула полной вероятности Пусть некоторое событие может произойти вместе с одним из несовместных событий, составляющих полную группу событий. Пусть известны вероятности этих событий и условные вероятности наступления события при наступлении события. Теорема. Вероятность события, которое может произойти вместе с одним из событий, равна сумме парных произведений вероятностей каждого из этих событий на соответствующие им условные вероятности наступления события. Фактически эта формула полной вероятности уже использовалась при решении примеров, приведенных выше, например, в задаче с револьвером. Доказательство. Т.к. события образуют полную группу событий, то событие можно представить в виде следующей суммы: Т.к. события несовместны, то и события тоже несовместны. Тогда можно применить теорему о сложении вероятностей несовместных событий: При этом Окончательно получаем: Теорема доказана. Пример. Один из трех стрелков производит два выстрела. Вероятность попадания в цель при одном выстреле для первого стрелка равна, для второго -, для третьего -. Найти вероятность того, что в цель попадут два раза. Вероятность того, что выстрелы производит первый, второй или третий стрелок равна. Вероятности того, что один из стрелков, производящих выстрелы, два раза попадает в цель, равны: - для первого стрелка: - для второго стрелка: - для третьего стрелка: Искомая вероятность равна: §6. Теоремы сложения и умножения вероятностей Суммой двух событий и называется событие, состоящее в появлении хотя бы одного из событий или. Теорема сложения вероятностей. Вероятность суммы двух несовместимых событий равна сумме вероятностей этих событий: В случае, когда события и совместны, вер-ть их суммы выражается формулой Где - произведение событий и. Два события называются зависимыми, если вероятность одного из них зависит от наступления или не наступления другого. в случае зависимых событий вводится понятие условной вероятности события. Условной вероятностью события называется вероятность события, вычисленная при условии, что событие произошло. Аналогично через обозначается условная вероятность события при условии, что событие наступило. Произведением двух событий и называется событие, состоящее в совместном появлении события и события. Предел функции. Основные теоремы о пределах Предел функции Предел функции при Пусть функция f (x) определена на некотором множестве X и пусть дана точка
сходящуюся к
и можно ставить вопрос о существовании её предела. Определение 1. Число A называется пределом функции f (x) в точке Символически это записывается так:
Пример 1. Найти предел функции Решение. Подставляем вместо x значение 0. Получаем:
Итак, предел данной функции при Предел функции при Кроме рассмотренного понятия предела функции при Определение 2. Число A называется пределом функции f (x) при Символически это записывается так: Определение 3. Число A называется пределом функции f (x) при Символически это записывается так:
Пример 2. Найти предел функции Решение. Подставляем вместо x бесконечность. Получаем, что последовательность значений функции является бесконечно малой величиной и поэтому имеет предел, равный нулю:
Для наглядности и убедительности, решая данный пример в черновике, можете подставить вместо x супербольшое число. При делении получите супермалое число.
Основные теоремы о пределах Теорема 1. (о единственности предела функции). Функция не может иметь более одного предела. Следствие. Если две функции f (x) и g (x) равны в некоторой окрестности точки Теорема 2. Если функции f(x) и g(x) имеют пределы в точке 1) предел алгебраической суммы функций равен алгебраической сумме пределов слагаемых, т.е.
2) предел произведения функций равен произведению пределов сомножителей, т.е.
3) предел частного двух функций равен частному от деления предела делимого на предел делителя, если предел делителя не равен нулю, т.е.
Замечание. Формулы (3) и (4) справедливы для любого конечного числа функций. Следствие 1. Предел постоянной равен самой постоянной, т.е.
Следствие 2. Постоянный множитель можно выносить за знак предела, т.е.
Пример 3. Найти предел:
Решение.
Пример 4. Найти предел:
Решение. Предварительно убедимся, что предел делителя не равен нулю:
Таким образом, формула (5) применима и, значит, Теорема 3 (о пределе сложной функции). Если существует конечный предел
а функция f(u) непрерывна в точке
Другими словами, для непрерывных функций символы предела и функции можно поменять местами. Непосредственное применение теорем о пределах, однако, не всегда приводит к цели. Например, нельзя применить теорему о пределе частного, если предел делителя равен нулю. В таких случаях необходимо предварительно тождественно преобразовать функцию, чтобы иметь возможность применить следствие из теоремы 1. Пример 5. Найти предел:
Решение. Теорема о пределе частного здесь неприменима, так как
Преобразуем заданную дробь, разложив числитель и знаменатель на множители. В числителе получим
где
корни квадратного трёхчлена (если Вы забыли, как решать квадратные уравнения, то Вам сюда). Теперь сократим дробь и, используя следствие из теоремы 1, вычислим предел данной функции:
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 2725; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.014 с.) |


 . Возьмём из X последовательность точек, отличных от
. Возьмём из X последовательность точек, отличных от 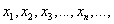 (1)
(1)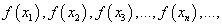 (2)
(2) (или при
(или при 
 при
при  .
. .
. , при
, при  и при
и при 
 .
. которой положительны (отрицательны), соответствующая последовательность (2) значений функции сходится к A.
которой положительны (отрицательны), соответствующая последовательность (2) значений функции сходится к A.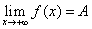 (
( ).
).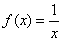 при
при  .
.
 , за исключением, может быть, самой точки
, за исключением, может быть, самой точки  , либо обе не имеют предела в этой точке.
, либо обе не имеют предела в этой точке. (3)
(3)
 (4)
(4) (5)
(5)







 , то
, то





 , производная которой равна исходной функции
, производная которой равна исходной функции 




 - НЕОПРЕДЕЛЕННЫЙ интеграл
- НЕОПРЕДЕЛЕННЫЙ интеграл



























 или
или  , где Ф(x, y) = 0 неизвестная функция, заданная неявно (когда возможно, будем ее записывать в явном представлении y = f(x)).
, где Ф(x, y) = 0 неизвестная функция, заданная неявно (когда возможно, будем ее записывать в явном представлении y = f(x)). или
или  можно назвать решением дифференциального уравнения
можно назвать решением дифференциального уравнения  .
. является функция
является функция  . Действительно, подставив эту функцию в исходное уравнение, получим тождество
. Действительно, подставив эту функцию в исходное уравнение, получим тождество 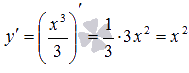 . Несложно заметить, что другим решением этого ОДУ является, например,
. Несложно заметить, что другим решением этого ОДУ является, например,  . Таким образом, дифференциальные уравнения могут иметь множество решений.
. Таким образом, дифференциальные уравнения могут иметь множество решений. или
или  , где C – произвольная постоянная. Выше мы указали два решения этого ОДУ, которые получаются из общего интеграла дифференциального уравнения
, где C – произвольная постоянная. Выше мы указали два решения этого ОДУ, которые получаются из общего интеграла дифференциального уравнения 


