
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные теоремы о пределах.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Основные теоремы о пределах. . Теорема 2. Если функцииf(x) и g(x) имеют пределы в точке 1) предел алгебраической суммы функций равен алгебраической сумме пределов слагаемых, т.е.
2) предел произведения функций равен произведению пределов сомножителей, т.е.
3) предел частного двух функций равен частному от деления предела делимого на предел делителя, если предел делителя не равен нулю, т.е.
Замечание. Формулы (2) и (3) справедливы для любого конечного числа функций. Следствие 1. Предел постоянной равен самой постоянной, т.е. Следствие 2. Постоянный множитель можно выносить за знак предела, т.е. Теорема 3 (о пределе сложной функции). Если существует конечный предел а функция f(u) непрерывна в точке Другими словами, для непрерывных функций символы предела и функции можно поменять местами. 33. Первый замечательный предел (с выводом). Первый замечательный предел: Главное, что Х стремится к 0.
Следствия § § § § § Из первого замечательного предела следует эквивалентность при х →0 следующих бесконечно малых величин: ах, sin ax; tg ax; arcsin ax; arctg ax. Это означает, что предел отношения двух любых из этих функций при х →0 равен 1. § С помощью этого соотношения можно вычислить массу других неопределенностей, которые без применения первого замечательного предела вычислялись бы сложнее.
34. Второй замечательный предел. Определение и геометрический смысл производной. Произво́дная — произведённая, образованная от другой, простейшей или основной величины, формы, категории. Произво́дная — функция, являющаяся результатом применения той или иной операции дифференцирования к исходной функции. Геометрический смысл производной. Производная в точке x 0 равна угловому коэффициенту касательной к графику функции y = f (x) в этой точке.
Интервалы выпуклости и вогнутости, точки перегиба. График функции y = f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале. График функции y = f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале. Теорема. Пусть y = f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b) вторая производная функции y = f(x) отрицательная, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый, если же f ''(x) > 0 – вогнутый.
Теорема. Пусть кривая определяется уравнением y = f(x). Если f ''(x 0) = 0 или f ''(x 0) не существует и при переходе через значение x = x0 производная f ''(x) меняет знак, то точка графика функции с абсциссой x = x0 есть точка перегиба. Асимптоты. Прямая называется асимптотой графика функции y = f(x), если расстояние от переменной точки M графика до этой прямой при удалении точки M в бесконечность стремится к нулю, т.е. точка графика функции при своем стремлении в бесконечность должна неограниченно приближаться к асимптоте. вертикальной асимптотой графика функции y = f(x) называется прямая, если f(x) → ∞ хотя бы при одном из условий x → x0 – 0 или x → x0 + 0, x = x0 Следовательно, для отыскания вертикальных асимптот графика функции y = f(x) нужно найти те значения x = x0, при которых функция обращается в бесконечность (терпит бесконечный разрыв). Тогда вертикальная асимптота имеет уравнение x = x0. Теорема. Прямая y = kx + b служит наклонной асимптотой при x → +∞ для графика функции y = f(x) тогда и только тогда, когда 54.Формула Тейлора:
(Rn(x) - остаточный член формулы Тейлора). Многочлен Тейлора порядка n:
В форме Лагранжа:
В форме Коши:
В форме Пеано:
В интегральной форме:
55. Формула Тейлора для любой функции, разложение функций ex, sinx. Основные разложения в ряд Тейлора
56. Функции многих переменных: способы задания, область определения, непрерывность и разрывы.
1. Обозначим через D некоторое множество точек в п -мерном пространстве. Если задан закон f, в силу которого каждой точке М (х;...; х) D ставится в соответствие число и, то говорят, что на множестве D определена функция и = f (х;...; х). Множество точек М (х;...; х), для которых функция и = f (х;...; х) определена, называют областью определения этой функции и обозначают D (f). Функции многих переменных можно обозначать одним символом и = f (М), указывая размерность пространства, которому принадлежит точка М. Функции двух переменных можно изобразить графически в виде некоторой поверхности. Графиком функции двух переменных z=f (х; у) в прямоугольной системе координат Оху называется геометрическое место точек в трехмерном пространстве, координаты которых (х; у; z) удовлетворяют уравнению z=f (х; у).
Функция и = f (М) называется непрерывной в точке М, если = f (М). Функция и = f (М) называется непрерывной на множестве D, если она непрерывна в каждой точке МD. Точки, в которых непрерывность функции нарушается, называются точками разрыва функция. Точки разрыва могут быть изолированными, создавать линии разрыва, поверхности разрыва и т. д.Например, функция z= имеет разрыв в точке (0;0), а функция z= имеет разрыв на параболе Метод наименьших квадратов. Такая модель в общем виде может быть представлена уравнением (1.2): yt = a0 + a1 х1t +...+ an хnt + εt. Исходными данными при оценке параметров a0 , a1 ,..., an является вектор значений зависимой переменной y = (y1, y2,..., yT)' и матрица значений независимых переменных
в которой первый столбец, состоящий из единиц, соответствует коэффициенту модели Название свое метод наименьших квадратов получил, исходя из основного принципа, которому должны удовлетворять полученные на его основе оценки параметров: сумма квадратов ошибки модели должна быть минимальной. |
63. Производная по направлению.
Производная по направлению — это обобщение понятия производной на случай функции нескольких переменных. Производная по направлению показывает, насколько быстро функция изменяется при движении вдоль заданного направления.
Производная функции одной переменной показывает, как изменяется её значение при малом изменении аргумента. Если мы попытаемся по аналогии определить производную функции многих переменных, то столкнёмся с трудностью: в этом случае изменение аргумента (то есть точки в пространстве) может происходить в разных направлениях, и при этом будут получаться разные значения производной. Именно это соображение и приводит к определению производной по направлению.
Рассмотрим функцию  от
от  аргументов в окрестности точки
аргументов в окрестности точки  . Для любого единичного вектора
. Для любого единичного вектора  определим производную функции
определим производную функции  в точке
в точке 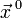 по направлению
по направлению  следующим образом:
следующим образом:

Значение этого выражения показывает, как быстро меняется значение функции при сдвиге аргумента в направлении вектора  .
.
Если направление сонаправленно с координатной осью, то производная по направлению совпадает с частной производной по этой координате.
Градиент.
Градиент — характеристика, показывающая направление наискорейшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой. Например, если взять высоту поверхности Земли над уровнем моря (2-мерное пространство), то её градиент в каждой точке поверхности будет показывать «в горку».
Как видно из объяснения, градиент является векторной функцией, а величина, которую он характеризует — функцией скалярной.Формально, для случая трёхмерного пространства, градиентом называется векторная функция с компонентами  ,
,  ,
,  , где φ — некоторая скалярная функция координат x, y, z.
, где φ — некоторая скалярная функция координат x, y, z.
Если φ — функция n переменных  , то её градиентом будет n-мерный вектор
, то её градиентом будет n-мерный вектор
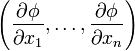 ,
,
компоненты которого равны частным производным φ по всем её аргументам.
Градиент обозначается gradφ или, с использованием оператора набла,  .
.
Из определения градиента следует, что:

Свойства:
§ 
Линейность
§ 
§ 
Правило Лейбница
|
|
§  , где
, где  — скалярное произведение векторов
— скалярное произведение векторов  и
и  .
.
Связь с градиентом:Производную по направлению дифференциируемой по совокупности переменных функции можно рассматривать как проекцию градиента функции на это направление, или иначе, как скалярное произведение градиента на орт направления:
 ,
,
где  — орт направления. Отсюда следует, что максимальное значение в точке производная по направлению принимает, если направление совпадает с направлением градиента функции в данной точке. Также видно, что значение производной по направлению не зависит от длины вектора
— орт направления. Отсюда следует, что максимальное значение в точке производная по направлению принимает, если направление совпадает с направлением градиента функции в данной точке. Также видно, что значение производной по направлению не зависит от длины вектора  .
.
Основные теоремы о пределах.
. Теорема 2. Если функцииf(x) и g(x) имеют пределы в точке  , то:
, то:
1) предел алгебраической суммы функций равен алгебраической сумме пределов слагаемых, т.е.
 (2)
(2)
2) предел произведения функций равен произведению пределов сомножителей, т.е.


 (3)
(3)
3) предел частного двух функций равен частному от деления предела делимого на предел делителя, если предел делителя не равен нулю, т.е.
 (4)
(4)
Замечание. Формулы (2) и (3) справедливы для любого конечного числа функций.
Следствие 1. Предел постоянной равен самой постоянной, т.е. 
Следствие 2. Постоянный множитель можно выносить за знак предела, т.е. 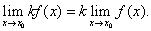
Теорема 3 (о пределе сложной функции). Если существует конечный предел 
а функция f(u) непрерывна в точке  , то
, то 
Другими словами, для непрерывных функций символы предела и функции можно поменять местами.
33. Первый замечательный предел (с выводом).
|
| Поделиться: |

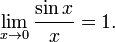

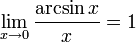


 . Аналогичное утверждение верно и при x → –∞.
. Аналогичное утверждение верно и при x → –∞.
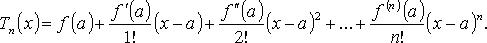
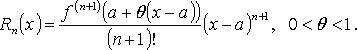
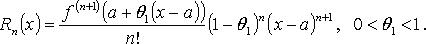
 при
при 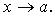

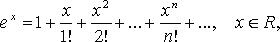
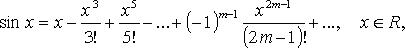
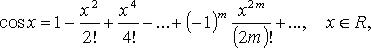

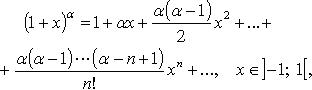
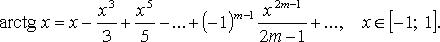

 .
.


