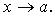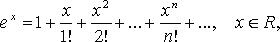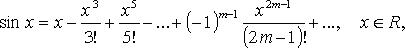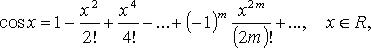Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Экстремумы (необходимое условие существования с док.).Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Определение. Точка x0 называется точкой минимума функции f, если для всех x из некоторой окрестности x0 выполняется неравенство f(x) ≥ f(x0. Определение. Точка x0 называется точкой максимума функции f, если для всех x из некоторой окрестности x0 выполняется неравенство f(x) ≤ f(x0. Для точек минимума и максимума функции есть общее определение - точки экстремума. Значение функции в этих точках соответственно назывется максимумом или минимумом этой функции. Общее название - экстремум функции. Точки максимума обычно обозначают xmax, а точки минимума - xmin Доказательство. Докажем необходимость условия существования максимума. Пусть f '(x) = 0, f ''(x) > 0. Экстремумы (достаточное условие существования без док.), схема исследования на экстремум Теорема 1. Если функция f(x) имеет в каждой точке интервала (a, b) неотрицательную производную, то она является неубывающей функцией в этом интервале. Теорема 2. Если функция f(x) в каждой точке интервала (a, b) имеет неположительную производную, то она является невозрастающей функцией в этом интервале. Теорема 4. (второй достаточный признак существования экстремума функции). Если в точке x0 первая производная f '(x) функции f(x) обращается в нуль, а её вторая производная f ''(x) отлична от нуля, то в точке x0 функция f(x) достигает экстремума (минимума, если f ''(x) > 0, и максимума, если f ''(x) < 0). Предполагается, что f ''(x) непрерывна в точке x0 и ее окрестности. Алгоритм исследования функции на экстремум: 1)Найти производную функции. Интервалы выпуклости и вогнутости, точки перегиба. График функции y = f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале. График функции y = f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале. Теорема. Пусть y = f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b) вторая производная функции y = f(x) отрицательная, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый, если же f ''(x) > 0 – вогнутый. Теорема. Пусть кривая определяется уравнением y = f(x). Если f ''(x 0) = 0 или f ''(x 0) не существует и при переходе через значение x = x0 производная f ''(x) меняет знак, то точка графика функции с абсциссой x = x0 есть точка перегиба. Асимптоты. Прямая называется асимптотой графика функции y = f(x), если расстояние от переменной точки M графика до этой прямой при удалении точки M в бесконечность стремится к нулю, т.е. точка графика функции при своем стремлении в бесконечность должна неограниченно приближаться к асимптоте. вертикальной асимптотой графика функции y = f(x) называется прямая, если f(x) → ∞ хотя бы при одном из условий x → x0 – 0 или x → x0 + 0, x = x0 Следовательно, для отыскания вертикальных асимптот графика функции y = f(x) нужно найти те значения x = x0, при которых функция обращается в бесконечность (терпит бесконечный разрыв). Тогда вертикальная асимптота имеет уравнение x = x0. Теорема. Прямая y = kx + b служит наклонной асимптотой при x → +∞ для графика функции y = f(x) тогда и только тогда, когда 54.Формула Тейлора:
(Rn(x) - остаточный член формулы Тейлора). Многочлен Тейлора порядка n:
В форме Лагранжа:
В форме Коши:
В форме Пеано:
В интегральной форме:
55. Формула Тейлора для любой функции, разложение функций ex, sinx. Основные разложения в ряд Тейлора
56. Функции многих переменных: способы задания, область определения, непрерывность и разрывы.
1. Обозначим через D некоторое множество точек в п -мерном пространстве. Если задан закон f, в силу которого каждой точке М (х;...; х) D ставится в соответствие число и, то говорят, что на множестве D определена функция и = f (х;...; х). Множество точек М (х;...; х), для которых функция и = f (х;...; х) определена, называют областью определения этой функции и обозначают D (f). Функции многих переменных можно обозначать одним символом и = f (М), указывая размерность пространства, которому принадлежит точка М. Функции двух переменных можно изобразить графически в виде некоторой поверхности. Графиком функции двух переменных z=f (х; у) в прямоугольной системе координат Оху называется геометрическое место точек в трехмерном пространстве, координаты которых (х; у; z) удовлетворяют уравнению z=f (х; у). Функция и = f (М) называется непрерывной в точке М, если = f (М). Функция и = f (М) называется непрерывной на множестве D, если она непрерывна в каждой точке МD. Точки, в которых непрерывность функции нарушается, называются точками разрыва функция. Точки разрыва могут быть изолированными, создавать линии разрыва, поверхности разрыва и т. д.Например, функция z= имеет разрыв в точке (0;0), а функция z= имеет разрыв на параболе
|
||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1478; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 . Аналогичное утверждение верно и при x → –∞.
. Аналогичное утверждение верно и при x → –∞.
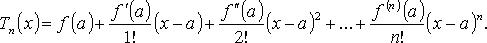
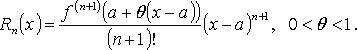
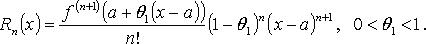
 при
при