
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принятие решений в условиях неопределенности и рискаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В этих ситуациях возможно использование теории статистических решений. Эта теория близка по идеям к теории игр, от которой отличается тем, что неопределенность не имеет конфликтной окраски — никто никому не противодействует. В задачах теории статистических решений неизвестные условия операции (смысл термина из исследования операций) зависят от объективной действительности, которая называется в теории статистических решений «природой». В игре против сознательного противника элемент неопределенности отчасти снимается тем, что мы «думаем» за противника, принимаем самое благоприятное решение для нас самих. В игре с «природой» это не подходит, кто ее знает, как она себя поведет. Поэтому часто получается, что при принятии решения мы рискуем. Риск является важным элементом человеческой деятельности. Мы знаем, что тот, кто умеет рисковать, оказывается в выигрыше, и что осторожность не всегда приводит к успеху, а иногда приводит прямо к проигрышу. Каков риск политика, когда он поддерживает или отвергает ту или иную кандидатуру перед выборами? Чем рискуют экономисты, предлагая снизить налоги и т. д. Все они должны уметь правильно оценить степень риска своих действий и действовать расчетливо и обоснованно. Риск, понимаемый как действие в надежде на благоприятный исход, возникает по ряду причин, которые относятся к факторам неопределенности. Виды неопределенности были достаточно полно сформулированы в п. 4.2. Основные критерии, которые используются в теории статистических решений и которые реализуют способы выбора оптимальных решений, рассмотрим на конкретном примере. Дополним пример в п. 5.4.5 еще одной альтернативой: предположим, что вы можете поехать в Ригу на автомобиле. Для этой альтернативы погодные условия тоже будут влиять, в частности, на выбор скорости вождения. К другой неопределенности можно отнести неопределенность потери времени при прохождении проверки документов и осмотра автомобиля на границе. Измененные условия задачи представим в табл. 5.5.1. Таблица 5.5.1.
Пусть мы хотим выбрать при этих двух погодных условиях наилучший для нас вариант. Сначала преобразуем по аналогии с тем, как делали в предыдущем пункте, эту матрицу, прибавив ко всем элементам число 28. Получим преобразованную матрицу полезности || иli ||, где: L — альтернативы, J — возможные условия, представленную в виде таблицы 5.5.2. Таблица 5.5.2.
Теперь рассмотрим несколько вариантов решения сформулированной задачи. 5.5.1. Равновероятный выбор. Предположим, что нам неизвестен прогноз погоды, тогда будем считать, что на период нашей поездки возможна как ясная погода, так и густой туман, т. е. эти два события равновероятны. Чтобы определить ожидаемую полезность первого выбора (поезда), надо перемножить соответствующие элементы строки матрицы полезности на соответствующие элементы матрицы вероятности и результаты сложить. Так же поступают при вычислении ожидаемой полезности второго действия (выбор самолета) и третьего (выбор автомобиля): Поезд W 1 = 16 ∙ 0.5 + 16 ∙ 0.5 = 16 Самолет W 2 = 0 ∙ 0.5 + 26 ∙ 0.5 = 13 Автомобиль W 3 = 15 ∙ 0.5 + 19 ∙ 0.5=17 Так как W 3 = max (W 1, W 2, W 3), то в этом случае третий вариант (выбор автомобиля) будет при заданных условиях наилучшим. 5.5.2. Вероятный выбор. Предположим, что у нас имеется информация из компетентных источников прогноза погоды на дни нашей поездки. Вероятность тумана — 0.3, а вероятность ясной погоды — 0.7. Проведем расчеты по использованному в предыдущем пункте алгоритму. Поезд W 1 = 16 ∙ 0.3 + 16 ∙ 0.7 = 16 Самолет W 2 = 0 ∙ 0.3 + 26 ∙ 0.7 = 18.2 Автомобиль W 3 = 15 ∙ 0.3 + 19 ∙ 0.7 = 17.8 Для этого способа максимальная полезность достигается для второго варианта — выбора самолета. Посмотрим, как изменится результат, если информация прямо противоположная, т. е. вероятность тумана — 0.7, а вероятность ясной погоды — 0.3. Тогда: Поезд W 1 = 16 ∙ 0.7 + 16 ∙ 0.3 =16 Самолет W 2 = 0 ∙ 0.3 + 26 ∙ 0.3=7.8 Автомобиль W 3 = 15 ∙ 0.7 + 19 ∙ 0.3=16.2 При таком вероятном прогнозе максимальная полезность достигается при третьем варианте, который означает выбор автомобиля. 5.5.3. «Максиминный» критерий Вальда. Предположим, что у нас нет никаких сведений о прогнозе на дни поездки, тогда все зависит от нашей точки зрения на ситуацию, от нашей позиции последствий какими грозит неудачный выбор решения. Примем в качестве критерия сравнения альтернатив критерий максимина:
Согласно этому критерию, оптимальным будем считать вариант, при котором гарантируется выигрыш не хуже, чем самый худший. Этот критерий олицетворяет «позицию крайнего пессимизма», надо всегда ориентироваться на худшие условия, зная наверняка, что «хуже этого не будет». Такой «перестраховочный» подход естественен для тех, кто очень боится проиграть. Конечно, он не является единственным, однако заслуживает рассмотрения. Чтобы применить данный критерий, необходимо в матрице полезностей в каждом столбце выбрать минимальное значение. Таблица 5.5.3.
Теперь, из полученных минимальных значений необходимо определить максимум — это будет 16. Данное значение полезности соответствует варианту выбора поезда.
5.5.4. Критерий минимаксного сожаления Сэвиджа. Этот критерий тоже крайне пессимистический, но при выборе оптимального варианта советует ориентироваться не на выигрыш, а на меньший проигрыш. Оптимальным считается тот вариант, для которого величина риска в наихудших условиях минимальна. Количественно риск
Для этого в каждой строке исходной матрицы находим максимальные значения. Таблица 5.5.4.
Из полученного максимального значения для каждого из возможных условий вычитаем исходные значения полезностей. Получаем преобразованную матрицу: Таблица 5.5.5.
Определяем максимальные значения для каждой строки (варианта) и из полученных величин выбираем минимальную.
При данных условиях S = 7, что соответствует варианту выбора автомобиля. Сущность такого подхода состоит в том, чтобы всячески избегать большого риска при принятии решения. В смысле «пессимизма» критерий Сэвиджа сходен с критерием Вальда, но «пессимизм» здесь понимается по-другому («выбирай наименьшую из потерь»). 5.5.5. Критерий пессимизма — оптимизма Гурвица. Этот критерий рекомендует при выборе решения не руководствоваться ни крайним пессимизмом («всегда рассчитывай на худшее!»), ни крайним, легкомысленным оптимизмом («авось кривая вывезет!»). Чтобы этим правилом воспользоваться, нужно ввести число к — коэффициент пессимизма и оптимизма в выборе решения. Если к — коэффициент пессимизма, то (1 — к) — коэффициент оптимизма. Примем к = 0.6, это значит, что вы умеренный пессимист, тогда коэффициент оптимизма будет (1 — к) = 0.4. Для каждого варианта, т. е. строки таблицы полезностей, находится наименьшее значение, и данные записываются в столбец минимумов. Этот столбец соответствует полностью оптимистическому взгляду на выигрыши. Аналогично формируется столбец максимумов, что соответствует пессимистическому взгляду на выигрыши. Результаты представлены в таблице: Таблица 5.5.6.
С учетом коэффициентов оптимизма и пессимизма рассчитываются оценки по данному критерию для каждого варианта:
где l Таблица 5.5.7.
Согласно критерию «пессимизма—оптимизма» выбирается вариант, удовлетворяющий максимальному значению, в нашем случае это H = 16.6, что соответствует варианту выбора автомобиля. Этот конкретный пример точно передает алгоритм процедуры, хотя для более яркой демонстрации результативности этих критериев желательно, чтобы число возможных вариантов условий прогноза было более двух. Контрольные вопросы 1. Определите и поясните на примере многокритериальную альтернативу. 2. Сформулируйте суть многокритериального выбора на примере деловой игры, приведенной в Приложении. 3. Сформулируйте цели по заданной вам проблеме и количественно определите приоритеты. 4. Определите основные способы сравнения альтернатив. 5. Сформулируйте принцип Парето и поясните на примере. 6. Определите сущность модели принятия решений Т. Бейеса. 7. В чем состоит специфика принятия решений в условиях неопределенности? 8. Назовите основные критерии, используемые в теории статистических решений.
Тема 6. КОЛЛЕКТИВНЫЕ РЕШЕНИЯ Сущность группового выбора Групповой выбор является столь же распространенным в практике принятия решений, как и индивидуальный. Под групповым выбором понимают процедуру принятия коллективного решения на основе согласования индивидуальных предпочтений членов группы. Этот факт был отмечен при формулировке задачи принятия решения в п. 2.2. Полное рассмотрение группового выбора предполагает решение проблем организации процедур выработки коллективного мнения и определение, что такое «хорошее», «разумное» согласование индивидуальных предпочтений в групповом предпочтении. Рациональная организация процедур выработки решения, т. е. технология работы группового ЛПР, требует учета поведения членов группы и влияния различных факторов на это поведение (характер решаемой проблемы, последовательность высказываемых мнений, условия образования коалиций, эмоциональное состояние участников и т. п.). Исследование поведения членов группового ЛПР является сложной проблемой. В теории принятия решений существуют работы, уделяющие особое внимание поведенческим и психологически аспектам коллективного выбора[45]. Но в данном пособии основное внимание уделяется проблемам рационального выбора. Основное направление исследований в области группового выбора связано не с тем, как должен проходить процесс выбора, а с тем, какими свойствами и требованиями должен обладать результат согласования индивидуальных предпочтений в групповое предпочтение. Такой подход, несмотря на свою неполноту за счет исключения поведенческого фактора, позволяет в широком аспекте подойти к проблеме группового выбора, включив в нее многокритериальный выбор, экспертные оценки, процедуры голосования и т. д. Конфликт предполагает принятие коллективного решения между субъектами, например, на этапе завершения, чтобы разрешить противоречие, положившее основу конфликту. Поэтому проблема коллективного выбора весьма актуальна для теоретических и практических аспектов конфликтологии.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 578; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.211.246 (0.011 с.) |

 , где l — номер альтернатив; j — номер варианта возможных условий.
, где l — номер альтернатив; j — номер варианта возможных условий. для каждого l -го варианта определим как разность между его полезностью и максимальным значением полезности среди всех вариантов, т. е.
для каждого l -го варианта определим как разность между его полезностью и максимальным значением полезности среди всех вариантов, т. е. 
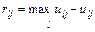 .
. , l — номер альтернативы; j — номер варианта возможных условий.
, l — номер альтернативы; j — номер варианта возможных условий.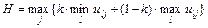 ,
, L — число альтернатив; j
L — число альтернатив; j 


