Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теория принятия статистических решенийСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
ТЕОРИЯ ПРИНЯТИЯ РЕШЕНИЙ Практикум
Владивосток Издательство ВГУЭС ВВЕДЕНИЕ.. 3
1. ТЕОРИЯ ПРИНЯТИЯ СТАТИСТИЧЕСКИХ РЕШЕНИЙ.. 4 1.1. Принятие решений при неизвестной априорной вероятности…...4 1.2. Максиминный критерий Вальда……………………………………5 1.3. Критерий минимакса сожалений Сэвиджа………………………..6 1.4. Критерий равновозможных состояний (Лапласа)………………...7 1.5. Критерий Гурвица…………………………………………………...8 1.6. Принятие решений при известных априорных вероятностях……………………………………………………………10 1.7. Задачи для самостоятельного решения…………………………..13
2. Многоэтапное принятие решений.. 18 2.1. Дерево решений…………………………………………………...18 2.2. Задачи для самостоятельного решения………………………….21
3. Нечеткие множества.. 26 3.1. Основные определения…………………………………………….26 3.2. Трапезоидные нечеткие числа…………………………………….28 3.3. Треугольные нечеткие числа. 29 3.4. Примеры задач по нечетким множествам.. 32 3.5. Метод анализа иерархий………………………………………….33 3.6. Задачи для самостоятельного решения…………………………..43
4. Оптимальный объем заказа.. 54 4.1. Модель оптимального объема заказа……………………………..54 4.2. Задачи для самостоятельного решения. 60
5. Системы массого обслуживания.. 67 5.1. Классификация систем массового обслуживания………………67 5.2. Расчеты характеристик СМО с помощью теории очередей……70 5.3. Задачи для самостоятельного решения…………………………..84 СПИСОК ЛИТЕРАТУРЫ... 92
Цель практикума – изложение принципиальных аспектов теории принятия решений, а также решение задач. Теоретический материал базируется на математических курсах по исследованию операций, математической статистике и включат в себя задачи принятия решений в условиях определенности, риска и неопределенности. В практикуме нашли отражение идеи, методы и результаты теории принятия решений, опубликованные в последние десятилетия в отечественной и зарубежной литературе; ряд примеров заимствован из этих источников. Следует иметь ввиду, что приведенные примеры экономических задач носят иллюстративный или даже схематический характер. Это объясняется тем, что для построения адекватных моделей реальных задач принятия решений в экономике требуется большой объем данных, сами задачи становятся весьма громоздкими; вместе с тем, проследить основные этапы анализа, логику рассуждений и применение математического аппарата гораздо легче на упрощенных моделях. В практикуме рассматриваются основы теории, на основе этой теории разбираются примеры, после чего даются примеры для самостоятельного решения. В основу настоящего пособия положен курс лекций, читаемый автором в Владивостокском Государственном Университете Экономики и Сервиса. Теория принятия статистических решений
Это чрезвычайно развитая область в экономике, в военном деле, в области обработки информации на фоне шумов и т. д. Рассмотрим элементы этой теории как продолжение теории игр. Принятие решений при неизвестной априорной Информации При рассмотрении критериев для принятия решений в условиях риска предполагается, что распределения вероятностей либо известны, либо могут быть найдены. Эти вероятности называются априорными вероятностями. Возьмем случай полной («дурной») неопределенности, когда вероятности состояний природы либо вообще не существуют, либо не поддаются оценке даже приближенно. Обстановка неблагоприятна для принятия «хорошего» решения — попытаемся найти хотя бы не самое худшее. Здесь все зависит от точки зрения на ситуацию, от позиции исследователя, от того, какими бедами грозит неудачный выбор решения. Опишем несколько возможных подходов, точек зрения (или, как говорят, несколько «критериев» для выбора решения). Пусть имеется совокупность действий, операций а1, а2,..., аm, m ³ 2, (1) которые может совершить человек для достижения поставленной цели, причем одну и только одну операцию аi, iÎ{1, 2,..., m}, выбирает человек, принимающий решение. Кроме того, представлен перечень объективных условий, например, состояний природы Q1, Q2,..., Qn, (2) одно из которых Qj, jÎ{1, 2,..., n}, будет иметь место в действительности. Для каждой операции аi, i = 1, 2,..., m, при любом условии Qj, j = 1, 2,..., n, задана полезность (выгода, доход) в некоторых единицах aij. Величины aij, играющие роль платежей в теории игр, обычно задаются из эвристических, субъективных соображений. При этом возникают специфические трудности при их числовой оценке, обусловленные такими факторами, как: болезни, удовольствия, престиж, репутация и т.д. Величины aij можно задавать относительно, поэтому их называют показателями предпочтительности. Все перечисленные условия, при которых принимается решение, представлены в табл. 1.
Таблица 1
Если ЛПР не располагает никакой информацией о состояниях природы (2), то имеем ситуацию принятия решения в условиях полной неопределенности. Рассмотрим четыре известных подхода ПР в этой ситуации.
1.2. Максиминный критерий Вальда. Согласно этому критерию игра с природой ведется как игра с разумным, причем агрессивным противником, делающим все для того, чтобы помешать нам достигнуть успеха. Оптимальной считается стратегия, при которой гарантируется выигрыш в любом случае не меньший, чем «нижняя цена игры с природой». Для каждой операции аi, i = 1, 2,..., m, находим наихудший исход,
Затем определяется то значение i0, при котором величина
Принимаемое решение – выбор наилучшей операции
Рассмотренная операция максимин соответствует лучшему из худших исходов. Если руководствоваться этим критерием, олицетворяющим «позицию, крайнего пессимизма», надо, всегда ориентироваться на худшие условия, зная наверняка, что «хуже этого не будет». Критерий максимина является чисто перестраховочным, поскольку природа не может быть сознательным противником. Очевидно, такой подход - естественный для того, кто очень боится проиграть, - не является единственно возможным, но как крайний случай он заслуживает рассмотрения. Максиминную операцию использует только крайний пессимист, не желающий идти ни на какой риск. Обычно такие люди довольствуются малым и предпочитают спокойную жизнь.
1.3.Критерий минимакса сожалений Сэвиджа Этот критерий — тоже крайне пессимистический, но при выборе оптимальной стратегии советует ориентироваться не на выигрыш, а на риск. Выбирается в качестве оптимальной та стратегия, при которой величина риска (сожаления) в наихудших условиях минимальна. Сожаление (риска) в ТПР – потери в результате упущенных возможностей. Пусть природа находится в состоянии Qs найдем максимальный элемент s-го столбца табл. 1,
Мера сожаления определяется как разность:
где Для принятия решения к табл. 2 применяется критерий минимакса (minmax): для каждой операции ai, i=1,2,…, m, находится наибольшее сожаление,
Таблица 2
Затем среди членов последовательности
Последние два равенства соединим в одно:
Принимаемое решение – наилучшая операция Сущность такого подхода в том, чтобы всячески избегать большого риска при принятии решения. В смысле «пессимизма» критерий Сэвиджа сходен с критерием Вальда, но самый «пессимизм» здесь понимается по-другому.
1.4 Критерий равновозможных состояний (Лапласа) По этому критерию выбирается та операция ai0, для которой сумма полезностей
максимальна,
Задача. Рассмотрим на конкретном примере принятие решений по трем описанным критериям. Пусть m=3, n=2, и матрица полезностей представлена в табл. 3.
Таблица 3
Таблица 4
Например, ai – i-ый вариант технологического процесса для изготовления некоторых изделий, Q1 – возникновение дефицита в ближайшие два года на сырье, из которого изготовляются детали, Q2 – отсутствие такого дефицита. 1. Применяя операцию максимина, получим
Максиминной операцией является операция а2, гарантирующая 6 единиц полезности.
2. Для использования критерия минимакса сожалений необходимо для данных табл. 3 найти матрицу сожалений. Сначала находим максимальный элемент каждого столбца этой таблицы:
Тогда матрица сожалений примет вид, представленный в табл. 4. Применяя к данным этой таблицы критерий минимакса, получим: max(9, 3) = 9, max(0, 8) = 8, max(10, 0) = 10, min(9, 8, 10) = 8. Следовательно, операцией, соответствующей минимаксу сожалений, является операция а2. По критерию равновозможных состояний для данных табл. 3 имеем: Аi = 1+11 = 12, A2 = 10+6 = 16, A3 = 0+14 = 14,
Значит, оптимальной операцией по критерию равновозможных состояний природы является операция а2. В рассмотренном примере все три критерия дали один и тот же ответ: операция а2 является оптимальной, она гарантирует 6 ед. полезности. Если выбрать операцию а1, то в случае везения получим 11 ед. полезности, а в случае невезения – всего 1 ед. полезности. Если выбрать операцию а3, то в случае везения имеем 14 ед. полезности, а в случае невезения – 0 ед. полезности. Операция а2 гарантирует наибольшую полезность, 6 ед. Конкурирующие операции а1 и а3 гарантируют меньшие полезности: 1 ед. и 0 ед., соответственно.
Критерий Гурвица Этот критерий охватывает ряд различных подходов к принятию решений: от наиболее оптимистичного до наиболее пессимистичного. При наиболее оптимистичном подходе можно выбрать действие, дающее maxai maxq j { v(ai, q j) }. (Предполагается, что v(ai, q j) представляет выигрыш, или доход.) Аналогично при наиболее пессимистичных предположениях выбираемое действие соответствует maxai minq j { v(ai, q j) }. Критерий Гурвица устанавливает баланс между случаями крайнего оптимизма и крайнего пессимизма взвешиванием обоих способов поведения с соответствующими весами a и 1-a, где 0£a£1. Если v(ai, q j) представляет прибыль, то выбирается действие, дающее maxai {a maxq j v(ai, q j) + (1-a)minq j { v(ai, q j) }.В том случае, когда представляются затраты, критерий выбирает действие, дающее minai {a minq j v(ai, q j) + (1-a)maxq j { v(ai, q j) }.Параметр
ПРИМЕР: Одно из предприятий должно определить уровень предложенных услуг так, чтобы удовлетворить потребности клиентов в течении предстоящих праздников. Точное число клиентов не известно, но ожидается, что оно может принимать одно из четырех значений: 200, 250, 300 или 350 клиентов. Для каждого из этих возможных значений существует наилучший уровень предложения (с точки зрения возможных затрат). Отклонения от этих уровней приводят к дополнительным затратам либо из-за превышения предложения над спросом, либо из-за неполного удовлетворения спроса. Приводится таблица, определяющая потери в тысячах $.
Положим ниже. Оптимальное решение заключается в выборе
Вероятностях. Самый простой случай неопределенности — т.н. «доброкачественная» или стохастическая неопределенность, когда состояния природы имеют какие-то вероятности. Тогда естественно выбрать ту стратегию, для которой среднее значение выигрыша, взятое по строке, максимально. Ситуация ПР в условиях риска возникает в случаях, когда известны априорные вероятности состояний природы р(Q1), р(Q2), …, р(Qn),
Естественно воспользоваться этой дополнительной информацией. С этой целью для каждой операции аi находят взвешенные суммы полезностей
и выбирают в качестве наилучшей ту операцию
Любопытно отметить, что та же стратегия, которая обращает в максимум средний выигрыш, обращает в минимум в средний риск. Так что в случае стохастической неопределенности оба подхода («от выигрыша» и «от риска») дают одно В то же оптимальное решение. Пусть в рассмотренном выше примере р(Q1)=0.25, р(Q2)=0.75. По данным табл. 3 имеем
max (8.5; 7.0; 10.5) = 10.5. Следовательно, наилучшей операцией является операция а3, если р(Q1)=0.25, р(Q2)=0.75. Но при других значениях априорных вероятностей состояний природы возможен и другой выбор. Используя данные табл.3 и формулу (6) для каждой операции аi, i = 1,2,3, имеем
На рис.А даны графики функций
Прямые  , ,  пересекаются в точке В, при пересекаются в точке В, при  , вычисленного из равенства 6 + 4р = 14 – 14р. Из рис. А следует, что при , вычисленного из равенства 6 + 4р = 14 – 14р. Из рис. А следует, что при  лучшей операцией является а3, а при лучшей операцией является а3, а при  лучшей операцией является а2. лучшей операцией является а2.
При Если р=0 или 1, то имеем ситуацию ПР в условиях достоверности. При р=0 лучшая операция – а3, при р=1 лучшая операция – а2.
1.7. Задания для самостоятельного решения
Вариант 1 Предприятие производит электротермометры ЭТ-2000, которые c вероятностью p могут быть дефектными. Количество изделий в партии 200. Прошлый опыт указывает, что из-за неустойчивой работы производственной линии p равно либо 0.05, либо 0.10, либо 0.25. Причем, в 70 % произведенных партий, p равняется 0.05, в 20% - p= 0.10, а в 10% партий p равняется 0.25. ЭТ-2000 используются при сборке приборов, и в конечном счете их качество будет определено конечным ОТК. При этом можно или испытывать каждый электротермометр на специальном стенде, что обходится в $8 за штуку и отбрасывать дефектные или использовать его на сборке непосредственно без испытания. Если выбрано последнее, дефект обнаружится при сплошном оконечном контроле, а стоимость переделки составит в конечном счете $90 за каждый прибор. a. По этим данным постройте матрицу прибылей и рассчитайте ожидаемые затраты на каждую партию. Какое решение следует принять, испытывать электротермометры или нет? b. Допустим, что из каждой партии можно отправить в лабораторию 10 термометров, и по этой выборке достоверно установить процент бракованных изделий в партии. Стоимость анализа $200. Стоит ли проводить такой анализ? Каковы будут суммарные издержки в этом случае?
Вариант 2 Годовой запас ботинок некоторого популярного типа для большого универмага нужно заказывать заранее. Каждая пара стоит $ 30, продается за $ 60, и может быть продана на распродаже только за $ 15, если не будет продана до конца года. Рассматриваются следующие варианты заказа: 20, 30, 40 или 50 пар. Уровни спроса и их вероятности даны в таблице:
Сформируйте матрицу прибылей (выигрышей) и матрицу упущенных возможностей (рисков). Сколько пар ботинок нужно заказывать, чтобы максимизировать ожидаемую прибыль? Используйте критерии максимина, минимаксного риска и максимума ожидаемой прибыли для принятия решения о величине заказа.
Вариант 3 Маленькая кондитерская в курортном городе продает выпечку собственного производства. Фирменные торты выпекаются каждое утро и продаются по цене 210 рублей (при себестоимости – 90 рублей). Если торт не продается в день изготовления, он выбрасывается. Записи, которые ведет хозяйка, показывают, что за последние 100 дней спрос на эти торты имел следующее распределение.
Используйте критерии максимина, минимаксного риска и максимума ожидаемой прибыли для принятия решения о партии тортов.
Вариант 4 Менеджер закупочного отдела магазина хозяйственных товаров должен решить сколько циркулярных пил закупить для продажи в текущем строительном сезоне. Каждая пила покупается у дилера за 1800 рублей, а продается в магазине за 3000 рублей. Каждая непроданная в сезон пила требует серьезных расходов на хранение и в результате приносит убыток 750 рублей. Менеджер может покупать товар у дилера только партиями по 100 штук. Из прошлого опыта известны вероятности продать партии товара различного размера.
Сформируйте матрицу прибылей (выигрышей) и матрицу упущенных возможностей (рисков). Используйте критерии максимина, минимаксного риска и максимума ожидаемой прибыли для принятия решения о величине заказа циркулярных пил. Какова будет средняя прибыль при каждом из выборов партии?
Вариант 5 Виктор - прилежный студент, получающий хорошие отметки благодаря, в частности тому, что имеет возможность повторить материал в ночь перед экзаменом. Перед завтрашним экзаменом Виктор столкнулся с тем, что его сокурсники организовали вечеринку, в которой он не хочет участвовать. Виктор имеет три альтернативы: А1 – участвовать в вечеринке всю ночь. А2 – половину ночи участвовать, а половину учиться, А3 – учиться всю ночь. Профессор, принимающий экзамен, непредсказуем в том смысле, что экзамен может быть легким (S1), средним (S2) или трудным (S2). Можно ожидать следующие экзаменационные балы:
Найти выигрышные стратегии с использованием критерия Вальда, критерия Сэвиджа, критерия Гурвица (3 разных варианта показателя оптимизма), критерия Лапласа. Сформулировать собственную рекомендацию Виктору.
Вариант 6 В приближении посевного сезона фермер имеет четыре альтернативы: А1 – выращивать кукурузу, А2 – выращивать пшеницу, А3 – выращивать соевые бобы, А4 – использовать землю пот пастбища. Платежи, связанные с указанными возможностями. Зависят от количества осадков, которые можно разделить на следующие категории: S1 – сильные осадки, S2 – умеренные осадки, S3 – незначительные осадки, S4 – засушливый сезон. Платежная матрица оценивается следующим образом
Найти выигрышные стратегии с использованием критерия Вальда, критерия Сэвиджа, критерия Гурвица (3 разных варианта показателя оптимизма), критерия Лапласа. Сформулировать собственную рекомендацию фермеру.
Вариант 7 Один из N станков должен быть выбран для изготовления Q единиц определенно продукции. Минимальная и максимальная потребность в продукции равна Q* и Q** соответственно. Производственные затраты ТСi на изготовление Q единиц продукции на станке i включает фиксированные затраты Кi и удельные затраты сi на производство единицы продукции и выражаются формулой ТСi = Кi + сi Q. Решить задачу при следующих данных:
Найти выигрышные стратегии с использованием критерия Вальда, критерия Сэвиджа, критерия Гурвица (3 разных варианта показателя оптимизма), критерия Лапласа. Сформулировать собственную рекомендацию. Вариант 8 Одно из предприятий должно определить уровень предложения услуг так, чтобы удовлетворить потребности клиентов в течении предстоящих праздников. Точное число клиентов неизвестно, но ожидается, что оно может принимать одно из четырех значений: 200, 250, 300, 350 клиентов. Для каждого из этих возможных значений существует наилучший уровень предложения (с точки зрения наилучших затрат). Отклонения от этих уровней приводят к дополнительным затратам либо из-за превышения, либо из-за неполного удовлетворения спроса. Ниже приводится таблица, определяющая потери в тыс. рублей.
Найти выигрышные стратегии с использованием критерия принятия решения. Сформулировать собственную рекомендацию.
Вариант 9 Национальная школа выживания подбирает место для строительства летнего лагеря в центре Аляски. Число участников сбора может быть: 200, 250, 300, 350. Стоимость проживания будет минимальной, поскольку он строится для удовлетворения небольших потребностей. Отклонения в сторону уменьшения или увеличения относительно идеальных уровней, влекут за собой дополнительные затраты (в силу избытка мест или потерь возможности получить прибыль). А1-А4 представляют размеры лагеря (в кол-ве мест), а S1-S4 число участников сбора. Ниже представлена матрица, описывающая ситуацию.
Проанализировать ситуацию с точки зрения всех критериев. Вариант 10 Предприниматель решает проблему – какого размера строить предприятие: маленькое предприятие, среднее, крупное. От маленького предприниматель ожидает прибыль 100 тыс. долл. при плохом спросе, 150 – при среднем, 200 – при хорошем. От среднего предприятия ожидается 180 тыс. при плохом спросе, 250 тыс. – при среднем, 300 – при хорошем. От крупного предприятия ожидается 200 тыс. при плохом спросе, 280 тыс. – при среднем, 350 – при хорошем. Найти выигрышные стратегии с использованием критерия Вальда, критерия Сэвиджа, критерия Гурвица (3 разных варианта показателя оптимизма), критерия Лапласа. Сформулировать собственную рекомендацию.
Дерево решений
Многоэтапность приводит к тому, что схема принятия решения может быть представлена в виде дерева, в каждой вершине которого осуществляется либо: 1) Сознательный выбор между двумя и более альтернативами 2) Случайный переход из одной ветви в другую под воздействием внешних факторов Рассмотрим пример оптимизации многоэтапных решений на примере экономической задачи. Пример. Фирма может принять решение о строительстве крупного или мелкого предприятия. Строительство крупного предприятия относительно дешевле, в случае если будет высокий спрос на производимые товары, мелкое предприятие можно расширить. Деятельность фирмы рассматривается в течение десяти лет, причём в случае строительства мелкого предприятия, вопрос о расширении будет рассматриваться через два года. Спрос заранее неизвестен. Решение. Введём градацию спроса: высокий Расширенное предприятие в случае высокого спроса приносит доход – 900 тыс. $ в год, и при низком спросе – 200 тыс. $; мелкое предприятие без расширения при высоком спросе на производимый продукт приносит в течение двух лет по 250 тыс. $ ежегодно, а в течение следующих восьми по 200 тыс. $. Нарисуем наше дерево.
Применим для решения этой задачи метод динамического программирования. В качестве критерия применим средний выигрыш, т.е. МО выигрыша. Сама величина критерия равна доходу без затрат на строительство. Начнём с последнего четвёртого шага: подсчитаем средний выигрыш:
В данной задаче мы должны сделать два осознанных выбора. В первом случае мы видим, что выгодней не расширять мелкое предприятие через 2 года работы, в этом случае средний выигрыш будет выше на 300 тыс. Если выбирать между строительством крупного или мелкого предприятия, то оптимальным будем сразу строить крупное предприятие, в этом случае средний выигрыш составит 3,25 млн, тогда как при строительстве мелкого предприятия – 1,3 млн.
Вариант 1 Вас пригласили на телевизионную игру Колесо фортуны. Колесо управляется электронным образом с помощью двух кнопок, которые сообщают колесу сильное (В) или слабое (Н) вращение. Само колесо разделено на равные области – белую (Б) и красную (К). Вам сообщили, что в белой части колесо останавливается с вероятностью 0,3, а в красной – 0,7. Плата, которую вы получаете за игру, равна (в рублях) следующему.
Изобразите соответствующее дерево решений. Вариант 2 Фермер Василий может выращивать либо кукурузу, либо соевые бобы. Вероятность того, что цены на будущий урожай этих культур повысятся, останутся на том же уровне или понизятся, равна соответственно 0.25, 0.30 и 0.45. Если цены возрастут, урожай кукурузы даст 3000000 рублей чистого дохода, а урожай соевых бобов – 1000000 рублей. Если цены останутся неизменными, Василий лишь покроет расходы. Но если цены станут ниже, урожай кукурузы и соевых бобов приведет к потерям в 2500000 и 500000 рублей соответственно. а) Представьте данную задачу в виде дерева решений. b) Какую культуру следует выращивать Василию?
Вариант 3 Допустим, у вас имеется возможность вложить деньги в три инвестиционных фонда открытого типа: простой, специальный (обеспечивающий максимальную долгосрочную прибыль от акций мелких компаний) и глобальный. Прибыль от инвестиции может измениться в зависимости от условий рынка. Существует 10%-ная вероятность, что ситуация на рынке ценных бумаг ухудшится, 50%-ная – что рынок останется умеренным и 40%-ная – рынок будет возрастать. Следующая таблица содержит значения процентов прибыли от суммы инвестиции при трех возможностях развития рынка.
а) Представьте задачу в виде дерева решений. b) Какой фонд открытого типа вам следует выбрать?
Вариант 4 Предположим, у вас имеется возможность вложить деньги в 7.5%-ные облигации, которые продаются по номинальной цене, либо в специальный фонд, который выплачивает лишь 1% дивидендов. Если существует вероятность инфляции, процентная ставка возрастет до 8%, и в этом случае номинальная стоимость облигаций увеличится на 10%, а цена акций фонда – на 20%. Если прогнозируется спад, то процентная ставка понизится до 6%. При этих условиях ожидается, что номинальная стоимость облигаций поднимется на 5%, а цена акций фонда увеличится на 20%. Если состояние экономики останется неизменным, цена акций фонда увеличится на 8%, а номинальная стоимость облигаций не изменится. Экономисты оценивают в 20% шансы наступления инфляции и в 15% - наступление спада. Ваше решение относительно инвестиций принимается с учётом экономических условий следующего года. а) Представьте задачу в виде дерева решений. b) Будете ли вы покупать акции фонда или облигации?
Вариант 5 Фирма планирует производство новой продукции питания. Исследовательский отдел убеждён в большом успехе новой продукции и хочет внедрить ее немедленно, без рекламной кампании на рынках сбыта фирма. Отдел маркетинга положение вещей оценивает иначе и предлагает провести интенсивную рекламную кампанию. Такая кампания обойдётся в 1 млн. рублей, а в случае успеха принесет 9,5 млн. рублей годового дохода. В случае неуспеха рекламной кампании (вероятность этого составляет 30%) годовой доход оценивается лишь в 2 млн. рублей. Если рекламная кампания не проводится вовсе, годовой доход оценивается в 4 млн. рублей при условии, что покупателям понравится новая продукция (вероятность этого равна 0.8), и в 2 млн. рублей с вероятностью 0.2, если покупатели останутся равнодушными к новой продукции. а) Постройте соответствующее дерево решений. b) Как должна поступить фирма в связи с производством новой продукции?
Вариант 6 Симметричная монета подбрасывается три раза. Вы получаете один рубль за каждое выпадение герба (Г) и дополнительно 25 копеек за каждые два последовательных выпадения герба (заметим, что выпадение ГГГ состоит из двух последовательностей ГГ). Однако Вам приходится платить 1.1 рубля за каждое выпадение решетки (Р). Вашим решением является участие или неучастие в игре. а) Постройте соответствующее дерево решений для описанной игры. b) Будете ли вы играть в
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1571; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.171.43 (0.227 с.) |

 . (3а)
. (3а) максимальна,
максимальна, . (3в)
. (3в) из множества исходных (1). Равенства (3а), (3в) можно объединить в одно
из множества исходных (1). Равенства (3а), (3в) можно объединить в одно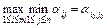 . (4)
. (4) .
.
 если
если  если
если  Тогда при состоянии природы Qs лучшей операцией является
Тогда при состоянии природы Qs лучшей операцией является  : для нее сожаление равно нулю. Изменяя последовательно значения s, s = 1,2,…, n, получим сожаление для каждой операции ai, i=1,2,…, m, при любом состояния природы Qs, s=1,2,…, n. Матрица сожалений представлена в табл. 2.
: для нее сожаление равно нулю. Изменяя последовательно значения s, s = 1,2,…, n, получим сожаление для каждой операции ai, i=1,2,…, m, при любом состояния природы Qs, s=1,2,…, n. Матрица сожалений представлена в табл. 2.
 , i=1,2,…, m, s = 1,2,…, n, находится минимальный
, i=1,2,…, m, s = 1,2,…, n, находится минимальный



 .
.



 .
. определяется как показатель оптимизма: при
определяется как показатель оптимизма: при 











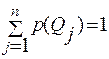 . (5)
. (5) i=1,2, …, m, (6)
i=1,2, …, m, (6) , для которой взвешенная сумма полезностей в (6) максимальна,
, для которой взвешенная сумма полезностей в (6) максимальна,
 = 1×0.25 + 11×0.75 = 8.5,
= 1×0.25 + 11×0.75 = 8.5, = р +11(1– p) = 11 – 10p,
= р +11(1– p) = 11 – 10p,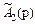 = 10p +6(1 – p) = 6 + 4p,
= 10p +6(1 – p) = 6 + 4p,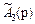 = 14(1 – p) = 14 – 14p.
= 14(1 – p) = 14 – 14p. , i= 1, 2, 3.
, i= 1, 2, 3.
 безразлично, какую операцию а2 или а3 использовать. Операцию а1 применять невыгодно.
безразлично, какую операцию а2 или а3 использовать. Операцию а1 применять невыгодно.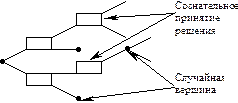
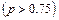 и низкий
и низкий 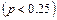 . Затраты и доходы: строительство крупного предприятия – 5 млн. $; строительство мелкого – 1 млн. $; затраты на расширение – 4,2 млн. $; крупное предприятие при высоком спросе даёт доход – 1 млн. $ ежегодно, а при низком – 300 тыс. $; мелкое предприятие при высоком спросе – 250 тыс. $ ежегодно, при низком – 200 тыс. $.
. Затраты и доходы: строительство крупного предприятия – 5 млн. $; строительство мелкого – 1 млн. $; затраты на расширение – 4,2 млн. $; крупное предприятие при высоком спросе даёт доход – 1 млн. $ ежегодно, а при низком – 300 тыс. $; мелкое предприятие при высоком спросе – 250 тыс. $ ежегодно, при низком – 200 тыс. $.