
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принятие решений при известных априорныхСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Вероятностях. Самый простой случай неопределенности — т.н. «доброкачественная» или стохастическая неопределенность, когда состояния природы имеют какие-то вероятности. Тогда естественно выбрать ту стратегию, для которой среднее значение выигрыша, взятое по строке, максимально. Ситуация ПР в условиях риска возникает в случаях, когда известны априорные вероятности состояний природы р(Q1), р(Q2), …, р(Qn),
Естественно воспользоваться этой дополнительной информацией. С этой целью для каждой операции аi находят взвешенные суммы полезностей
и выбирают в качестве наилучшей ту операцию
Любопытно отметить, что та же стратегия, которая обращает в максимум средний выигрыш, обращает в минимум в средний риск. Так что в случае стохастической неопределенности оба подхода («от выигрыша» и «от риска») дают одно В то же оптимальное решение. Пусть в рассмотренном выше примере р(Q1)=0.25, р(Q2)=0.75. По данным табл. 3 имеем
max (8.5; 7.0; 10.5) = 10.5. Следовательно, наилучшей операцией является операция а3, если р(Q1)=0.25, р(Q2)=0.75. Но при других значениях априорных вероятностей состояний природы возможен и другой выбор. Используя данные табл.3 и формулу (6) для каждой операции аi, i = 1,2,3, имеем
На рис.А даны графики функций
Прямые  , ,  пересекаются в точке В, при пересекаются в точке В, при  , вычисленного из равенства 6 + 4р = 14 – 14р. Из рис. А следует, что при , вычисленного из равенства 6 + 4р = 14 – 14р. Из рис. А следует, что при  лучшей операцией является а3, а при лучшей операцией является а3, а при  лучшей операцией является а2. лучшей операцией является а2.
При Если р=0 или 1, то имеем ситуацию ПР в условиях достоверности. При р=0 лучшая операция – а3, при р=1 лучшая операция – а2.
1.7. Задания для самостоятельного решения
Вариант 1 Предприятие производит электротермометры ЭТ-2000, которые c вероятностью p могут быть дефектными. Количество изделий в партии 200. Прошлый опыт указывает, что из-за неустойчивой работы производственной линии p равно либо 0.05, либо 0.10, либо 0.25. Причем, в 70 % произведенных партий, p равняется 0.05, в 20% - p= 0.10, а в 10% партий p равняется 0.25. ЭТ-2000 используются при сборке приборов, и в конечном счете их качество будет определено конечным ОТК. При этом можно или испытывать каждый электротермометр на специальном стенде, что обходится в $8 за штуку и отбрасывать дефектные или использовать его на сборке непосредственно без испытания. Если выбрано последнее, дефект обнаружится при сплошном оконечном контроле, а стоимость переделки составит в конечном счете $90 за каждый прибор. a. По этим данным постройте матрицу прибылей и рассчитайте ожидаемые затраты на каждую партию. Какое решение следует принять, испытывать электротермометры или нет? b. Допустим, что из каждой партии можно отправить в лабораторию 10 термометров, и по этой выборке достоверно установить процент бракованных изделий в партии. Стоимость анализа $200. Стоит ли проводить такой анализ? Каковы будут суммарные издержки в этом случае?
Вариант 2 Годовой запас ботинок некоторого популярного типа для большого универмага нужно заказывать заранее. Каждая пара стоит $ 30, продается за $ 60, и может быть продана на распродаже только за $ 15, если не будет продана до конца года. Рассматриваются следующие варианты заказа: 20, 30, 40 или 50 пар. Уровни спроса и их вероятности даны в таблице:
Сформируйте матрицу прибылей (выигрышей) и матрицу упущенных возможностей (рисков). Сколько пар ботинок нужно заказывать, чтобы максимизировать ожидаемую прибыль? Используйте критерии максимина, минимаксного риска и максимума ожидаемой прибыли для принятия решения о величине заказа.
Вариант 3 Маленькая кондитерская в курортном городе продает выпечку собственного производства. Фирменные торты выпекаются каждое утро и продаются по цене 210 рублей (при себестоимости – 90 рублей). Если торт не продается в день изготовления, он выбрасывается. Записи, которые ведет хозяйка, показывают, что за последние 100 дней спрос на эти торты имел следующее распределение.
Используйте критерии максимина, минимаксного риска и максимума ожидаемой прибыли для принятия решения о партии тортов.
Вариант 4 Менеджер закупочного отдела магазина хозяйственных товаров должен решить сколько циркулярных пил закупить для продажи в текущем строительном сезоне. Каждая пила покупается у дилера за 1800 рублей, а продается в магазине за 3000 рублей. Каждая непроданная в сезон пила требует серьезных расходов на хранение и в результате приносит убыток 750 рублей. Менеджер может покупать товар у дилера только партиями по 100 штук. Из прошлого опыта известны вероятности продать партии товара различного размера.
Сформируйте матрицу прибылей (выигрышей) и матрицу упущенных возможностей (рисков). Используйте критерии максимина, минимаксного риска и максимума ожидаемой прибыли для принятия решения о величине заказа циркулярных пил. Какова будет средняя прибыль при каждом из выборов партии?
Вариант 5 Виктор - прилежный студент, получающий хорошие отметки благодаря, в частности тому, что имеет возможность повторить материал в ночь перед экзаменом. Перед завтрашним экзаменом Виктор столкнулся с тем, что его сокурсники организовали вечеринку, в которой он не хочет участвовать. Виктор имеет три альтернативы: А1 – участвовать в вечеринке всю ночь. А2 – половину ночи участвовать, а половину учиться, А3 – учиться всю ночь. Профессор, принимающий экзамен, непредсказуем в том смысле, что экзамен может быть легким (S1), средним (S2) или трудным (S2). Можно ожидать следующие экзаменационные балы:
Найти выигрышные стратегии с использованием критерия Вальда, критерия Сэвиджа, критерия Гурвица (3 разных варианта показателя оптимизма), критерия Лапласа. Сформулировать собственную рекомендацию Виктору.
Вариант 6 В приближении посевного сезона фермер имеет четыре альтернативы: А1 – выращивать кукурузу, А2 – выращивать пшеницу, А3 – выращивать соевые бобы, А4 – использовать землю пот пастбища. Платежи, связанные с указанными возможностями. Зависят от количества осадков, которые можно разделить на следующие категории: S1 – сильные осадки, S2 – умеренные осадки, S3 – незначительные осадки, S4 – засушливый сезон. Платежная матрица оценивается следующим образом
Найти выигрышные стратегии с использованием критерия Вальда, критерия Сэвиджа, критерия Гурвица (3 разных варианта показателя оптимизма), критерия Лапласа. Сформулировать собственную рекомендацию фермеру.
Вариант 7 Один из N станков должен быть выбран для изготовления Q единиц определенно продукции. Минимальная и максимальная потребность в продукции равна Q* и Q** соответственно. Производственные затраты ТСi на изготовление Q единиц продукции на станке i включает фиксированные затраты Кi и удельные затраты сi на производство единицы продукции и выражаются формулой ТСi = Кi + сi Q. Решить задачу при следующих данных:
Найти выигрышные стратегии с использованием критерия Вальда, критерия Сэвиджа, критерия Гурвица (3 разных варианта показателя оптимизма), критерия Лапласа. Сформулировать собственную рекомендацию. Вариант 8 Одно из предприятий должно определить уровень предложения услуг так, чтобы удовлетворить потребности клиентов в течении предстоящих праздников. Точное число клиентов неизвестно, но ожидается, что оно может принимать одно из четырех значений: 200, 250, 300, 350 клиентов. Для каждого из этих возможных значений существует наилучший уровень предложения (с точки зрения наилучших затрат). Отклонения от этих уровней приводят к дополнительным затратам либо из-за превышения, либо из-за неполного удовлетворения спроса. Ниже приводится таблица, определяющая потери в тыс. рублей.
Найти выигрышные стратегии с использованием критерия принятия решения. Сформулировать собственную рекомендацию.
Вариант 9 Национальная школа выживания подбирает место для строительства летнего лагеря в центре Аляски. Число участников сбора может быть: 200, 250, 300, 350. Стоимость проживания будет минимальной, поскольку он строится для удовлетворения небольших потребностей. Отклонения в сторону уменьшения или увеличения относительно идеальных уровней, влекут за собой дополнительные затраты (в силу избытка мест или потерь возможности получить прибыль). А1-А4 представляют размеры лагеря (в кол-ве мест), а S1-S4 число участников сбора. Ниже представлена матрица, описывающая ситуацию.
Проанализировать ситуацию с точки зрения всех критериев. Вариант 10 Предприниматель решает проблему – какого размера строить предприятие: маленькое предприятие, среднее, крупное. От маленького предприниматель ожидает прибыль 100 тыс. долл. при плохом спросе, 150 – при среднем, 200 – при хорошем. От среднего предприятия ожидается 180 тыс. при плохом спросе, 250 тыс. – при среднем, 300 – при хорошем. От крупного предприятия ожидается 200 тыс. при плохом спросе, 280 тыс. – при среднем, 350 – при хорошем. Найти выигрышные стратегии с использованием критерия Вальда, критерия Сэвиджа, критерия Гурвица (3 разных варианта показателя оптимизма), критерия Лапласа. Сформулировать собственную рекомендацию.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1049; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.241.235 (0.007 с.) |

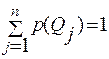 . (5)
. (5) i=1,2, …, m, (6)
i=1,2, …, m, (6) , для которой взвешенная сумма полезностей в (6) максимальна,
, для которой взвешенная сумма полезностей в (6) максимальна,
 = 1×0.25 + 11×0.75 = 8.5,
= 1×0.25 + 11×0.75 = 8.5, = р +11(1– p) = 11 – 10p,
= р +11(1– p) = 11 – 10p,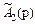 = 10p +6(1 – p) = 6 + 4p,
= 10p +6(1 – p) = 6 + 4p,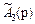 = 14(1 – p) = 14 – 14p.
= 14(1 – p) = 14 – 14p. , i= 1, 2, 3.
, i= 1, 2, 3.
 безразлично, какую операцию а2 или а3 использовать. Операцию а1 применять невыгодно.
безразлично, какую операцию а2 или а3 использовать. Операцию а1 применять невыгодно.


