
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Операции над нечеткими числамиСодержание книги Поиск на нашем сайте
Целый раздел теории нечетких множеств – мягкие вычисления (нечеткая арифметика) - вводит набор операций над нечеткими числами. Эти операции вводятся через операции над функциями принадлежности на основе так называемого сегментного принципа. Определим уровень принадлежности a как ординату функции принадлежности нечеткого числа. Тогда пересечение функции принадлежности с нечетким числом дает пару значений, которые принято называть границами интервала достоверности. Зададимся фиксированным уровнем принадлежности a и определим соответствующие ему интервалы достоверности по двум нечетким числам
· операция "сложения":
[a1, a2] (+) [b1, b2] = [a1 + b1, a2 + b2], (2)
· операция "вычитания":
[a1, a2] (-) [b1, b2] = [a1 - b2, a2 - b1], (3)
· операция "умножения":
[a1, a2] (´) [b1, b2] = [a1 ´ b1, a2 ´ b2], (4)
· операция "деления":
[a1, a2] (/) [b1, b2] = [a1 / b2, a2 / b1], (5)
· операция "возведения в степень":
[a1, a2] (^) i = [a1i, a2i]. (6)
Из существа операций с трапезоидными числами можно сделать ряд важных утверждений (без доказательства): · действительное число есть частный случай треугольного нечеткого числа; · сумма треугольных чисел есть треугольное число; · треугольное (трапезоидное) число, умноженное на действительное число, есть треугольное (трапезоидное) число; · сумма трапезоидных чисел есть трапезоидное число; · сумма треугольного и трапезоидного чисел есть трапезоидное число. Анализируя свойства нелинейных операций с нечеткими числами (например, деления), исследователи приходят к выводу, что форма функций принадлежности результирующих нечетких чисел часто близка к треугольной. Это позволяет аппроксимировать результат, приводя его к треугольному виду. И, если приводимость налицо, тогда операции с треугольными числами сводятся к операциям с абсциссами вершин их функций принадлежности. То есть, если мы вводим описание треугольного числа набором абсцисс вершин (a, b, c), то можно записать: (a1, b1, c1) + (a2, b2, c2) º (a1 + a2, b1 + b2, c1 + c2) (7)
Это – самое распространенное правило мягких вычислений.
Примеры задач по нечетким множествам.
Вариант 1 Найдите сумму, разность, произведение, частное двух нечетких треугольных чисел A=(1,4,6), B=(3,6,9).
Вариант 2. Решить уравнение (А-В)*х3 = С. А = (4,7,9), В=(2,2,5,8), С=(2,4,7).
Вариант 3. Найдите сумму, разность, произведение, частное треугольного числа A=(3,6,7) и трапезоидного числа B=(1,3,5,11).
Вариант 4. Задать нечеткое множество соответствующее терму: «люди среднего возраста» и «не студенты». Построить график этой функции принадлежности.
Вариант 5. Задать нечеткое множество соответствующее терму: «число очень близкое к 2» и «далекое от 5». Построить график этой функции принадлежности.
Вариант 6. Решить уравнение (А+В)*х2 = С. А = (1,3,4), В=(2,2,5,8), С=(2,4,7).
Вариант 7. Задать нечеткое множество соответствующее терму: «заработок близкий к 10 т.р.» и «заработок далекий от прожиточного минимума». Построить график этой функции принадлежности
Вариант 8. Задать нечеткое множество соответствующее терму: «число достаточно близкое к 4» и «далекое от 10». Построить график этой функции принадлежности.
Метод анализа иерархий
Оценку вариантов решений методом анализа иерархий покажем на иллюстративном примере «Переправа через реку». 1. Требуется определить: оставить на реке паромную переправу или вместо нее построить мост или туннель. 2. Возможные решения оцениваются по трем критериям: экономическому, социальному, и экологическому. Каждый критерий оценивается по критериям низкого уровня. 3. Структурный граф процесса принятия решения с указанием уровня иерархий и оценками + и -, указывающими, способствует или препятствует данный фактор решению задачи, показан на рис.1 Возможные варианты решений определены в постановке задачи. 4. Значения критериев первого уровня показаны в табл. 1.а и 1.б.
Таблица 1.a
Таблица 1.b
Не будем обсуждать, каким образом получены значения «весов» критериев. Будем считать, что ЛПР (лицо, принимающее решения) определили их и ввел в систему поддержки принятия решений в соответствии со своими предпочтениями. Таблица2.
Таблица 3.
Таблица 4.
Необходимо сопоставить предпочтения ЛПР на последнем уровне. Обозначим все пути, в частности, дуги lij через p(lij). Для таблиц типа 10.1.a p(lij) = для таблицы 1.a mA (AB1)=1, mA (AB2)=0.75, mA (AB3)=0.25. Система поддержки принятия решений находит p(АВ1)=0.5, p(АВ2)=0.36, p(АВ3)=0.13. Определение веса критерия, когда производится попарное сравнение весов (значимости) различных критериев, так ка это сделано в табл. 1.b, 5, 2. Сложность заключается в несогласованности оценок. Самым точным методом является нахождение главного собственного вектора матрицы, который после нормализации становится вектором приоритетов. Рассмотрим более простой метод. Представим количественные сравнения пар объектов матрицей А=(аij), (i,j =1,2,…..,n), где аij показывает оценку отношения между i-м и j-м объектами. Элементы матрицы обладают следующими свойствами: если аij=b, то аji=1/b, aii=1. Суммируем элементы каждой строки и нормализуем делением каждой суммы на сумму элементов. Сумма полученных результатов будет равна 1. Первый элемент результирующего вектора будет весом приоритета первого объекта, второй – второго и т.д. Так как это показано в таблице 6, при использовании табл. 1.b и значений лингвистических переменных табл.7.
Рис. 1 Таблица 5.
Таблица 6.
Таблица 7.
p(АВ1)=0.53, p(АВ2)=0.31, p(АВ3)=0.15.
Аналогично СППР находит веса приоритетов второго уровня. p(В1С1)=0.38, p(В1С2)=0.38, p(B1C3)=0.19; p(В1C4)=0.5, p(B2C5)=0.61, p(В2C6)=0.19, p(В2C7)=0.20, p(В3C8)=0.8, p(В3C9)=0.2.
Таблица 8.
Таблица 9.
Таблица 10.
Таблица 11.
Таблица 12.
Веса приоритетов второго уровня в графе являются уточнением влияния соответствующих факторов на принятие решения. Но они представляют интерес только с учетом весов первого уровня. Для нахождения весов путей, состоящих из дуг превого и второго уровней надо умножить вес дуги первого уровня на веса примыкающих к ней дуг второго уровня. Т.о. вес пути из дуг первого и второго уровней: p(l1i, lij) = p(l1i) ´ p(lij), где l1i – дуга первого уровня, lij – дуга второго уровня (i=1,….,n), (j=1,…..,m). Аналогично рассчитываются веса дуг следующих уровней. p(AB1C1)= p(AB1)´ p(B1C1) = 0.53´0.38=0.20 p(AB1C2)= p(AB1)´ p(B1C2) = 0.53´0.38=0.20 p(AB1C3)= p(AB1)´ p(B1C3) = 0.53´0.19=0.10 p(AB1C4)= p(AB1)´ p(B1C4) = 0.53´0.05=0.03 p(AB2C5)= p(AB2)´ p(B2C5) = 0.31´0.61=0.19 p(AB2C6)= p(AB2)´ p(B2C6) = 0.31´0.19=0.06 p(AB2C7)= p(AB2)´ p(B2C7) = 0.31´0.21=0.07 p(AB3C8)= p(AB3)´ p(B3C8) = 0.15´0.8=0.12 p(AB3C9)= p(AB3)´ p(B3C9) = 0.15´0.2=0.03
Оценка решений есть результат умножения матрицы весов дуг последнего уровня на вектор весов приоритетов вершин предпоследнего уровня графа.
где Если эксперту удалось свести задачу выбора лучшего решения к иерархической, то можно использовать описанный метод. 3.7 Задания для самостоятельного решения Вариант 1 Отдел кадров сузил поиск будущего сотрудника до трех кандидатур: Сергей (S), Женя (J) и Михаил (M). Конечный отбор основан на трех критериях: собеседование (С), опыт работы (О) и рекомендации (Р). Отдел кадров использует матрицу А (приведенную ниже для сравнения трех критериев. После проведен собеседования с тремя претендентами, сбор данных относящихся к опыту их работы и рекомендациям. Построены матрицы Ас, Ао и Ар. Кого из трех кандидатов следует принять на работу? Оценить согласованность данных.
Вариант 2 Костя и Динара Печкины (К и Д) покупают новый дом. Рассматриваются три варианта А, В, С. Печкины согласовали два критерия для выбора дома: площадь зеленой лужайки (Л) и близость к месту работы (Б), а также разработали матрицы сравнений, приведенные ниже. Необходимо оценить три дома в порядке их приоритета и вычислить коэффициент согласованности каждой матрицы.
Вариант 3 Найти веса распределения энергии для нескольких крупных потребителей в соответствии с их общим вкладом в различные цели общества. Есть три крупных потребителя США: Бытовое потребление (С1), Транспорт (С2) и промышленность (С3). Они составляют низший уровень иерархии. Целями, по отношению к которым оцениваются потребителя, являются: вклад в развитие экономики, вклад в качество окружающей среды и вклад в национальную безопасность. Они составляют торой уровень. Матрицы попарных сравнений приведены ниже.
Вариант 4 На первом уровне иерархии: Общий вклад в развитие На втором уровне – Железо (Ж), медь (М), фосфаты (Ф). На третьем уровне: Величина ресурса (ВР), Стоимость добычи (СД), Риск (Р).
Определить веса элементов третьего уровня.
Вариант 5 На первом уровне иерархии: Влияние в мире На втором уровне – Людские ресурсы (ЛР), Благосостояние (Б), Технология (Т), Военная мощь (ВМ). На третьем уровне: США, СССР, Китай.
Вариант 6
Аттестация преподавателей в высшей школе. Первый уровень – Аттестация. Второй уровень – Исследовательская работа (ИР), Преподавание (П). Третий уровень (Исследовательская работа) – Качество (К), Разнообразие (Р), Количество научных трудов (НТ), важность работы (ВР). Третий уровень (Преподавание) – Доходчивость (Д), Требовательность (Т), Правдивость (ПР).
Вариант 7 Переправа через реку Первый уровень – Выгоды переправы через реку. Второй уровень – Экономические (Э), Социальные (С), Окружающая среда (ОС). Третьий уровень – относятся к экономическим: Время (В), Доход (Д), Торговля (Т). К социальным: Безопасность (Б), Связи (СВ). К окружающей среде – комфорт (КО), Доступность (ДС). Четвертый уровень – Мост (М), Туннель (ТУ), существующий паром (П).
Вариант 8 Переправа через реку (2-я часть) Первый уровень - издержки пересечения реки. Второй уровень - Экономические (Э), Социальные (С), Окружающая среда (ОС). Третий уровень - относятся к экономическим: Капиталовложения (К), Эксплуатация и текущий ремонт (ЭТР), Прекращение паромного бизнеса (ППБ). К социальным: Изменение стиля жизни (ИСЖ), Раскол людей (РЛ). К окружающей среде – Загазованность (З), Загрязнение воды (ЗВ).
Вариант 9 Первый уровень - Качество жизни городского населения. Второй уровень – Уровень жизни (УР), Условия жизни (УС). Третий уровень – К уровню жизни относятся: Доходы населения (Дх), Социальное обеспечение (СО), Жилищные условия (Жу), Образование (Об), Здравоохранение (Зд); к Условиям жизни: Здравоохранение (Зд), Санитарные условия (Су), Условия для проведения досуга (Уд), Состояние транспорта (Тр), Экология (Эк), Психологическое состояние населения (Пх).
Вариант 10 На первом уровне – благосостояние страны. Второй уровень – Сильная экономика (Э), Благосостояние (Б), Национальная оборона (НО). Третий уровень – Тяжелая промышленность (ТП), Легкая промышленность (ЛП), Сельское хозяйство (СХ).
Определить веса отраслей промышленности по влиянии. На благосостояние этой страны. 4. Оптимальный объем заказа
Основной вопрос управления запасами заключается в определении товарного запаса на складе, чтобы минимизировать издержки по управлению запасами и обеспечить достойный уровень обслуживания клиента? Он разделяется на две части: Как сделать издержки управления запасами минимальными при заданном (постоянном или непостоянном, но известном) спросе? Как оценить риск возникновения дефицита на складе с учетом случайных вариаций реального спроса? Сколько нужно платить за содержание необходимого резервного запаса для того, чтобы снизить риск возникновения дефицита до приемлемого уровня и обеспечить достойный уровень обслуживания клиентов? Основная идея теории оптимального управления запасами состоит в том, чтобы разделить издержки на переменные и постоянные. Оказывается, что эти две группы издержек по-разному зависят от размера заказа и уровня запаса товара на складе. Переменные издержки- издержки хранения. Данные издержки должны быть прямо пропорциональны количеству единиц хранимых запасов и стоимости единицы запаса. Основную часть этих издержек составляют упущенные возможности при альтернативном использовании капитала, «замороженного» в запасах. Каждая область бизнеса характеризуется своей требуемой нормой доходности. Капитал, вложенный в этот бизнес, в среднем (по стране, региону, городу) должен давать определенный процент дохода ежегодно. Капитал, вложенный в запасы, такого процента не дает. Следовательно, неполученный процент – это издержка хранения. Если товар приобретен в кредит, то за этот кредит нужно платить проценты, что опять-таки составляет издержки хранения. При цивилизованном ведении бизнеса, товар должен быть застрахован и подлежит налогообложению. Страховка и налог на запас также составляет определенный процент от стоимости товара и также входит в издержки хранения. Перечисленные издержки строго пропорциональны стоимости запасов. Поэтому их удобно задавать в расчете на единицу запаса в год. Постоянные издержки - издержки по запуску новой партии продукции - (производство) или затраты на формирование и оформление заказа - (торговля). Эти издержки не зависят от величины предполагаемой партии продукции (заказа).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1702; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.255.247 (0.017 с.) |

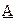 и
и 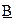 : [a1, a2] и [b1, b2], соответственно. Тогда основные операции с нечеткими числами сводятся к операциям с их интервалами достоверности. А операции с интервалами, в свою очередь, выражаются через операции с действительными числами - границами интервалов:
: [a1, a2] и [b1, b2], соответственно. Тогда основные операции с нечеткими числами сводятся к операциям с их интервалами достоверности. А операции с интервалами, в свою очередь, выражаются через операции с действительными числами - границами интервалов: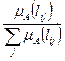
 (1)
(1)
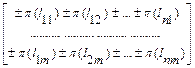
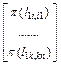 =
= 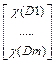 ,
,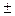 p(lij) – вес дуги, связывающей вершину i с вершиной последующего уровня j, p(l1r, lrj) –вес дуги, оканчивающейся в j-ой вершине предпоследнего уровня графа, фактически вес пути в графе, начинающийся с исходной вершины и кончающийся в j-ой вершине предпоследнего уровня. c(Dp) – вес p-ой конечной вершины (p-го варианта решения).
p(lij) – вес дуги, связывающей вершину i с вершиной последующего уровня j, p(l1r, lrj) –вес дуги, оканчивающейся в j-ой вершине предпоследнего уровня графа, фактически вес пути в графе, начинающийся с исходной вершины и кончающийся в j-ой вершине предпоследнего уровня. c(Dp) – вес p-ой конечной вершины (p-го варианта решения).


