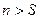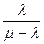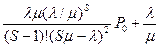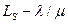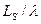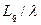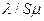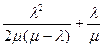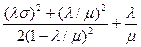Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация систем массового обслуживанияСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Системы массового обслуживания (СМО) классифицируются по трем основным признакам. 1. Популяция потенциальных клиентов (или «резервуар» из которого приходят заявки) и характеристики входного потока. 1.1 Популяция может быть бесконечной или конечной. - Бесконечной популяцию можно считать в том случае, если ее размер намного больше любого мыслимого размера очереди, который может возникнуть в данной СМО. При этом, интенсивность входного потока заявок не будет зависеть от того, сколько их уже поступило в систему. - Конечной мы будем называть такую популяцию, размер которой сравним с длиной очереди, образующейся в системе. Если, например, наладчик обслуживает 10 станков в цехе, и каждый станок останавливается и требует обслуживания в среднем 1 раз в час, то суммарный ожидаемый поток заявок будет 10 заявок в час. Если, однако, один станок (два или три станка) остановились, и наладчик занимается его обслуживанием, то ожидаемый суммарный поток новых заявок будет лишь 9 заявок в час (8 или 7), до тех пор пока остановившиеся станки опять на заработают. Именно поэтому для конечной популяции в качестве основной характеристики входного потока рассматривается не интенсивность потока заявок от всей популяции (как в случае бесконечной популяции), а интенсивность потока заявок от каждого члена популяции (которая остается постоянной независимо от размера очереди). 1.2 Входной поток может быть подразделен на два вида: - Пуассоновский - Не пуассоновский 2. Свойства самой очереди. 2.1 Размер очереди - Неограниченный. - Ограниченный. Ограничения на размер очереди могут быть обусловлены технологическими причинами. Например, автоматическая телефонная станция не может удержать в очереди больше 10 звонков. Если в то время, когда 10 клиентов ждут ответа оператора, позвонил 11-ый клиент, он услышит короткие гудки - «занято». Система отказала ему в обслуживании. Иногда можно использовать модель ограниченной очереди для описания психологических особенностей клиентов. Если исследования поведения ваших клиентов показывают, что они редко становятся в очередь, если в ней уже стоит, скажем, 5 человек, то приблизительно можно описать вашу СМО как систему с отказами, в которой не может находиться более 5 клиентов. 2.2 Дисциплина очереди - Первый пришел – первым обслужен (в российской терминологии – «живая очередь) - Наличие заявок с приоритетом (примеры из российской практики: зрители с биноклями образуют отдельную очередь в театральном гардеробе, ветераны и беременные женщины – без очереди и пр., данный случай не может быть описан в рамках этой теории) - Очередь с нетерпеливыми заявками (после некоторого критического времени ожидания определенная доля заявок уходит, не дождавшись обслуживания, данный случай не может быть описан в рамках этой теории). Мы будем рассматривать модели теории очередей только для простейшей дисциплины очереди «Первый пришел - первым обслужен». 3 Свойства каналов обслуживания 3.1 Число каналов - Один канал - Несколько каналов 3.2 Пропускная способность каналов - Одинаковая - Различная 3.3 Частотное распределение времени обслуживание - Экспоненциальное распределение - Произвольное распределение Мы будем рассматривать только модели с абсолютно одинаковыми каналами обслуживания, случайное время обслуживания в которых распределено экспоненциально. В большинстве случаев, плотность распределения времени обслуживания характеризуется кривой с максимумом так, что существует наиболее вероятное время обслуживания, а вероятности того, что на обслуживание будет затрачено очень маленькое или очень большое время, понижены. Однако, за исключением самого простого случая неограниченной очереди с одним каналом обслуживания, получить в конечной форме решения для моделей СМО с иным, кроме экспоненциального, распределением для времени обслуживания не удается. В тех случаях, когда невозможно использование конечных формул теории очередей, всегда есть возможность провести компьютерное моделирование системы массового обслуживания и, путем усреднения по многим реализациям случайного процесса, получить все необходимые характеристики ее работы. Теория очередей предполагает, что входной поток клиентов (или заявок на обслуживание) описывается вероятностной моделью, которая называется простейшим или пуассоновским потоком. Чтобы быть пуассоновским потоком, входной поток заявок должен обладать тремя свойствами. Он должен быть: ординарным, стационарным, без памяти. Ординарный - это значит, что все заявки поступают в систему по одной, а не группами. Например, если группа студентов в перерыв между парами устремляется в буфет, свойство ординарности потока нарушается, и правильно описать такую ситуацию теория очередей не сможет. Свойство стационарности означает неизменность потока во времени. Требование стационарности не означает, разумеется, что в каждый час, минуту или день в систему приходит одинаковое число заявок. Теория очередей рассматривает входной поток как случайный, т.е. если взять два последовательных и равных промежутка времени, то в систему будет приходить разное (случайное) число заявок. Однако среднее число заявок, взятое по большому числу реализаций случайного процесса, в каждом равном промежутке времени будет одно и то же. Если, например, наблюдая некоторую столовую изо дня в день, мы обнаружим, что входной поток клиентов (а с ним и очередь) нарастает с момента открытия в 10 часов утра и достигает максимума в «часы пик» от 13 до 14, а затем идет на убыль, то свойство стационарности не выполняется. Свойство отсутствие памяти означает, что вероятность поступления в систему очередной заявки в следующий час или минуту, совершенно не зависит от того, сколько времени прошло с момента поступления предыдущей заявки. Заявки поступают в систему независимо друг от друга, и очередная заявка «не знает» (и потому «не может помнить») когда пришла предыдущая. Если вы ждете троллейбус на остановке уже 15 минут (а на табличке написано, что средний промежуток времени между ними составляет 5 минут), то, вместе со все возрастающим чувством досады, растет и вероятность того, что он все-таки придет в следующую минуту. В движении троллейбусов есть следы расписания. Хотя из-за случайных вариаций во времени обработки на предыдущих производственных этапах, детали на конвейер могут поступать в случайные моменты времени, «память» (или «следы расписания») в этом потоке, несомненно, присутствует. Применение формул теории очередей к таким процессам (по крайней мере, без всяких поправочных коэффициентов) неправомерно. А вот для потоков клиентов или заявок в системы массового обслуживания отсутствие памяти это очень характерное свойство. Неважно, когда поступила предыдущая заявка, вероятность ∆ P того, что новая заявка поступит в следующий промежуток времени ∆ t, будет равна
где Пусть P(t) – это вероятность того, что за время t в систему не поступит ни одной заявки, а P(t+ ∆ t) – вероятность того, что и за время t+ ∆ t ни одной заявки в систему не придет. Тогда очевидно, что между двумя вероятностями существует следующая связь:
т.е. вероятность того, что заявка не поступит в систему за время t+ ∆ t есть произведение вероятностей двух независимых событий: 1) заявка не поступила в сиcтему за время t и 2) заявка не поступила в систему за следующий малый промежуток времени ∆ t. Если раскрыть скобки, можно получить следующее дифференциальное уравнение:
Для читателей, знакомых с элементами дифференциального и интегрального исчисления, из (3) нетрудно получить, что выражение для вероятности того, что за время t в систему не поступит ни одной заявки:
а вероятность того, что за время t в систему поступит хотя бы одна заявка, будет, очевидно, выражаться формулой:
Из формулы (5) следует, что частотное распределение для промежутка времени между последовательными заявками, поступившими в систему, будет экспоненциальным распределением.
5.2. Расчеты характеристик СМО с помощью теории очередей . Введем стандартные обозначения: S – число серверов (каналов обслуживания)
заявок)
K – максимальное количество клиентов, которые могут находится в системе (или число членов конечной популяции)
Будем рассматривать модели очередей. Модель M/M/S – это модель неограниченной очереди, заявки в которую поступают из бесконечной популяции, поток заявок - пуассоновский, распределение времени обслуживания - экспоненциальное, в системе S серверов (каналов обслуживания). Первая буква М обозначает Марковский процесс для входного потока заявок (синоним пуассоновского потока). Вторая буква М обозначает, что и поток обслуженных заявок описывается Марковским процессом (время обслуживания распределено экспоненциально). Буква S обозначает, что в системе S каналов обслуживания. Модель M/M/1 – частный случай модели M/M/S, где число серверов S=1 Ниже, в таблице приведены формулы для расчета основных характеристик СМО.
Для простейшей модели неограниченной очереди с одним сервером, известны конечные формулы для средних характеристик очереди и в случае произвольного распределения вероятностей для времени обслуживания. Эти модели обозначаются как М/D/1 – для случая пуассоновского входного потока, но постоянного времени обслуживания и М/G/1 для произвольного распределения вероятностей времени обслуживания.
Пример решения задачи Банк планирует открыть банкомат для получения денег, не выходя из машины. Оценки показывают, что поток клиентов в рабочие дни - 15 машин/ в час. Банкомат тратит на обслуживание клиента в среднем 3 минуты. Предполагая пуассоновский поток заявок и экспоненциальное распределение для времени обслуживания найти: a. Долю времени, когда банкомат загружен; b. Долю времени, когда он бездействует; c. Среднее число машин у банкомата; d. Среднее число машин в очереди у банкомата; e. Среднее время, затрачиваемое клиентом для получения денег; f. Среднее время, которое клиент проводит в очереди; g. С какой вероятностью возле банкомата будут стоять более 3 машин. 2. Предположите, что время обслуживания клиента распределено нормально со средним значением 3 мин и стандартным отклонением: h. 3 мин, i. 1 мин, j. 0 мин, (постоянное время обслуживания). Определите, как изменятся характеристики системы. 3. Поскольку банкомат будет расположен на оживленной улице, не более трех машин могут стоять возле него. Если три машины стоят у банкомата, остальным негде остановиться, и они проезжают мимо. k. Какое количество клиентов будет терять банк в таком случае? l. Каковы характеристики СМО в этом случае? 4. Пусть банк решил поставить два банкомата рядом так, что машина может подъехать к любому свободному. При этом m. Жесткое ограничение на длину очереди снято, но крайне желательно, чтобы у банкоматов было не больше 3 машин. Какова вероятность, что в очереди действительно будет не более 3 машин. Как изменятся характеристики СМО? n. Жесткое ограничение на количество машин у банкомата сохранено. Какое количество клиентов будет терять банк в таком случае? Каковы характеристики СМО в этом случае?
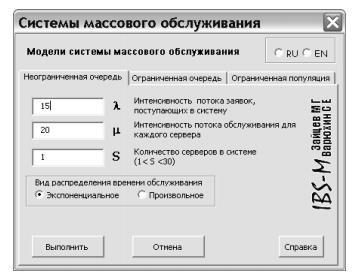
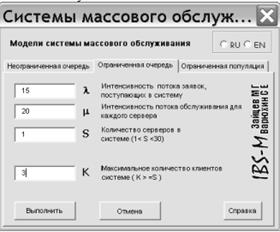
Решение задачи. Формулы для расчетов характеристик систем массового обслуживания в основном довольно громоздкие и, что хуже всего, их часто даже в Excel невозможно использовать, введя один раз, для расчета систем массового обслуживания просто меняя параметры λ, μ и проч. Сначала определим модель системы массового обслуживания, применимую для данного случая. Наиболее важные обстоятельства в этом случае – наличие небольшой популяции клиентов или ограничения на размер очереди. Так как никаких упоминаний о подобных ограничениях в задаче нет, считаем, что имеем дело с моделью неограниченной очереди. Кроме того, речь идет только об одном банкомате, т.о. в системе имеется только один сервер. Поток клиентов λ, прибывающих на вход в систему, равен 15 машинам в час. Кроме этого известно, что на обслуживание клиента в среднем тратится 3 минуты. Это означает, что за час в среднем обслуживается 20 клиентов, т.е. поток обслуживания μ равен 20 машин в час. По формулам для модели М/М/1 можно убедиться, что все необходимые для расчета данные у нас есть. Решать данную задачу мы будем с помощью надстройки для Excel, (разработанную Зайцевым М.Г. и Варюхиным С.Е.). Вызываем надстройку «Расчет параметров СМО», появляется следующее диалоговое окно (Рис. 1).
Рис.1
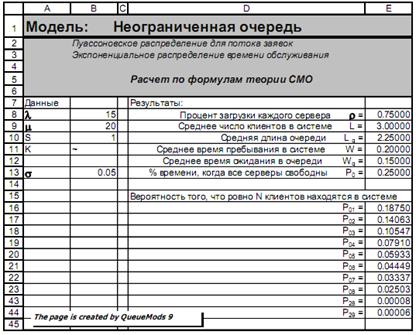
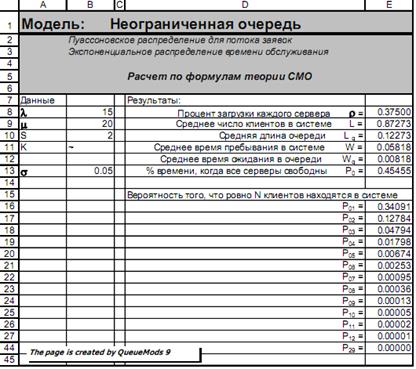
В диалоговом окне надстройки имеется три вкладки: неограниченная очередь, ограниченная очередь и ограниченная популяция. Так как решили, что данная задача решается в модели неограниченной очереди, останемся на вкладке, открытой по умолчанию. Щелкнем левой кнопкой мыши в окне λ – интенсивность потока заявок, и введем значение 15. Далее, переходя к остальным двум окнам ввода, задаем значение интенсивности потока обслуживания μ = 20 и количество серверов S = 1. В задаче оговорено, что время обслуживания распределено экспоненциально, поэтому мы оставим без изменения включенную по умолчанию кнопку Вид распределения - Экспоненциальное. Нажимаем кнопку «Выполнить» и в активную книгу Excel (книгу, с которой вы работаете в момент вызова надстройки), добавится новый лист с результатами расчета. На рисунке (Рис. 2) показан вид нового листа.
Рис. 2
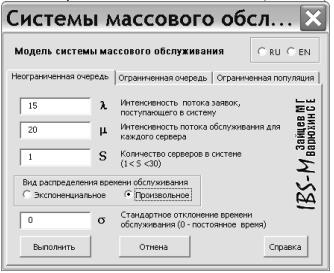
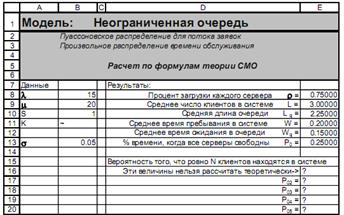
В заголовке указана использованная модель – неограниченная очередь, один сервер, экспоненциальное распределение времени обслуживания. С левой стороны приведены значения параметров очереди, которые мы задали: λ, μ и S. Кроме этого, приведено и вычисленное значение стандартного отклонения для экспоненциального распределения времени обслуживания, которое равно 1/μ. В правом столбце результат расчета, из которого можем почерпнуть информацию для ответов на вопросы первой части задачи. Доля времени, когда банкомат загружен равна проценту загрузки каждого (в нашем случае единственного) сервера, т.е 75% всего времени работы. Разумеется, это средняя оценка, которую можно было бы сделать по многим наблюдениям за системой. Доля времени, когда банкомат бездействует, равна времени, когда все серверы свободны – 25% рабочего времени. Среднее число машин у банкомата соответствует числу клиентов в системе – 3 клиента. В это число входит и та машина, которая стоит у банкомата и те, которые ждут своей очереди на подъездной дорожке. Средняя длина очереди – 2.25 клиента – показывает среднее число машин в очереди у банкомата. В среднее время, затрачиваемое клиентом для получения денег, входит и время, затраченное на ожидание в очереди, и время, которое клиент тратит на ввод информации в банкомат и ожидание транзакции (3 минуты в среднем), т.е. это полное время пребывания в системе. Это время приводится в таблице в тех же единицах, для которых задан поток – в часах. Следовательно, это время равно 0.2 часа или 12 минут. Среднее время, которое клиент проводит в очереди равно 0.15 часа или 9 минут. В нижней части таблицы приведены вероятности нахождения в системе заданного числа клиентов (от 1 до 29, но часть строк скрыта для экономии места). Вероятность того, что у банкомата будет стоять не более 3 машин, т.е либо ни одной (% времени, когда все серверы свободны), либо одна, либо две, либо три машины можно легко найти, сложив соответствующие вероятности: Pn<=3 = 0.25000 +0.18750 +0.14063 +0.10547 = 0.68359 (~ 68%). После этого можно определить и вероятность того, что в очереди будет более трех машин Pn>3, как 1 - Pn<=3. Pn>3= 0.31641 (~32%). Очевидно, что другой возможный путь – суммирование всех вероятностей для n>3 – гораздо менее удобен, но тоже применим, особенно если эти вероятности быстро падают до нуля. В данной задаче это не так, потому что даже вероятность того, что в системе n=29 клиентов отлична от нуля. Во второй части задачи нам предлагается оценить параметры модели и ответить на те же вопросы, в условиях, когда время обслуживания распределено нормально с заданным стандартным отклонением. Мы можем сделать это, изменив параметры модели. Вызовем надстройку «Расчет параметров СМО» еще раз. Если вы не закрывали книгу Excel, после того, как провели предыдущий расчет, то при вызове надстройки в ней сохранятся последние введенные данные. Но теперь мы кликнем мышкой отключенную по умолчанию кнопку Вид распределения - Произвольное. При этом вид окна изменится (Рис. 3)
Рис. 3
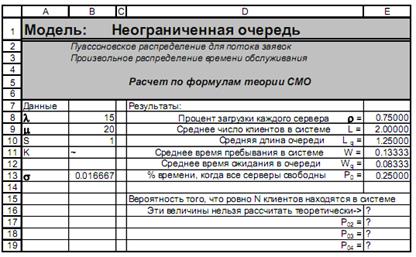
В появившемся окне σ можно задать стандартное отклонение времени обслуживания. Нужно только снова перевести его в те же единицы времени, для которых рассчитаны потоки – в часы. Итак: При стандартном отклонении 3 минуты и среднем значении времени обслуживания те же 3 минуты мы получаем, что и среднее время обслуживания и стандартное отклонение равны 0.05 часа. Записываем это значение в окне σ и вновь нажимаем кнопку Выполнить. В новом листе будут записаны следующие данные (Рис. 4).
Рис.4
Как мы видим, все числа в столбце E8:E13 в точности совпадают с результатами предыдущего расчета характеристик системы массового обслуживания (Рис. 2). Обратите внимание на значение σ в предыдущем расчете – оно также равно 0.05. Понятно, что сделанный только что расчет для распределения произвольного вида обязан не противоречить расчету, в котором вид распределения задан явно, если стандартное отклонение в обоих случаях совпадает. В последнем расчете отсутствуют значения вероятности наличия в очереди 1-го, 2-х, 3-х и т.д. клиентов, т.к. эти величины можно рассчитать только для экспоненциального распределения времени обслуживания. Если бы мы смоделировали СМО с характеристиками, заданными в пункте h, то обнаружили бы, что разный вид распределения времени обслуживания приводит к различным значениям вероятностей P1, P2, P3 и так далее. Но по формулам это рассчитать невозможно (кроме случая с экспоненциальным распределением). Поэтому надстройка выдает характеристики, зависящие от стандартного отклонения σ, но не зависящие от вида распределения. Остается убедиться в том, что надстройка выдает и результаты, которые невозможно получить при экспоненциальном распределении времени обслуживания. Для этого зададим стандартное отклонение σ, равное 1 мин. Так как 1 мин составляет 1/60 часть часа, то теперь в окне σ нужно задать 1/60 ≈0.016667 и вновь нажать кнопку «Выполнить» Результат показан на следующем рисунке (Рис. 5).
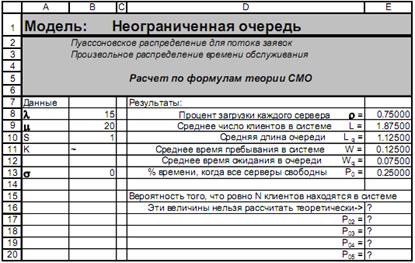
Рис. 5 В целом, полученные данные свидетельствуют о том, что характеристики СМО улучшились. Уменьшилась длина очереди с 2.25 клиента до 1.25 клиента и уменьшились время пребывания в системе и в очереди. Значение коэффициента утилизации (процент загрузки сервера) при этом не изменяется, так как оно не зависит от σ. Теперь зададим стандартное отклонение, равное 0 минут. При этом σ = 0, т.е. время обслуживания постоянно и в точности равно 3 мин. Можно ожидать, что в этом случае характеристики очереди еще улучшатся. И в самом деле, как мы видим на рисунке (Рис. 6), время пребывания в очереди снова уменьшилось.
Рис. 6
В третьей части задания речь идет о новом типе системы массового обслуживания – системе с ограниченной очередью. До этого момента мы использовали для расчетов вкладку Неограниченная очередь, Теперь, щелкнув по ярлыку вкладки Ограниченная очередь перейдем к новой панели надстройки (Рис.7). Здесь к трем параметрам, аналогичным параметрам модели неограниченной очереди, добавляется еще один – максимальное количество клиентов в системе. (Иногда этот параметр называют максимальная длина очереди, но в этом случае он равен K-S, т.е. максимальное количество клиентов в системе минус число серверов. Это отличие следует учитывать при пользовании другими способами расчета характеристик СМО.) По условию задачи у банкомата не может стоять более 3-х машин, т.е. максимальное количество клиентов в системе – 3. Априори ясно, что при одном банкомате-сервере максимальная длина очереди не может превышать 2 машины.
Рис. 7
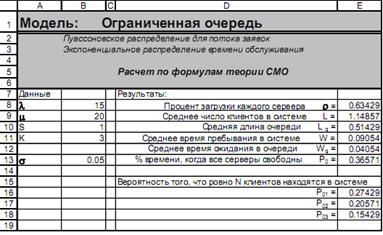
На следующем рисунке (Рис. 8) показаны результаты расчета. Вверху листа кратко охарактеризована использованная модель – ограниченная очередь, один сервер. Сравнение характеристик СМО из столбца E8:E13 с результатами, полученными ранее, показывают, что качество системы вроде бы снова улучшилось, даже по сравнению со случаем постоянного времени обслуживания. Однако это улучшение не является безусловным.
Рис. 8
Не зря в этом вопросе задачи говорится о количестве потерянных клиентов. Ведь как только из-за случайных колебаний потока клиентов и потока обслуживания очередь у банкомата достигнет двух машин (+ одна под обслуживанием), все новые потенциальные клиенты вынуждены будут проезжать мимо до тех пор, пока очередь не уменьшится до одной машины. Следовательно, улучшение характеристик СМО произошло фактически за счет потери части клиентов. В данном случае потерянные клиенты – потерянные деньги и у владельца банкомата есть все основания не слишком радоваться характеристикам своей СМО. Впрочем, в данном случае у нас нет информации об экономических характеристиках ситуации – например, прибыли с одного клиента, арендной плате за установку банкомата и изменении этой платы в случае удлинения подъездной дорожки и проч. - так что делать обоснованные экономические выводы мы не можем. Однако можно оценить среднее число потерянных клиентов. Для этого нужно сформулировать, в каких условиях теряется клиент. Мы уже отметили, что клиент теряется тогда, когда очередь у банкомата максимальна и равна 2 машинам. В этом случае общее количество клиентов в системе равно 3. Посмотрим, чему же равна вероятность такого события. Из результатов расчета (Рис. 8) следует, что P3=0.15429. Т.е. теряется чуть более 15% всех потенциальных клиентов. А общее количество потенциальных клиентов (поток клиентов λ) равно 15 в час. Таким образом, из этих 15 клиентов в среднем 2.31429 клиента будет потеряно, а прибыль получена только от 12.6857 клиентов в час. То обстоятельство, что часть клиентов теряется, не только приводит к тому, что среднее число клиентов в системе, средняя длина очереди, среднее время пребывания в системе и среднее время пребывания в очереди уменьшаются в сравнении с СМО с неограниченной очередью. Уменьшается и процент загрузки сервера (0.63429 вместо 0.75) и, следовательно, его экономическая эффективность. В четвертой части задачи используются обе рассмотренные модели СМО, изменяется только количество серверов-банкоматов. Вызовем еще раз надстройку Расчет параметров СМО, вернемся на первую вкладку Неограниченная очередь и изменим количество серверов до 2. Если по ходу решения задачи вы не закрывали Excel, то на вкладке должны были сохраниться последние установки – произвольное распределение времени обслуживания со стандартным отклонением 0. Как только вы измените количество серверов на 2, вид распределения времени обслуживания автоматически изменится на экспоненциальное и окно выбора значения стандартного отклонения закроется. Это связано с тем, что формулы для расчета характеристик СМО при произвольном распределении времени обслуживания существуют только для случая, когда в системе один сервер. Если серверов больше, установить характеристики СМО можно только прямым моделированием. Результат расчета приведен на Рис. 9. Очевидно, что характеристики системы улучшились. Среднее время пребывания в очереди стало меньше полуминуты (0.008 часа). Оценим теперь вероятность того, что в системе будет более 3 клиентов. Сумма вероятностей отсутствия клиентов в системе (0.45454), одного клиента в системе (0.34091), двух и трех клиентов в системе (0.12784 и 0.04794) равна 0.97124. Следовательно, только 2,88% случаев количество машин у банкоматов будет превышать 3. Это, судя по всему, вполне удовлетворяет критерию «крайне нежелательно». При этом все же вполне вероятно, что в системе будет 5, 6, 7 и более клиентов. Нетрудно подсчитать, что примерно в течение 1 минуты за две недели в системе может быть даже 10 клиентов.
Рис. 9
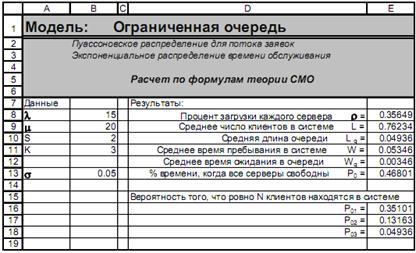
Для ответа на последний вопрос задачи вернемся еще раз на вкладку Ограниченная очередь и изменим количество серверов. Как показывает Рис. 10, в сравнении с предыдущим расчетом (пункт m) процент загрузки серверов немного упал (0.35649 против 0.375).
Рис. 10
Это вызвано, очевидно, потерей некоторой части клиентов. Сравнивая числа в ячейках E18 на Рис. 8 и Рис. 10, мы можем видеть, что при переходе от одного банкомата к двум доля потерянных клиентов снижается более чем в 3 раза и становится чуть меньшей 5%. Но все же часть клиентов все равно теряется (примерно 0.74 клиента в час) и процент загрузки серверов падает.
5.3. Задачи для самостоятельного решения.
Вариант 1. Автоматическая телефонная система заказа билетов может поставить в очередь максимум 3-х клиентов. Оператор тратит в среднем на принятие заказа по телефону 4 мин. Звонки поступают в среднем 1 раз в 5 мин. Распределение времени обслуживания и интервала времени между звонками – экспоненциальное. a. Определите среднее число звонков, ждущих ответа оператора. b. Каково среднее время ожидания ответа? c. Какова вероятность того, что позвонивший клиент должен будет ждать. d. Найдите процент звонков, которым будет отказано в постановке в очередь на ожидание ответа
Вариант 2. На пропускной таможенный пункт на границе прибывает в среднем 6 грузовых машин в час (пуассоновский поток). Работает три бригады квалифицированных таможенников, каждая из которых может осмотреть машину в среднем за 20 мин (распределение экспоненциальное). a. Какова средняя длина очереди? b. Сколько в среднем каждая машина тратит на проезд через таможенный пункт? c. Сколько времени таможенная бригада не занята? d. Руководство Таможенной службы ввело новые правила регистрации грузов, вследствие чего среднее время досмотра увеличилось до 38 мин. Как изменится время проезда через пропускной пункт, если невозможно увеличить кадровый состав таможенного пункта больше чем на 1 бригаду. e. Какова вероятность того, что в очереди в этом случае будут стоять не менее 10-и машин? … 20-и машин?
Вариант 3. В цехе находится большое количество автоматических станков. В среднем 1 раз в 2 часа один из станков останавливается и требует замены деталей, (случайные моменты остановки распределены в соответствие с распределением Пуассона). Когда происходит остановка станка, техник диагностирует причины остановки и производит замену необходимой детали. Среднее время нахождения неисправности и нахождения и установки нужной детали– 30 мин. (это время распределено экспоненциально). Оплата техника составляет $30 в час. Простой оборудования - $400 в час. Определите: a. Среднее число машин, находящихся в ремонте? b. Среднее время простоя остановившейся машины? c. Каково должно быть оптимальное число техников в цехе?
Вариант 4. Клиенты входят в приемную в среднем по шесть в час. Отделение укомплектовано одним служащим, который тратит на работу с клиентом около шести минут. Предположите, что прибытие клиентов соответствует Пуассоновскому потоку, а время обслуживания имеет экспоненциальное распределение. a. Как случайный наблюдатель, сколько людей Вы ожидали бы видеть в приемной (исключая самого клерка)? Как долго клиент будет находиться в приемной? b. Каков коэффициент использования рабочего времени клерка? c. Какова вероятность того, что более двух клиентов будут находиться в приемной? d. Другой такой же клерк нанят для той же работы. Как долго клиент будет проводить в приемной теперь?
Вариант 5. Ресторан «Ешь вволю» (плати 500 рублей и ешь, что хочешь хоть целый день) имеет две кассы для продажи входных билетов с двух разных сторон заведения. Наблюдения показывают, что в воскресный день к каждому из входов прибывает посетитель примерно один раз в шесть минут. Входное обслуживание каждого клиента занимает в среднем 4 минуты. a. Сколько процентов времени каждая из касс свободна? Какова вероятность, что обе кассы свободны? b. Сколько в среднем посетителей ждут обслуживания в каждой очереди? Сколько в среднем времени каждый посетитель вынужден ожидать в очереди? c. Ресторан рассматривает вариант объединения двух касс при одном единственном входе в ресторан. Кассы будут работать с той же скоростью. Каковы будут характеристики такой системы обслуживания? Стоит ли провести такую реорганизацию?
Вариант 6 Магазин успешно торгует по каталогам, и клерк принимает заказы по телефону. Если он занимает линию, автоответчик предлагает клиенту подождать. Как только клерк освобождается, заказы, которые ждали дольше, обслуживаются первыми. Заказы приходят со скоростью 12 в час. Клерк способен обслужить один заказ в среднем за 4 мин. Звонки поступают по закону Пуассона, а время обслуживания подчинено экспоненциальному закону. Клерк получает 150 рублей в час, но потери продаж оцениваются в 750 рублей за час ожидания в очереди. a. Какое среднее время должен ждать клиент в очереди, прежде чем ему ответит клерк? b. Каково среднее число заказчиков в очереди? c. Менеджер решил добавить второго клерка на оформление заказов, его зарплата тоже 150 рублей в час. Нужен ли второй клерк? d. А третий? Обоснуйте свой ответ.
Вариант 7 На пропускной таможенный пункт на границе прибывает в среднем 5 грузовых машин в час (пуассоновский поток). Работает две бригады квалифицированных таможенников, которые могут осмотреть машину в среднем за 20 мин (распределение экспоненциальное). a. Какова средняя длина очереди? b. Сколько в среднем каждая машина тратит на проезд через таможенный пункт? c. Сколько времени каждая таможенная бригада не занята? d. Руководство Таможенной службы ввело новые правила регистрации грузов, вследствие чего среднее время досмотра увеличилось до 45 мин. Как изменится время проезда через пропускной пункт, если невозможно увеличить кадровый состав таможенного пункта больше чем на 2 бригады. e. Какова вероятность того, что в очереди в этом случае будут стоять не менее 11-и машин? … 19-и машин?
Вариант 8. Бармен может обслужить клиента в среднем за 40 сек. (распределение экспоненциальное). В вечернее время бар практически заполнен и в среднем каждую минуту клиент подходит к стойке. (Бар очень большой). a. Как долго (в среднем) клиент будет ждать у стойки? b. Сколько в среднем людей будет толпиться у стойки? c. Какова вероятность, что 5 и более посетителей будут ждать выпивки? d. Каков процент времени, когда бармен не занят? e. Если заменить бармена разливочным автоматом, который на любой коктейль тратит одно и то же время – 45 сек., как изменятся рассчитанные выше характеристик
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1975; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.253.224 (0.019 с.) |

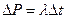
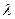 - это интенсивность входного потока заявок, т.е. среднее число заявок, поступающих в единицу времени. Это равенство будет выполняться тем точнее, чем меньше выбранный промежуток времени, при условии, что
- это интенсивность входного потока заявок, т.е. среднее число заявок, поступающих в единицу времени. Это равенство будет выполняться тем точнее, чем меньше выбранный промежуток времени, при условии, что 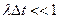 .
.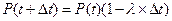 , (2)
, (2)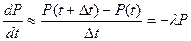 (3)
(3)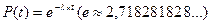 , (4)
, (4)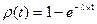 (5)
(5)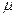 – средняя скорость обслуживания для каждого сервера.
– средняя скорость обслуживания для каждого сервера.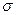 – стандартное отклонение времени обслуживания
– стандартное отклонение времени обслуживания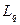 – средняя длина очереди (число ждущих, но не обслуживаемых клиентов)
– средняя длина очереди (число ждущих, но не обслуживаемых клиентов)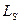 – среднее число клиентов в системе
– среднее число клиентов в системе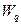 – среднее время ожидания в очереди
– среднее время ожидания в очереди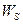 – среднее время пребывания клиента в системе (ожидание плюс обслуживание)
– среднее время пребывания клиента в системе (ожидание плюс обслуживание)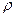 – коэффициент утилизации (процент загрузки) любого из серверов системы
– коэффициент утилизации (процент загрузки) любого из серверов системы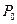 – вероятность отсутствия клиентов в системе
– вероятность отсутствия клиентов в системе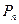 – вероятность того, что в системе ровно n клиентов
– вероятность того, что в системе ровно n клиентов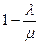

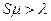



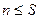 или
или