
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Наименование темы: Классификация систем массового обслуживания. Формула ЛиттлаСодержание книги
Поиск на нашем сайте
Классификация систем массового обслуживания. Используется трех -, четырех -, шести – компонентное символическое обозначение системы массового обслуживания, предложенное Кендаллом (Candall) и развитое в работах Г.П.Барашина. A/b/c:d/e/f a – распределение поступающего потока запросов. b – закон распределения времени обслуживания. Типовые условные обозначения: М – экспоненциальное (Марковское) распределение, D – детерминированное распределение, Ek – эрланговское распределение k-го порядка, HMk – гиперэкспоненциальное, HEk – гиперэрланговское распределение порядка k, GI – произвольное распределение независимых промежутков между заявками, G – произвольное распределение длительностей обслуживания. c – структура системы обслуживания (обычно число серверов). d – дисциплина обслуживания (параметры после двоеточия иногда опускают). Обычно используется сокращенное символическое обозначение, например FF вместо FIFO, LF, PR и т.п. e – максимальное число запросов, воспринимаемое системой, может употребляться символ ¥. f – максимальное число запросов к системе обслуживания. В некоторых публикациях последними символами отражают качественные характеристики системы обслуживания. Некоторые общие результаты и основы математического аппарата, необходимого для анализа можно получить, рассматривая системы G/G/m. Формула Литтла (Little). Рассмотрим временную диаграмму работы системы массового обслуживания (рис. 1), отразив на ней последовательность поступления требований, помещение требований в очередь и обработки серверами системы.
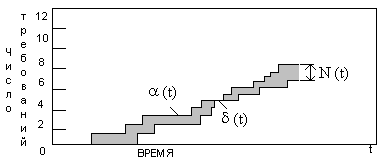
С увеличением числа требований растет время ожидания. Установим соотношение между средним числом требований в системе, интенсивностью потока и среднего времени пребывания в системе. Обозначим число поступающих в промежутке времени (0, t) требований как функцию времени α(t). Число исходящих из системы заявок (обслуженных) на этом интервале обозначим δ(t). На рисунке 2 показаны примеры функциональных зависимостей этих двух случайных процессов от времени.
Рис. 2 Зависимость между средним числом требований в системе, интенсивностью потока и средним времени пребывания в системе.
Число требований, находящихся в системе в момент t будет равно:
Площадь между двумя рассматриваемыми кривыми от 0 до t - дает общее время, проведенное всеми заявками в системе за время t. Обозначим эту накопленную величину γ(t). Если интенсивность входного потока равна λ, а средняя интенсивность за время t:
Наконец, определим среднее число требований в системе в промежутке (0,t):
Из последних трех уравнений следует, что: Если в СМО существует стационарный режим, то при t → ∞, будут иметь место соотношения:
Последнее соотношение означает, что среднее число заявок в системе равно произведению интенсивности поступления требований в систему на среднее время пребывания в системе. При этом не накладывается никаких ограничений на распределения входного потока и времени обслуживания. Впервые доказательство этого факта дал Дж.Литтл и это соотношение носит название формула Литтла. Интересно, что в качестве СМО можно рассмотреть только очередь из заявок в буфере. Тогда формула Литтла приобретает иной смысл - средняя длина очереди равна произведению интенсивности входного потока заявок на среднее время ожидания в очереди: Если наоборот рассматривать СМО только как серверы, то формула Литтла дает:
где В любом случае: Одним из основных параметров, которые используются при описании СМО, является коэффициент использования (utilization factor). Это фундаментальный параметр, так как он определяется как отношение интенсивности входного потока к пропускной способности системы. Поскольку пропускная способность СМО содержащей m серверов может быть определена как:
Нетрудно видеть, что коэффициент использования равен в точности интенсивности нагрузки, если СМО с одним сервером и в m раз меньше для систем с m серверами. Величина коэффициента использования равна среднему значению от доли занятых серверов и Если в СМО типа G/G/1 существует стационарный режим и можно определить вероятность того, что в некоторый случайный момент сервер будет свободный, то
СРС 3 по дисциплине “Теория распределение информации» Наименование темы: Стационарные вероятности рк для СМО типа М/М/1. На рис. 1 приведен график вероятностей того, что в очереди находится k заявок в установившемся режиме.
Рис. 1 Стационарные вероятности рк для СМО типа М/М/1. Важной характеристикой системы является средняя длина очереди. Зная вероятности каждого из возможных значений длины, найдем математическое ожидание:
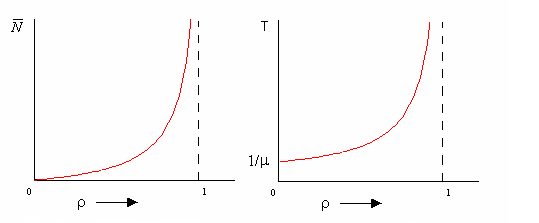
График средней длины очереди заявок в системе в зависимости от значения коэффициента использования или нагрузки показан на рис. 2. Найдем теперь дисперсию длины очереди:
Рисунок 2 Среднее число требований Рисунок 3 Среднее время пребывания в системе типа М/М/1 требования в системе типа М/М/1 как функция ⍴
Для нахождения среднего значения времени пребывания в очереди воспользуемся формулой Литтла.
На рис. 3 приведен график зависимости среднего времени пребывания в очереди в зависимости от коэффициента использования (нагрузки). При увеличении коэффициента использования, длина очереди, так и время пребывания в ней неограниченно возрастают при приближении ρ к единице. Такой вид зависимости от коэффициента использования характерен для почти всех СМО. Наконец найдем вероятность того, что в очереди будет находиться не менее чем k заявок и того, что в очереди менее k заявок.
Итак, в ходе анализа простейшей системы М/М/1 удалось в аналитическом виде найти все практически интересные характеристики QoS системы.
СРС 4 по дисциплине “Теория распределение информации»
|
||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 779; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.116.77 (0.008 с.) |

 .
. ,то время, проведенное одной заявкой в системе, усредненное по всем заявкам будет равно:
,то время, проведенное одной заявкой в системе, усредненное по всем заявкам будет равно: .
. .
. , (где
, (где  ).
).

 .
. ,
, – среднее число заявок в серверах, а
– среднее число заявок в серверах, а  – среднее время обработки в сервере.
– среднее время обработки в сервере.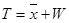 .
.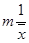 , то коэффициент использования может быть определен как:
, то коэффициент использования может быть определен как: .
. .
. .
.
 .
. .
.
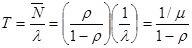 .
.




