
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Система с несколькими серверами: M/M/mСодержание книги
Поиск на нашем сайте Система обслуживания с m серверами явными потерями: M/M/m/Loss Система с несколькими серверами: M/M/m Рассмотрим сначала простой случай системы, содержащей два сервера, любой из которых доступен для поступающих на вход заявок. Системы с несколькими серверами такого типа называют полнодоступными. По сравнению с односерверной системой производительность будет выше. Сравнение с односерверной системой интенсивность обслуживания в которой в среднем вдвое выше, то есть мы ответим на вопрос что эффективнее удвоение скорости обработки или распараллеливание обработки.
Система M/M/2 может быть представлена как процесс размножения-гибели с параметрами:
Таким образом, в системе с двумя серверами время задержки сокращается. Нетрудно убедиться, что производительность системы M/M/2 также выше. Получилось, что производительность системы без блокировки также как и для системы с одним сервером совпадает с входной нагрузкой, тогда как максимальная производительность могла равняться 2μ. Найдем теперь для сравнения характеристики качества обслуживания для односерверной системы с вдвое большей пропускной способностью сервера μ.
Рис. 1. Нормированные графики среднего времени задержки в системе с одним и с двумя серверами одной и той же производительности и с одним серверов, работающим с вдвое большей скоростью. На рис 1. Представлены нормированные графики средгнего времени задержки в системе с одним и с двумя серверами одной и той же производительности и с одним серверов, работающим с вдвое большей скоростью. Как видно из сравнения, увелечение вдвое скорости работы сервера оказывается более эффективным, чем введение паралельного сервера той же производительности.
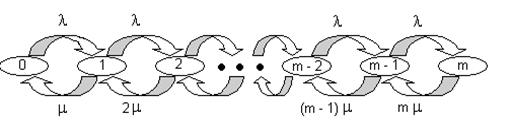
переходов для такой системы представлена на рис. 2. Рисунок 2. Диаграмма интенсивностей переходов для СМО типа M/M/m.
Интенсивности переходов могут быть определены следующим образом:
Система обслуживания с m серверами явными потерями: M/M/m/Loss Система без образования очереди для заявок, поступивших в моменты, когда все m серверов были заняты. Такие заявки будут просто теряться. В телефонии это типичный случай коммутирования на конечном коммутационном поле. Опишем такую систему подходящим процессом типа гибели-размножения. Его параметры могут быть определены так
Такая система оказывается также эргодичной и диаграмма интенсивностей переходов, приведенная на рис. 3
Рис. 3 Диаграмма интенсивностей переходов для СМО типа M/M/m:Loss. Основной характеристикой QoS для этой системы является средняя доля времени, когда все серверы оказываются занятыми. В этом случае говорят о том, что в системе наступила блокировка.
Лекция №5 по дисциплине “Теория распределение информации» Наименование темы: Анализ систем массового обслуживания с марковскими потоками требований Система типа M/M/m:m Вероятность занятия серверов
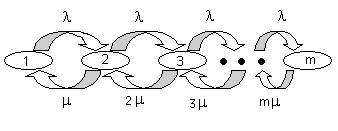
Система типа M/M/m:m Систему, имеющую одинаковое число входных линий и обслуживающих серверов, например выходных линий. Очевидно, что блокировка в такой системе невозможна. Диаграмма интенсивностей переходов состояний может быть представлена в виде совокупности несвязных m простейших подсистем с двумя состояниями – свободно/занято. (Рис. 1.20)
Рис. 1.20 Диаграмма интенсивностей переходов состояний для СМО типа M/M/m:m. Вероятности того, что k подсистем находятся в состоянии «занято», описывается формулой Энгсета:
Нетрудно видеть, что в этом случае в знаменателе записан бином Ньютона, и формула для вероятностей может быть существенно упрощена:
Полученное распределение вероятностей носит название биноминального или распределения Бернулли. Величина a определяет вероятность занятости сервера, а величина (1-a) – вероятность его простоя. Поскольку таких серверов m, то распределение вероятностей будет таким же, как для классической задачи о бросании m монет. Следует отметить также что
|
||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 898; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |







 .
.




