
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принятие решений при неизвестной априорнойСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Информации При рассмотрении критериев для принятия решений в условиях риска предполагается, что распределения вероятностей либо известны, либо могут быть найдены. Эти вероятности называются априорными вероятностями. Возьмем случай полной («дурной») неопределенности, когда вероятности состояний природы либо вообще не существуют, либо не поддаются оценке даже приближенно. Обстановка неблагоприятна для принятия «хорошего» решения — попытаемся найти хотя бы не самое худшее. Здесь все зависит от точки зрения на ситуацию, от позиции исследователя, от того, какими бедами грозит неудачный выбор решения. Опишем несколько возможных подходов, точек зрения (или, как говорят, несколько «критериев» для выбора решения). Пусть имеется совокупность действий, операций а1, а2,..., аm, m ³ 2, (1) которые может совершить человек для достижения поставленной цели, причем одну и только одну операцию аi, iÎ{1, 2,..., m}, выбирает человек, принимающий решение. Кроме того, представлен перечень объективных условий, например, состояний природы Q1, Q2,..., Qn, (2) одно из которых Qj, jÎ{1, 2,..., n}, будет иметь место в действительности. Для каждой операции аi, i = 1, 2,..., m, при любом условии Qj, j = 1, 2,..., n, задана полезность (выгода, доход) в некоторых единицах aij. Величины aij, играющие роль платежей в теории игр, обычно задаются из эвристических, субъективных соображений. При этом возникают специфические трудности при их числовой оценке, обусловленные такими факторами, как: болезни, удовольствия, престиж, репутация и т.д. Величины aij можно задавать относительно, поэтому их называют показателями предпочтительности. Все перечисленные условия, при которых принимается решение, представлены в табл. 1.
Таблица 1
Если ЛПР не располагает никакой информацией о состояниях природы (2), то имеем ситуацию принятия решения в условиях полной неопределенности. Рассмотрим четыре известных подхода ПР в этой ситуации.
1.2. Максиминный критерий Вальда. Согласно этому критерию игра с природой ведется как игра с разумным, причем агрессивным противником, делающим все для того, чтобы помешать нам достигнуть успеха. Оптимальной считается стратегия, при которой гарантируется выигрыш в любом случае не меньший, чем «нижняя цена игры с природой». Для каждой операции аi, i = 1, 2,..., m, находим наихудший исход,
Затем определяется то значение i0, при котором величина
Принимаемое решение – выбор наилучшей операции
Рассмотренная операция максимин соответствует лучшему из худших исходов. Если руководствоваться этим критерием, олицетворяющим «позицию, крайнего пессимизма», надо, всегда ориентироваться на худшие условия, зная наверняка, что «хуже этого не будет». Критерий максимина является чисто перестраховочным, поскольку природа не может быть сознательным противником. Очевидно, такой подход - естественный для того, кто очень боится проиграть, - не является единственно возможным, но как крайний случай он заслуживает рассмотрения. Максиминную операцию использует только крайний пессимист, не желающий идти ни на какой риск. Обычно такие люди довольствуются малым и предпочитают спокойную жизнь.
1.3.Критерий минимакса сожалений Сэвиджа Этот критерий — тоже крайне пессимистический, но при выборе оптимальной стратегии советует ориентироваться не на выигрыш, а на риск. Выбирается в качестве оптимальной та стратегия, при которой величина риска (сожаления) в наихудших условиях минимальна. Сожаление (риска) в ТПР – потери в результате упущенных возможностей. Пусть природа находится в состоянии Qs найдем максимальный элемент s-го столбца табл. 1,
Мера сожаления определяется как разность:
где Для принятия решения к табл. 2 применяется критерий минимакса (minmax): для каждой операции ai, i=1,2,…, m, находится наибольшее сожаление,
Таблица 2
Затем среди членов последовательности
Последние два равенства соединим в одно:
Принимаемое решение – наилучшая операция Сущность такого подхода в том, чтобы всячески избегать большого риска при принятии решения. В смысле «пессимизма» критерий Сэвиджа сходен с критерием Вальда, но самый «пессимизм» здесь понимается по-другому.
1.4 Критерий равновозможных состояний (Лапласа) По этому критерию выбирается та операция ai0, для которой сумма полезностей
максимальна,
Задача. Рассмотрим на конкретном примере принятие решений по трем описанным критериям. Пусть m=3, n=2, и матрица полезностей представлена в табл. 3.
Таблица 3
Таблица 4
Например, ai – i-ый вариант технологического процесса для изготовления некоторых изделий, Q1 – возникновение дефицита в ближайшие два года на сырье, из которого изготовляются детали, Q2 – отсутствие такого дефицита. 1. Применяя операцию максимина, получим
Максиминной операцией является операция а2, гарантирующая 6 единиц полезности.
2. Для использования критерия минимакса сожалений необходимо для данных табл. 3 найти матрицу сожалений. Сначала находим максимальный элемент каждого столбца этой таблицы:
Тогда матрица сожалений примет вид, представленный в табл. 4. Применяя к данным этой таблицы критерий минимакса, получим: max(9, 3) = 9, max(0, 8) = 8, max(10, 0) = 10, min(9, 8, 10) = 8. Следовательно, операцией, соответствующей минимаксу сожалений, является операция а2. По критерию равновозможных состояний для данных табл. 3 имеем: Аi = 1+11 = 12, A2 = 10+6 = 16, A3 = 0+14 = 14,
Значит, оптимальной операцией по критерию равновозможных состояний природы является операция а2. В рассмотренном примере все три критерия дали один и тот же ответ: операция а2 является оптимальной, она гарантирует 6 ед. полезности. Если выбрать операцию а1, то в случае везения получим 11 ед. полезности, а в случае невезения – всего 1 ед. полезности. Если выбрать операцию а3, то в случае везения имеем 14 ед. полезности, а в случае невезения – 0 ед. полезности. Операция а2 гарантирует наибольшую полезность, 6 ед. Конкурирующие операции а1 и а3 гарантируют меньшие полезности: 1 ед. и 0 ед., соответственно.
Критерий Гурвица Этот критерий охватывает ряд различных подходов к принятию решений: от наиболее оптимистичного до наиболее пессимистичного. При наиболее оптимистичном подходе можно выбрать действие, дающее maxai maxq j { v(ai, q j) }. (Предполагается, что v(ai, q j) представляет выигрыш, или доход.) Аналогично при наиболее пессимистичных предположениях выбираемое действие соответствует maxai minq j { v(ai, q j) }. Критерий Гурвица устанавливает баланс между случаями крайнего оптимизма и крайнего пессимизма взвешиванием обоих способов поведения с соответствующими весами a и 1-a, где 0£a£1. Если v(ai, q j) представляет прибыль, то выбирается действие, дающее maxai {a maxq j v(ai, q j) + (1-a)minq j { v(ai, q j) }.В том случае, когда представляются затраты, критерий выбирает действие, дающее minai {a minq j v(ai, q j) + (1-a)maxq j { v(ai, q j) }.Параметр
ПРИМЕР: Одно из предприятий должно определить уровень предложенных услуг так, чтобы удовлетворить потребности клиентов в течении предстоящих праздников. Точное число клиентов не известно, но ожидается, что оно может принимать одно из четырех значений: 200, 250, 300 или 350 клиентов. Для каждого из этих возможных значений существует наилучший уровень предложения (с точки зрения возможных затрат). Отклонения от этих уровней приводят к дополнительным затратам либо из-за превышения предложения над спросом, либо из-за неполного удовлетворения спроса. Приводится таблица, определяющая потери в тысячах $.
Положим ниже. Оптимальное решение заключается в выборе
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 728; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.89.181 (0.012 с.) |

 . (3а)
. (3а) максимальна,
максимальна, . (3в)
. (3в) из множества исходных (1). Равенства (3а), (3в) можно объединить в одно
из множества исходных (1). Равенства (3а), (3в) можно объединить в одно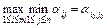 . (4)
. (4) .
.
 если
если  если
если  Тогда при состоянии природы Qs лучшей операцией является
Тогда при состоянии природы Qs лучшей операцией является  : для нее сожаление равно нулю. Изменяя последовательно значения s, s = 1,2,…, n, получим сожаление для каждой операции ai, i=1,2,…, m, при любом состояния природы Qs, s=1,2,…, n. Матрица сожалений представлена в табл. 2.
: для нее сожаление равно нулю. Изменяя последовательно значения s, s = 1,2,…, n, получим сожаление для каждой операции ai, i=1,2,…, m, при любом состояния природы Qs, s=1,2,…, n. Матрица сожалений представлена в табл. 2.
 , i=1,2,…, m, s = 1,2,…, n, находится минимальный
, i=1,2,…, m, s = 1,2,…, n, находится минимальный



 .
.



 .
. определяется как показатель оптимизма: при
определяется как показатель оптимизма: при 














