
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Многоэтапное принятие решенийСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Дерево решений
Многоэтапность приводит к тому, что схема принятия решения может быть представлена в виде дерева, в каждой вершине которого осуществляется либо: 1) Сознательный выбор между двумя и более альтернативами 2) Случайный переход из одной ветви в другую под воздействием внешних факторов Рассмотрим пример оптимизации многоэтапных решений на примере экономической задачи. Пример. Фирма может принять решение о строительстве крупного или мелкого предприятия. Строительство крупного предприятия относительно дешевле, в случае если будет высокий спрос на производимые товары, мелкое предприятие можно расширить. Деятельность фирмы рассматривается в течение десяти лет, причём в случае строительства мелкого предприятия, вопрос о расширении будет рассматриваться через два года. Спрос заранее неизвестен. Решение. Введём градацию спроса: высокий Расширенное предприятие в случае высокого спроса приносит доход – 900 тыс. $ в год, и при низком спросе – 200 тыс. $; мелкое предприятие без расширения при высоком спросе на производимый продукт приносит в течение двух лет по 250 тыс. $ ежегодно, а в течение следующих восьми по 200 тыс. $. Нарисуем наше дерево.
Применим для решения этой задачи метод динамического программирования. В качестве критерия применим средний выигрыш, т.е. МО выигрыша. Сама величина критерия равна доходу без затрат на строительство. Начнём с последнего четвёртого шага: подсчитаем средний выигрыш:
В данной задаче мы должны сделать два осознанных выбора. В первом случае мы видим, что выгодней не расширять мелкое предприятие через 2 года работы, в этом случае средний выигрыш будет выше на 300 тыс. Если выбирать между строительством крупного или мелкого предприятия, то оптимальным будем сразу строить крупное предприятие, в этом случае средний выигрыш составит 3,25 млн, тогда как при строительстве мелкого предприятия – 1,3 млн.
Решение задачи о секретарше.
Директор собирается принять на работу секретаршу. Прежний опыт делит секретарш на три категории: отличных (3 балла), хороших (2 балла) и посредственных (1 балл). Анализ учебных заведений по подготовке секретарш даёт статистику выпускниц заведений: вероятность взять на работу отличную секретаршу – 0,2, хорошую – 0,5, посредственную – 0,3. директор может испытать только трёх претенденток, причём в случае отказа директора кандидат убывает на другую работу. Построим дерево решений. Начнём искать оптимальное решение с последнего шага. Определим МО «выигрыша» секретарши, если мы испытываем трёх кандидаток:
Во втором испытании, если попалась хорошая секретарша, надо остановиться, а в первом испытании, надо остановиться только если попалась отличная, а в третье испытании берём любую. Найдём средний оптимальный выигрыш после всех испытаний: 2.2. Задания для самостоятельного решения Вариант 1 Вас пригласили на телевизионную игру Колесо фортуны. Колесо управляется электронным образом с помощью двух кнопок, которые сообщают колесу сильное (В) или слабое (Н) вращение. Само колесо разделено на равные области – белую (Б) и красную (К). Вам сообщили, что в белой части колесо останавливается с вероятностью 0,3, а в красной – 0,7. Плата, которую вы получаете за игру, равна (в рублях) следующему.
Изобразите соответствующее дерево решений. Вариант 2 Фермер Василий может выращивать либо кукурузу, либо соевые бобы. Вероятность того, что цены на будущий урожай этих культур повысятся, останутся на том же уровне или понизятся, равна соответственно 0.25, 0.30 и 0.45. Если цены возрастут, урожай кукурузы даст 3000000 рублей чистого дохода, а урожай соевых бобов – 1000000 рублей. Если цены останутся неизменными, Василий лишь покроет расходы. Но если цены станут ниже, урожай кукурузы и соевых бобов приведет к потерям в 2500000 и 500000 рублей соответственно. а) Представьте данную задачу в виде дерева решений. b) Какую культуру следует выращивать Василию?
Вариант 3 Допустим, у вас имеется возможность вложить деньги в три инвестиционных фонда открытого типа: простой, специальный (обеспечивающий максимальную долгосрочную прибыль от акций мелких компаний) и глобальный. Прибыль от инвестиции может измениться в зависимости от условий рынка. Существует 10%-ная вероятность, что ситуация на рынке ценных бумаг ухудшится, 50%-ная – что рынок останется умеренным и 40%-ная – рынок будет возрастать. Следующая таблица содержит значения процентов прибыли от суммы инвестиции при трех возможностях развития рынка.
а) Представьте задачу в виде дерева решений. b) Какой фонд открытого типа вам следует выбрать?
Вариант 4 Предположим, у вас имеется возможность вложить деньги в 7.5%-ные облигации, которые продаются по номинальной цене, либо в специальный фонд, который выплачивает лишь 1% дивидендов. Если существует вероятность инфляции, процентная ставка возрастет до 8%, и в этом случае номинальная стоимость облигаций увеличится на 10%, а цена акций фонда – на 20%. Если прогнозируется спад, то процентная ставка понизится до 6%. При этих условиях ожидается, что номинальная стоимость облигаций поднимется на 5%, а цена акций фонда увеличится на 20%. Если состояние экономики останется неизменным, цена акций фонда увеличится на 8%, а номинальная стоимость облигаций не изменится. Экономисты оценивают в 20% шансы наступления инфляции и в 15% - наступление спада. Ваше решение относительно инвестиций принимается с учётом экономических условий следующего года. а) Представьте задачу в виде дерева решений. b) Будете ли вы покупать акции фонда или облигации?
Вариант 5 Фирма планирует производство новой продукции питания. Исследовательский отдел убеждён в большом успехе новой продукции и хочет внедрить ее немедленно, без рекламной кампании на рынках сбыта фирма. Отдел маркетинга положение вещей оценивает иначе и предлагает провести интенсивную рекламную кампанию. Такая кампания обойдётся в 1 млн. рублей, а в случае успеха принесет 9,5 млн. рублей годового дохода. В случае неуспеха рекламной кампании (вероятность этого составляет 30%) годовой доход оценивается лишь в 2 млн. рублей. Если рекламная кампания не проводится вовсе, годовой доход оценивается в 4 млн. рублей при условии, что покупателям понравится новая продукция (вероятность этого равна 0.8), и в 2 млн. рублей с вероятностью 0.2, если покупатели останутся равнодушными к новой продукции. а) Постройте соответствующее дерево решений. b) Как должна поступить фирма в связи с производством новой продукции?
Вариант 6 Симметричная монета подбрасывается три раза. Вы получаете один рубль за каждое выпадение герба (Г) и дополнительно 25 копеек за каждые два последовательных выпадения герба (заметим, что выпадение ГГГ состоит из двух последовательностей ГГ). Однако Вам приходится платить 1.1 рубля за каждое выпадение решетки (Р). Вашим решением является участие или неучастие в игре. а) Постройте соответствующее дерево решений для описанной игры. b) Будете ли вы играть в эту игру?
Вариант 7 Предположим, у вас имеется возможность сыграть в игру следующего содержания. Симметричная игральная кость бросается два раза, при этом возможны четыре исхода: 1) выпадет два четных числа, 2) выпадет два нечетных числа, 3) выпадает сначала четное, затем нечетное число, 4) выпадает сначала нечетное, затем четное число. Вы можете делать одинаковые ставки на два исхода. Например, вы можете поставить на два четных числа (исход 1) и два нечетных числа (исход 2). Выигрыш на каждый рубль, поставленный на первый исход, равен 2 рубля, на второй и третий исходы – 1.95 рубля, на четвертый – 1.50 рубля. а) Постройте дерево решений для описанной игры. b) На какие исходы следует делать ставки? с) Можно ли иметь стабильный выигрыш в этой игре?
Вариант 8 Фирма имеет партии продукции с 0.8%, 1%, 1.2% и 1.4% бракованных изделий с вероятностями 0.4, 0.3, 0.25 и 0.05 соответственно. Три потребителя А, В и С заключили контракт на получение партий изделий с процентом некачественных изделий не выше 0.8%, 1.2% и 1.4% соответственно. Фирма штрафуется в сумме 2000 рублей за каждый пункт процента (пункт процента – это одна десятая процента) в случае, когда процент некачественных изделий выше указанного. Наоборот, поставка партий изделий с меньшим процентом бракованных изделий, чем оговорено в контракте приносит фирме прибыль в 1000 рублей за каждый пункт процента. Предполагается, что партии изделий перед отправкой не проверяются. а) Постройте соответствующее дерево решений. b) Какой из потребителей должен иметь наивысший приоритет при получении своего заказа?
Вариант 9 Фирма планирует открыть новое предприятие в Арканзасе. В настоящее время имеется возможность построить либо крупное предприятие, либо небольшое, которое через два года можно будет расширить при условии высокого спроса на выпускаемую им продукцию. Рассматривается задача принятия решений на десятилетний период. Фирма оценивает, что на протяжении этих 10 лет вероятность высокого и низкого спроса на производимую продукцию будет равна 0.75 и 0.25 соответственно. Стоимость немедленного строительства крупного предприятия равна 5 миллионов рублей, а небольшого – один миллион рублей. Расширение малого предприятия через два года обойдется фирме в 4.2 миллиона рублей. Прибыль, получаемая от функционирования производственных мощностей на протяжении 10 лет, приводится в следующей таблице.
а) Постройте соответствующее дерево решений, принимая во внимание, что через два года фирма может либо расширить небольшое предприятие, либо не расширять его. b) Сформулируйте стратегию строительству для фирмы на планируемый 10-летний период. (Для простоты не принимайте во внимание возможную инфляцию.)
Вариант 10 Решите упр.9 в предположении, что спрос может быть высоким, средним и низким с вероятностями 0.7, 0.2 и 0.1 соответственно. Расширение небольшого предприятия будет проведено лишь в том случае, если на протяжении первых двух лет спрос будет высоким. Следующая таблица содержит данные о прибылях за год.
НЕЧЕТКИЕ МНОЖЕСТВА 3.1 Основные определения Необходимость введения нечетких множеств (НМ) обоснована тем, что по мере роста сложности систем падает наша способность делать точные и значащие утверждения относительно поведения системы. Пусть U – универсальное множество объектов; A – конечное размытое подмножество U и A = {ui; m (ui)}, где ui Î U, и m (ui) – мера членства, которая указывает степень принадлежности к множеству U. Если m (ui) = {0,1}, то m (ui) – обычная булева функция. Лингвистические переменные “верно”, “совершенно верно”, “не вполне верно” могут рассматриваться как метки размытых множеств.
Таблица 1
Таблица 2. Пример 1: Понятие «высокий».
Отличие mA (ui) от функции распределения случайной велечины: m -функция, определяющая субъективное мнение специалиста, а функция распределения – это объективный закон, независимый от отношения специалиста к этому явлению. Определение: P(X1, ….,Xn) ® B - предикат, где B – множество булевых переменных. Определение: j~ = (X, F~) – нечеткое отношение, где X – множество, F~ – нечеткое подмножество X2. X – область задания, F~- нечеткий график отношения. Способы задания отношений – теоретико-множественный, матричный, графический и с помощью нечетких предикатов. 1. Теоретико-множественный: перечисление X= {Xi} и задание F~ = {mF (xi, xj), (xi, xj)}, где (xi, xj)ÎX2. 2. Матричный: задается матрица смежности Rj, где на пересечении i-ой строки и j – го столбца стоит rij = mF (xi, xj). 3. Можно задать j~ в виде графа с множеством вершин X, дугами (xi, xj), которым приписано mF (xi, xj). 4. j~ = (X, F~) – нечеткое отношение, если mF (a,b) Î F; a,b Î X, то a j~ b – нечеткое логическое высказывание, значение истинности которого mF (a,b). Пример 2: Теоретико-множественное задание отношения “любит”. Таблица 3
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 3928; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.126.69 (0.011 с.) |

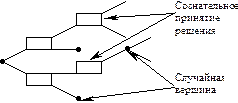
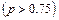 и низкий
и низкий 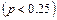 . Затраты и доходы: строительство крупного предприятия – 5 млн. $; строительство мелкого – 1 млн. $; затраты на расширение – 4,2 млн. $; крупное предприятие при высоком спросе даёт доход – 1 млн. $ ежегодно, а при низком – 300 тыс. $; мелкое предприятие при высоком спросе – 250 тыс. $ ежегодно, при низком – 200 тыс. $.
. Затраты и доходы: строительство крупного предприятия – 5 млн. $; строительство мелкого – 1 млн. $; затраты на расширение – 4,2 млн. $; крупное предприятие при высоком спросе даёт доход – 1 млн. $ ежегодно, а при низком – 300 тыс. $; мелкое предприятие при высоком спросе – 250 тыс. $ ежегодно, при низком – 200 тыс. $.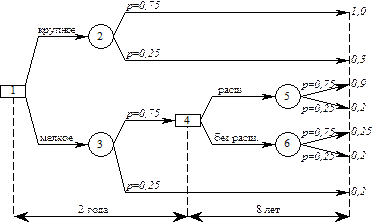


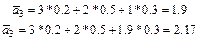
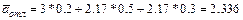 .
.


