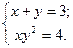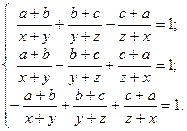Решение уравнений и их систем – команда solve

 

Для решения систем уравнений и одиночных уравнений служит команда

solve(expr1, expr2,..., exprN, var1, var2,..., varN). Она возвращает значения переменных varI, при которых соблюдаются равенства, заданные выражениями exprI. Если в выражениях не используются знаки равенства, то полагается, что exprI = 0.

Результат может быть возвращен в следующих формах:

для одного уравнения и одной переменной решение возвращается в виде одномерного или многомерного массива ячеек;

при одинаковом числе уравнений и переменных решение возвращается в упорядоченном по именам переменных виде.

Команда solve позволяет найти не только вещественные, но и комплексные решения систем уравнений и одиночных уравнений. Справку по этой команде можно получить, введя команду doc solve.

Пример:

Решить уравнение x³ - 1 = 0.

Решение:

>> syms x,y=x^3-1;S=solve(y)

S =

[ 1]

[ -1/2+1/2*i*3^(1/2)]

[ -1/2-1/2*i*3^(1/2)]

В результате получены три разных значения корня x₁ = 1, x₂ =, x₃ =, которые хранятся соответственно в элементах S(1), S(2), S(3) массива S.

С помощью subs (разд. 7.7) подставим найденные значения корней в выражение x³ - 1:

>> subs(y,x,S)

ans =

[ 0]

[ (-1/2+1/2*i*3^(1/2))^3-1]

[ (-1/2-1/2*i*3^(1/2))^3-1]

>> [m]=simple(ans)

m =

[ 0]

[ 0]

[ 0]

Выражение x³ - 1 принимает значение 0 при подстановке любого из найденных корней, поэтому x₁, x₂, x₃ являются точными корнями уравнения x³ - 1 = 0.

Команда roots (см. разд. 6.1) нашла бы только приближенные значения корней уравнения x³ - 1 = 0. В общем случае полиномиальное уравнение степени выше 4 не может иметь точного решения, выраженного с помощью радикалов.

Команда solve позволяет решать уравнения, представленные в аналитическом виде.

Пример:

Решить квадратное уравнение ax²+bx+c = 0.

Решение:

>> S=solve('a*x^2+b*x+c=0',x)

S =

[ 1/2/a*(-b+(b^2-4*a*c)^(1/2))]

[ 1/2/a*(-b-(b^2-4*a*c)^(1/2))]

Команда solve возвратила известные выражения корней x_1,2 = квадратного уравнения ax²+bx+c = 0. Точно также можно выразить с помощью радикалов решения кубического уравнения ax³+bx²+cx+d = 0, хотя эти выражения достаточно сложные.

Пример:

Решить трансцендентное уравнение x^lnx+1 - 1 = 0.

Решение:

>> syms x

>> S=solve('x^(log(x)+1)-1',x)

S =

[ exp(0)]

[ exp(-1)]

Проверка:

>> subs(x^(log(x)+1)-1,x,S)

ans =

[ 0]

[ 0]

В данном случае solve нашла точные значения корней x₁ = 1, x₂ = e⁻¹.

Пример:

Решить трансцендентное уравнение lnx + 3 - x = 0.

Решение:

>> solve('log(x)+3-x=0')

ans =

[ -lambertw(-exp(-3))]

[ -lambertw(-1,-exp(-3))]

Команда solve возвратила значения корней, выраженные через функцию Ламберта.

Команда vpa возвращает приближенные значения этих корней, вычисленные с 20 значащими цифрами:

>> vpa(ans,20)

ans =

[.52469097457714872410e-1]

[ 4.5052414957928833670]

Каждый из приближенных корней этого уравнения был найден по отдельности в разделе 6.2 с помощью команды fzero. Отметим, что команда solve нашла приближенные значения двух корней одновременно с высокой точностью. При этом не пришлось графически определять интервалы изоляции корней.

Решение любого трансцендентного уравнения, в том числе и тригонометрического (разд. 7.17), достаточно сложная и серьезная проблема. Иногда solve возвращает неверные решения.

Пример:

Решить трансцендентное уравнение sinx^lnsinx+x^x - 2 = 0.

Решение:

>> syms x

Y=sin(x)^log(sin(x))+x^x-2;

>> S=solve(Y)

S =

1/2*pi

>> subs(Y,S)

ans =

-1+(1/2*pi)^(1/2*pi)

>> vpa(ans,5)

ans =

1.0327

Найденное решение неверное, т. к. оно не прошло проверку подстановкой.

Команда solve может возвратить не все решения.

Пример:

Решить трансцендентное уравнение sinx+lnx+e^x - 1 = 0.

Решение:

>> syms x

>> Y=sin(x)+log(x)+exp(x)-1;

>> S=solve(Y);

>> vpa(S,5)

ans =

-3.0553-1.7145*i

>> subs(Y,S)

ans =

-.8e-31-.1e-30*i

Возвратив приближенный комплексный корень уравнения x₁ = -3,0553 - 1,7145i, solve не нашла вещественный корень. С помощью команды ezplot (разд. 7.16) графически определяем, что он находится вблизи значения 0,4 (рис. 7.2):

>> ezplot('sin(x)+log(x)+exp(x)-1',[0,1,-1, 3])

>> grid

 

 

Рис.7.2

Вещественный корень со стартовым приближением 0,4 найдем с помощью команды fzero (разд. 6.2):

>> format long

>> [X,f]=fzero('sin(x)+log(x)+exp(x)-1',0.4)

X =

0.40716029855672

f =

-2.220446049250313e-016

Итак, приближенное значение вещественного корня x₂=0,4072.

Перейдем теперь к системам уравнений.

Пример:

Решить систему уравнений

 

 

Решение:

Результатом выполнения команды solve является структура S с полями x и y, каждое из которых содержит символьное представление решения:

>> syms x y

>> Y1=x+y-3;

>> Y2=x*y^2-4;

>> S=solve(Y1,Y2,x,y)

S =

x: [3x1 sym]

y: [3x1 sym]

Выведем в командное окно содержимое структуры:

disp([S.x S.y])

[ 4, -1]

[ 1, 2]

[ 1, 2]

Получили три решения (x₁;y₁) = (4; -1) и (x₂;y₂) = (1;2) (второе – кратности 2), причем (x₁;y₁) хранится в [S.x(1) S.y(1)], а (x₂;y₂) – в [S.x(2) S.y(2)]:

>> disp([S.x(1) S.y(1)])

[ 4, -1]

>> disp([S.x(2) S.y(2)])

[ 1, 2]

Для проверки подставим в выражения Y1 = x+y - 3 и Y2 = xy² - 4 вначале первое решение, а затем второе:

>> disp(subs([Y1 Y2],[x y],[S.x(1) S.y(1)])

[ 0, 0]

>> disp(subs([Y1 Y2],[x y],[S.x(2) S.y(2)])

[ 0, 0]

Как видим, найдены точные решения, т. к. выражения Y1 и Y2 при их подстановке обратились в 0.

Команда solve допускает использование символьных переменных в качестве выходных аргументов. Эквивалентное обращение к solve в предыдущем примере имеет вид:

>> [x,y]=solve(Y1,Y2,x,y)

x =

[ 4]

[ 1]

[ 1]

y =

[ -1]

[ 2]

[ 2]

Команда solve позволяет решать системы уравнений, заданные в аналитическом виде.

Пример:

Решить систему уравнений относительно x, y, z

 

 

Решение:

>> syms a b c x y z

>> Y1=(a+b)/(x+y)+(b+c)/(y+z)-(c+a)/(z+x)-1;

>> Y2=(a+b)/(x+y)-(b+c)/(y+z)+(c+a)/(z+x)-1;

>> Y3=-(a+b)/(x+y)+(b+c)/(y+z)+(c+a)/(z+x)-1;

>> S=solve(Y1,Y2,Y3,x,y,z)

S =

x: [1x1 sym]

y: [1x1 sym]

z: [1x1 sym]

>> disp([S.x S.y S.z])

[ a, b, c]

Проверим найденное решение (a;b;c) подстановкой в систему:

>> subs([Y1 Y2 Y3],[x y z],[S.x S.y S.z])

ans =

[ 0, 0, (-a-b)/(a+b)+1]

>> disp(simplify(ans))

[ 0, 0, 0]

Убеждаемся, что решение найдено верно.

Иногда системе MATLAB можно помочь, преобразовав уравнение или систему уравнений к эквивалентному виду.

Например, уравнение ln(4 - 2x)+x² - 2 = 0 имеет эквивалентный вид e^2−x²+2x - 4 = 0. Можно проверить, что для каждого из этих уравнений команда solve возвращает свой вещественный корень. Это будут разные корни, но каждый из них удовлетворяет исходному уравнению. Существует и третий вещественный корень, который можно найти с помощью команды fzero.

Пример:

Решить систему трансцендентных уравнений

 

 

Решение:

>> syms x y

>> Y1=3^y*9^x-81;

>> Y2=log10((y+x)^2)-log10(x)-2*log10(3);

>> S=solve(Y1,Y2,x,y)

S =

x: [4x1 sym]

y: [4x1 sym]S =

>> R=[S.x S.y];

>> disp(vpa(R,10))

[ 16.00000002, -28.00000004]

[ 16.00000002, -3.999999992]

[ 1.000000000, -3.999999996]

[ 1.000000000, 1.999999996]

Получили 4 приближенных решения c 10 значащими цифрами. Однако системе удовлетворяют только первое и последнее из них. Убедимся в этом подстановкой:

>> disp(vpa(subs([Y1,Y2],[x y],[S.x(1) S.y(1)]),15))

[.1e-12,.15e-13]

>> disp(vpa(subs([Y1,Y2],[x y],[S.x(2) S.y(2)]),15))

[ 22876792454891.6,.25e-13]

>> disp(vpa(subs([Y1,Y2],[x y],[S.x(3) S.y(3)]),15))

[ -80.8888888888889,.31e-13]

>> disp(vpa(subs([Y1,Y2],[x y],[S.x(4) S.y(4)]),15))

[ -.71e-11,.18e-13]

Приближенное равенство [Y1,Y2]» [0,0] выполняется только при подстановке в систему первого и последнего решений. В остальных случаях [Y1,Y2] ≠ [0,0].

Алгебраическими преобразованиями приведем исходную систему к эквивалентной системе

 

 

Решим ее:

>> syms x y

>> S=solve('y+2*x=4','(y+x)^2/x=9',x,y);

>> [S.x S.y]

ans =

[ 1, 2]

[ 16, -28]

Получили два точных решения, являющихся также решениями исходной системы.

Пример:

Решить cистему нелинейных уравнений

 

 

Решение:

>> syms x y z

>> Y1=x+x^2-2*y*z-.1;

>> Y2=y-y^2+3*x*z+.2;

>> Y3=z+z^2+2*x*y-.3;

>> S=solve(Y1,Y2,Y3,x,y,z);

>> R=[S.x S.y S.z];

>> disp(vpa(R,6))

[ -.541941+.626019e-1*i, -.179057-.433417*i,.148543-.344892*i]

[ -.541941-.626019e-1*i, -.179057+.433417*i,.148543+.344892*i]

[.128241e-1, -.177801,.244688]

[ -1.08804, -.130325,.161425e-1]

[.578802e-1,.156279e-1, -1.24040]

[.374678+.356411*i,.353227-.580416*i, -.281751+.419593*i]

[.374678-.356411*i,.353227+.580416*i, -.281751-.419593*i]

[.121093, 1.17493,.152166e-1]

Получено 8 приближенных решений с 6 значащими цифрами, 4 из которых вещественные (c 3 - го по 5 - е и 8 - е). В разделе 6.2 командой fsolve было найдено 4 - е решение. Проверим все 8 решений подстановкой с помощью цикла for:

>> for i=1:8

T=subs([Y1 Y2 Y3],[x y z],[S.x(i) S.y(i) S.z(i)]);

disp(vpa(T,6))

end

[ -.5e-31-.1471e-30*i, -.32e-30+.71e-30*i,.25e-30+.103e-29*i]

[ -.5e-31+.1471e-30*i, -.32e-30-.71e-30*i,.25e-30-.103e-29*i]

[.12e-30,.9e-31, -.13e-30]

[.8e-31,.14e-30, -.3e-31]

[.2e-31, -.6e-31, -.14e-30]

[.637e-29+.829e-29*i, -.754e-29+.15e-30*i,.709e-29-.346e-29*i]

[.637e-29-.829e-29*i, -.754e-29-.15e-30*i,.709e-29+.346e-29*i]

[.17422e-27, -.1012e-28,.12735e-27]

При подстановке любого из решений [Y1 Y2 Y3]» [0 0 0]. Значит, каждое из них удовлетворяет системе уравнений.