
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оператор переключения switchСодержание книги
Поиск на нашем сайте
Ход работы программы может определяться значением некоторой переменной (переключателя). Такой альтернативный способ ветвления программы основан на использовании оператора переключения switch. Переменная-переключатель помещается после switch через пробел. Оператор switch содержит наборы команд, начинающиеся со слова case. После каждого case через пробел записывается то значение переключателя, при котором выполняется данный набор. Последний набор начинается со слова otherwise, его команды выполняются в том случае, когда ни один из наборов case не был выполнен. Если хотя бы один из наборов case выполнен, то происходит выход из оператора switсh и переход к команде, следующей за end. Предположим, что требуется найти количество единиц и минус единиц в заданном массиве и, кроме того, найти сумму всех элементов, отличных от единицы и минус единицы. Создадим файл-функцию, которая по заданному массиву возвращает число минус единиц в первом выходном аргументе, число единиц – во втором, а сумму – в третьем. В ней следует перебрать все элементы массива в цикле, причем в роли переменной-переключателя будет выступать текущий элемент массива: function [m,p,s]=mpsum(x) m=0; p=0; s=0; for i=1:length(x) switch x(i) case -1 m=m+1; case 1 p=p+1; otherwise s=s+x(i); end end Набор case может быть выполнен не только при одном определенном значении переключателя, но и в том случае, когда переключатель принимает одно из нескольких допустимых значений. В этом случае значения указываются после слова case в фигурных скобках через запятую, например, case {1,2,3}. Оператор прерывания цикла break
Досрочное завершение циклов while или for осуществляется при помощи оператора break. Пусть, например, требуется по заданному массиву x образовать новый массив y по правилу y(k) = x(k+1)/x(k) до первого нулевого элемента x(k), т. е. до тех пор, пока имеет смысл операция деления. Номер первого нулевого элемента в массиве x заранее неизвестен, более того, в массиве x может и не быть нулей. Решение задачи состоит в последовательном вычислении элементов массива y и прекращении вычислений при обнаружении нулевого элемента в x. Следующая файл-функция демонстрирует работу оператора break: function y=div(x) for k=1:length(x)-1 if x(k)==0 break end y(k)=x(k+1)/x(k); end Справку по разделам 4.2 – 4.5 можно получить с помощью команды doc lang. Пример сравнения быстродействия матричных и скалярных операций
За умножением векторов и матриц в смысле линейной алгебры в MATLAB закреплен знак <*>. Определение произведения прямоугольных матриц дано в разделе 1.10. Пример умножения матриц в матричной форме с помощью знака <*>: >> A=ones(3) A = 1 1 1 1 1 1 1 1 1 >> B=ones(3) B = 1 1 1 1 1 1 1 1 1 >> C=A*B C = 3 3 3 3 3 3 3 3 3 В традиционных языках программирования умножение матриц в смысле линейной алгебры осуществляется в скалярной форме с помощью вложенных циклов. Ниже приведен текст файл-функции умножения матриц D и E размера n×n в скалярной форме: function G=Matr(D,E,n) for i=1:n for j=1:n s=0; for k=1:n s=s+D(i,k)*E(k,j); end G(i,j)=s; end end Сохраним этот текст в Matr.m. Теперь с помощью файл-функции Matr.m скалярное умножение матриц А и В можно реализовать следующим образом: >> A=ones(3);B=ones(3); >> Matr(A,B,3) ans = 3 3 3 3 3 3 3 3 3 В этом примере умножение матриц осуществлено в скалярной форме. Результаты умножения матриц в матричной и скалярной формах совпадают. Сравним теперь быстродействие обеих форм умножения матриц с помощью набора команд tic и toc (см. разд. 1.7). Найдем оценку времени выполнения файл-функции Matr.m: >> A=ones(3);B=ones(3); >> tic,Matr(A,B,3);toc elapsed_time = Найдем теперь оценку времени умножения этих же матриц А и B в матричной форме: >> tic,A*B;,toc elapsed_time = Так как матрицы А и В имеют небольшой размер 3×3, то оценочное время выполнения умножения в обеих формах практически равно нулю. Проведем теперь сравнение по быстродействию операции умножения матриц А и В размером 1000×1000 с использованием этой операции в скалярной и в матричной формах: >> A=ones(1000);B=ones(1000); >> tic,Matr(A,B,1000);,toc elapsed_time = 313.9780 >> tic,A*B;toc elapsed_time = 8.5320 Следовательно, умножение в матричной форме матриц А и В размером 1000×1000 осуществляется в MATLAB примерно в ≈ 37 раз быстрее, чем в скалярной форме (независимо от быстродействия компьютера). В рассмотренных примерах использованы матрицы c единичными элементами. Это связано с простотой генерации матриц. Матрицы А и В автоматически созданы командой ones (см. разд. 2.4). Теперь создадим матрицы со случайными значениями элементов. Для этого используем встроенный генератор rand (см. разд. 2.4) равномерно распределенных случайных чисел. Оценка времени, которое затрачивается на выполнения их умножения в матричной форме составляет: >> A=rand(1000);B=rand(1000); >> tic,A*B;,toc elapsed_time = 8.7530 Результат 8,75 с. практически такой же, как и для матриц c единичными элементами того же размера (8,53 с.). Вывод: Там, где это возможно, вместо операторов цикла лучше применять матричные операции над массивами, которые исполняются в MATLAB намного быстрее. Вопросы для самопроверки 1. Какие операции отношения определены над числами в MATLAB? 2. Какие логические операции над вещественными числами определены в MATLAB? 3. Какова иерархия приоритетов в выполнении математических операций, операций отношения и логических операций? 4. Как работают циклы for, while? 5. Как используется конструкция if-elseif-else для изменения хода программы в зависимости от нескольких условий? 6. Как работают операторы switch, break?
ГЛАВА 5 ВЫСОКОУРОВНЕВАЯ ГРАФИКА Одна из задач этого пособия состоит в том, чтобы помочь читателю в приобретении основных навыков по формированию графических моделей разнообразных функций, объясняющих математические зависимости, а также иллюстрирующих физические, химические, электромагнитные и др. процессы. Применение компьютерной графики часто оказывается полезным не только для наглядного представления результатов вычислений, но для отладки инженерных и научных программ. Предполагается, что для понимания дальнейшего материала читатель знаком с интерфейсомMATLAB, а также имеет необходимый минимум знаний по работе с М-файлами, массивами чисел и их элементами, а также программированию и отладке программ в этой среде. Высокоуровневая графика позволяет пользователю получать результаты в графическом виде, прикладывая минимум усилий. Основную работу, связанную с построением графика, масштабированием осей, подбором цветов, а в случае 3 -х мерной графики и с углом обзора наблюдаемого объекта берет на себя средаMATLAB. В настоящей главе приводятся сведения, необходимые для построения графиков следующих типов: графики на плоскости в декартовой системе координат; трехмерные графики функций двух переменных в декартовой системе координат и особенности их построения. Отдельно рассмотрены вопросы оформления графиков, их сохранения и экспорта, а также элементы анимации. При создании с помощью компьютера графика той или иной зависимости необходимо иметь в виду, что компьютер способен работать только с числами, но не с непрерывными значениями аргументов и их функций. Поэтому, если порой наблюдателю кажется, что график той или иной функции представлен на экране монитора плавными кривыми или объемными телами, то это всего лишь иллюзия. Такая иллюзия достигается благодаря тому, что между отдельными значениями аргументов и их функций выбран достаточно малый интервал, а также тем, что современные мониторы и принтеры обладают настолько высокой разрешающей способностью, что глаз человека не способен воспринимать имеющиеся неоднородности в графической модели. Если этот интервал увеличить, то на графике функции будут видны изломы. При чтении материала следует иметь в виду, что серый цвет в текстах программ использован для выделения фрагментов, которые содержат операторы вывода графиков, специальные команды, позволяющие менять способ их визуализации и команды по оформлению графиков. D графика
Под 2D графикой будем понимать визуализацию результатов вычислений путем построения графических зависимостей на плоскости в декартовой (прямоугольной) или полярной системе координат. Дальнейший материал ограничен рассмотрением только декартовой системы координат, как наиболее часто применяемой при решении практических задач. При этом возможно построение графиков функций одной переменной или графиков функций, заданных параметрически, т. е. двумя уравнениями х(t) и у(t) при изменении t в заданных пределах. При графической визуализации параметрически заданных функций вначале для одинаковых значений t вычисляются значения функций х(t) и у(t), а затем строится график зависимости у(х). Читатель должен знать, что главным условием создания и визуализации графических зависимостей в MATLAB является четкое понимание того, как в этой среде осуществляются поэлементные операции с векторами. Графики в линейном масштабе
Построение графика функции одной переменной (или нескольких таких графиков) в линейном масштабе осуществляется с помощью команды plot(…). Рассмотрим использование команды plot(…) на конкретных примерах. Пример 1. Построить график функции y(t) = e-2tcos(10t), где аргумент t меняется в интервале [0;1] с шагом 0,01 (рис. 5.1). >> t=[0:0.01:1]; >> y=exp(-2*t).*cos(10*t); >> plot(t,y)
Рис. 5.1 Пример 2. Построить в одном окне графики двух функций x(t) = 2sin(50t) и y(t)=e-2tcos(10t), где аргумент t меняется в интервале [0;2] с шагом 0,01, (рис. 5.2). >> t=[0:0.01:2]; >> y=exp(-2*t).*cos(10*t); >> x=2*sin(50*t); >> plot(t,x,t,y)
Рис. 5.2 Обсудим построенные графики. 1. Команда plot(t,x) позволяет строить в декартовой системе координат график одномерной функции x с аргументом t. При этом в скобках на первом месте стоит аргумент, а на втором функция. 2. MATLAB (если это не указано специально) самостоятельно выбирает цвет графика, масштаб и оцифровывает оси абсцисс и ординат. Из рис. 5.2 видно, что масштабирование производится по максимальным значениям одной из функций и ее аргумента. 3. Для функции x(t) = 2sin(50t) шаг изменения аргумента оказался не достаточно малым, и поэтому на ее графике отчетливо видны изломы. Порой неверный выбор шага изменения аргумента функции может существенно исказить ее график. Если пользователь затрудняется выбрать подходящий шаг (шаг дискретизации аргумента), то при выводе графика функции можно воспользоваться командой fplot(…), и MATLAB подберет шаг дискретизации самостоятельно. Поясним это на примере. Пусть требуется вычислить функцию y = cos10x·(sinx+0,1sin(100πx)) на интервале [0;1]. Если шаг дискретизации Δх выбрать равным Δх = 0.01, то при выводе графика с помощью команды plot(…) получим результат, показанный на рис. 5.3а, что не соответствует истинной картине. Дело в том, что при таком шаге второе слагаемое сомножителя, заключенного в скобки, все время обращается в нуль. Верен график, показанный на рис. 5.3б. Листинги программ вычисления функции и вывода ее графика с помощью команды plot(…) и команды fplot(…) выглядят следующим образом: Вариант с применением Вариант с применением команды plot(…) (рис. 5.3а) команды fplot(…) (рис. 5.3б) x=[0:0.01:1]; y=myfun(x); y=cos(10*x).*(sin(x)+0.1*sin(100*pi*x)); fplot(‘myfun’,[0,1]) plot(x,y)
Рис. 5.3а Рис. 5.3б Первым входным аргументом fplot(…) является имя файл-функции, а вторым – вектор, элементы которого есть границы отрезков: fplot('имя файл-функции', [a,b]). Для приведенного примера файл-функция myfun имеет вид: function y=myfun(x); y=cos(10*x).*(sin(x)+0.1*sin(100*pi*x)); Иногда требуется сравнить поведение двух функций, значения которых сильно отличаются друг от друга. При этом на графике с небольшими значениями функции бывает трудно выявить ее характерные особенности. В таком случае можно воспользоваться командой plotyy(…), который позволяет вывести графики двух функций в одно окно и нанести в этом окне две оси ординат, имеющие подходящий масштаб. Пример 3. Увеличим амплитуду синусоиды функции x(t) из примера 2 в 50 раз, т.е. положим что x(t) = 100sin(50t), а y(t) = e-2tcos(10t), где аргумент t меняется от 0 до 2 с шагом 0,01. Если для построения графиков этих функций использовать команду plot(…), то получим график, представленный на рис. 5.4
Рис. 5.4 Выведем теперь графики тех же функций с помощью команды plotyy(…) (рис. 5.5)
Рис. 5.5 На рис. 5.5 проявляются характерные особенности каждой из функций. Кроме того, на цветном мониторе видно, что цвет каждой из вертикальных осей повторяет цвет соответствующего графика. При черно-белом изображении графики различных функций отличаются лишь оттенками серого цвета. Иногда график функции требуется снабдить заранее заданными отличительными признаками, например, цветом, определенным типом линии, расположить на этой линии специальные символы (маркеры). Для этого также применяется команда plot(…), но более сложной конструкции. Пример 4. Вычертить график функции y(t) = e-2tcos(10t) в виде штриховой линии красного цвета, помеченной маркером типа «кружок». Аргумент t меняется в интервале [0;1] с шагом 0,03. Эта задача решается следующим образом (рис. 5.6): >> t=[0:0.03:1]; >> y=exp(-2*t).*cos(10*t); >> plot(t,y,'ro--')
Рис. 5.6 Полезно сравнить структуру команды plot(…) в этом примере и в примере 1. Из сравнения следует, что в команду plot(…) в настоящем примере включен дополнительный параметр, который заключается в апострофы. Этот параметр представляет собой последовательность символов, определяющих цвет линии (r – это красный цвет), тип маркера (о – это кружок) и стиль линии (двойной дефикс, т.е. символ -- соответствует штриховой линии). Заметим, что внутри апострофов между отдельными символами нет никаких разделительных знаков. В таблице 5.1 содержатся данные, необходимые для определения свойств линий графиков.
Таблица 5.1 Свойства графиков
Команда plot(t,y,S), где S – дополнительный параметр, заключенный в апострофы [например, у +- (цвет желтый, тип маркера +, стиль линии сплошная) или сd: (голубой, ромб, пунктирная) или другая комбинация символов из табл 5.1], чаще всего применяется вычерчивании нескольких графиков в одном окне. Поясним это на примере. Пример 5. Вычертить в одном окне графики трех функций y >> t=[-2*pi:0.1*pi:2*pi]; >> y1=sin(0.5*t); >> y2=cos(0.5*t); >> y3=sin(t).^5; >> plot(t,y1,'k',t,y2,'r-.+',t,y3,'-o')
Рис. 5.7 В данном случае команда plot(…) содержит требования по выводу графиков трех функций: у1, у2 и у3. При этом параметр S для функции у1 состоит лишь из двух символов. В этом случае S = ’-m'. В то же время для функции у2S = '-.+r', а для функции у3S = '-ok'. Вывод: Символы, определяющие цвет, тип маркера, стиль линии и находящиеся внутри апострофов, могут располагаться в любой последовательности. Внутри апострофов могут располагаться один, два или три таких символа. В заключение рассмотрения команды plot(…) отметим, что она может использоваться и с одним аргументом, например, в виде plot(Y). При этом аргумент команды plot(…), т. е. Y, должен быть предварительно задан в виде вектора или матрицы. Если Y есть вектор, то на графике строится зависимость значений элементов вектора от номеров элементов. Если аргументом команды plot(…) является матрица, то на одни координатные оси выводятся графики столбцов. Пример 6. Построить график функции y(t) = e-2tcos(10t), где аргумент t меняется от 0 до 1 с шагом 0,01. Функцию у задать как вектор. >> t=[0:0.01:1]; >> Y=exp(-2*t).*cos(10*t); >> plot(Y) В результате выполнения программы построенный график (рис. 5.8) по форме повторяет график, представленный на рис. 5.1. Однако, разбиение оси абсцисс на рис. 5.8 производится по возрастанию номеров элементов вектора Y. Номера элементов вектора – всегда целые числа.
Рис. 5.8 Пример 7. Применить команду plot для построения в одном окне графиков столбцов матрицы Y (рис. 5.9). >> t=[0:0.2*pi:pi]; >> fi=0:0.2*pi:pi; >> Y=(cos(t)).^2+sin(fi); >> plot(Y)
Рис. 5.9
|
|||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 439; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.013 с.) |








 (t) = sin(0,5t), y
(t) = sin(0,5t), y 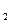 (t) = cos(0,5t) и y
(t) = cos(0,5t) и y  (t) = sin
(t) = sin  t при изменении t в пределах от – 2π до 2π с шагом 0,1π (рис. 5.7).
t при изменении t в пределах от – 2π до 2π с шагом 0,1π (рис. 5.7).





