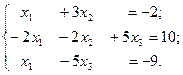Решение систем линейных уравнений

 

MATLAB позволяет работать с объектами линейной алгебры, т. е. векторами и матрицами, настолько просто, насколько это вообще возможно.

Яркий пример этому – решение систем линейных уравнений.

Пример:

Пусть дана система линейных уравнений

 

 

Решить систему с применением оператора обратного деления матриц < \ >.

Решение:

В матричной записи система имеет вид Ах = b, где

 

A =, b =, х =

 

– соответственно матрица из коэффициентов при незвестных, вектор-столбец из свободных членов и вектор-столбец из неизвестных.

Введем матрицу А и вектор-столбец свободных членов b:

>> А=[1 3 0;-2 -2 5;1 0 -5]

А =

1 3 0

-2 -2 5

1 0 -5

>> b=[-2;10;-9]

b =

-2

-9

Известно, что система имеет единственное решение, если определитель матрицы А не равен нулю (│ A │ = det(A) ≠ 0). Вычислим определитель матрицы А:

>> disp(det(A))

-5

Определитель не равен нулю. Находим решение системы с помощью оператора обратного деления матриц < \ >:

>> x=А\b

x =

-1

Проверим полученное решение x₁ = 1, x₂ = -1, x₃ = 2 подстановкой в систему уравнений:

>> disp(A*x)

-2.0000

10.0000

-9.0000

В результате проверки получен вектор-столбец свободных членов. Значит, система решена верно.

Найдем теперь решение системы х = A^-1b с помощью обратной матрицы. Вначале вычислим обратную матрицу A^-1:

>> A1=inv(A)

A1 =

-2.0000 -3.0000 -3.0000

1.0000 1.0000 1.0000

-0.4000 -0.6000 -0.8000

Находим решение системы:

>> A1*b

ans =

1.0000

-1.0000

2.0000

Отметим, что решение системы с помощью обратной матрицы требует больше времени и памяти, к тому же этот способ может дать большую погрешность решения. Поэтому для решения линейных систем рекомендуется применять оператор обратного деления < \ >.

Пример:

Решить систему линейных уравнений

 

 

Решение:

>> A=[1 3 0;-2 -2 5;1 0 5]

A =

1 3 0

-2 -2 5

1 0 5

>> b=[-2 10 -9]

b =

-2 10 -9

>> disp(det(A))

Находим решение системы:

>> x=A\b'

x =

-7.5714

1.8571

-0.2857

Заметим, что обратное деление произведено на вектор-столбец b', поскольку вектор b введен как вектор-строка. Получили приближенное решение системы. Вычислим обратную матрицу A^-1:

>> disp(inv(A))

-0.2857 -0.4286 0.4286

0.4286 0.1429 -0.1429

0.0571 0.0857 0.1143

Точное решение системы и точная обратная матрица выражаются через рациональные дроби:

>> format rat

>> x=A\b'

x =

-53/7

13/7

-2/7

>> disp(inv(A))

-2/7 -3/7 3/7

3/7 1/7 -1/7

2/35 3/35 4/35

 

Вопросы для самопроверки

1. Какие окна имеет интерфейс MATLAB и каково их назначение?

2. Какова структура командного окна Command Window?

3. Как называется отображение в командном окне сеанса работы с системой? На какие зоны подразделяется текстовое поле окна Command Window?

4. Для чего служат в MATLAB клавиши <↑> и <↓>?

5. Для чего применяется команда disp?

6. Как можно ввести слишком длинную команду в окне Command Window?

7. Какая информация сохраняется в окнах Command History и Workspase после применения команды очистки экрана clc?

8. Как получить справку по выбранной команде MATLAB?

9. В каких форматах представляются в MATLAB вещественные числа?

10. Какие форматы отображения вещественных чисел используются в MATLAB?

11. Как в в MATLAB осуществляются операции с комплексными числами?

12. В чем измеряются аргументы встроенных тригонометрических функций?

13. Какая команда осуществляет векторизацию символьного выражения?

14. Как MATLAB реагирует на ошибки ввода?

15. Как обнаружить и устранить семантическую ошибку ввода?

16. Как в MATLAB создаются векторы и матрицы?

17. Как осуществляется просмотр и редактирование переменных в окне Workspase?

18. Как в MATLAB осуществляются матричные и поэлементные операции над векторами и матрицами?

19. Что вычисляют команды dot и cross?

20. Как решается система линейных уравнений с помощью оператора обратного деления < \ >?

 

 

ГЛАВА 2 РАБОТА С МАССИВАМИ

Эта глава знакомит с другими способами создания векторов и матриц. В ней рассмотрены способы формирования массивов специального вида, создания новых массивов на основе существующих. Мы также ознакомимся с возможностями MATLAB для решения типовых задач линейной алгебры.

Создание векторов и матриц

 

Возможен ввод векторов в виде арифметических выражений, содержащих любые встроенные функции. Например:

>> V=[2+2/(3+4),exp(5),sqrt(10)]

V =

2.2857 148.4132 3.1623

Матрицы небольших размеров удобно вводить с командной строки следующим образом.. Вначале ставится открывающая квадратная скобка. Затем элементы каждой строки матрицы набираются через пробел или запятую, а ввод строки завершается нажатием на клавишу <Enter>. При вводе последней строки в конце ставится закрывающая квадратная скобка. Если после закрывающей квадратной скобки не ставить точку с запятой для подавления вывода в командное окно, то матрица выведется в виде таблицы. Пример:

>> B=[1 3 0

-2 -2 5]

B =

1 3 0

-2 -2 5

Еще один способ формирования векторных и матричных массивов в окне рабочего пространства Workspace рассмотрен в разделе 1.9.

Если в матрице

>> M=[1 2 3 4;5 6 7 8];

надо заменить элемент

>> disp(M(2,3))

некоторым числом, например π, то это можно сделать так:

>> M(2,3)=pi

M =

1.0000 2.0000 3.0000 4.0000

5.0000 6.0000 3.1416 8.0000

Обратите внимание на то, что если операция присваивания нового значения хотя бы одному элементу матрицы не завершена точкой с запятой, матрица М целиком выводится в командное окно.

Присвоить можно и значение элементу матрицы, индексы которого превышают текущие ее размеры. В этом случае эти размеры будут соответственно увеличены, а остальные элементы такой расширенной матрицы будут заполнены нулями:

>> A=[1 2]

A =

1 2

>> A(2,3)=5

A =

1 2 0

0 0 5

Длинный вектор можно вводить частями, которые затем объединяются с помощью операции сцепления строк:

>> V1=[1 2 3];V2=[4 5 6];

>> V=[V1 V2]

V =

1 2 3 4 5 6

Для создания нового вектора из определенных в заданном порядке элементов другого вектора применяется индексация при помощи вектора. Запись в вектор W пятого, второго, первого и третьего элементов вектора V производится следующим образом:

>> ind=[5 2 1 3];

>> W=V(ind)

W =

5 2 1 3

Пусть в векторе из девяти элементов требуется заменить нулями элементы с третьго по седьмой. Эту задачу легко решить индексацией с помощью двоеточия.

Например:

>> P=[-1 0.1 2.2 3.4 5.6 3.1 6.8 9.7 5.5];

>> P(3:7)=0

P =

-1.0000 0.1000 0 0 0 0 0 9.7000 5.5000

Указание номеров элементов вектора можно использовать и при вводе векторов, последовательно добавляя новые элементы (необязательно в порядке возрастания их номеров). Команды:

>> h=10;

>> h(2)=20;

>> h(4)=40;

приводят к образованию вектора:

>> h

h =

10 20 0 40

Заметим, что для ввода первого элемента h необязательно указывать его индекс, т. к. при выполнении оператора h=10 создается вектор (массив размера один на один). Следующие операторы присваивания приводят к автоматическому увеличению длины вектора h, а пропущенные элементы (в

нашем случае h(3)) получают значение ноль.

Массивы различаются по числу размерностей или измерений: одномерные, двумерные, многомерные. Размером массива называют число элементов вдоль каждого из измерений. Размер квадратной матрицы называется ее порядком.

Введем следующие массивы A, B, V, U, a:

>> A=[1,2;3,4],B=[1 2 3;4 5 6],V=[1 2 3],U=[1;2;3],a=5

A =

1 2

3 4

B =

1 2 3

4 5 6

V =

1 2 3

U =

a =

Команда size(A) выдает число строк и столбцов матрицы A:

>> disp(size(A))

2 2

>> disp(size(B))

2 3

>> disp(size(V))

1 3

>> disp(size(U))

3 1

>> disp(size(a))

1 1

Итак, A, B, V, U, a – массивы размеров 2×2, 2×3, 1×3, 3×1, 1×1 соответственно, причем A – квадратная матрица порядка 2.

Команда ndims(A) выдает размерность массива A:

>> disp(ndims(A))

>> disp(ndims(B))

>> disp(ndims(a))

>> disp(ndims(V))

Итак, A, B, a, V – массивы размерности 2 установленных ранее размеров.

Команда length(V) выдает число элементов вектора V, т. е. его длину:

>> disp(length(V))

В MATLAB можно создавать массивы размерности и выше 2.

Пример:

>> p(1,1,2)=1

p(:,:,1) =

p(:,:,2) =

>> disp(size(p))

1 1 2

>> disp(ndims(p))

Таким образом введен массив p размерности 3 размера 1×1×2 с двумя элементами p(1,1,1) = 0 и p(1,1,2) = 1.