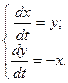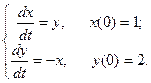Решение дифференциальных уравнений – команда dsolve

 

Для решения обыкновенных дифференциальных уравнений (систем уравнений) MATLAB имеет команду

r = dsolve('eq1','eq2',...,'cond1','cond2',...,'v').

Она возвращает аналитическое решение дифференциальных уравнений eq1, eq2,..., использующих v как независимую переменную, с граничными и (или) начальными условиями cond1, cond2,.... По умолчанию независимой переменной считается переменная t, обычно обозначающая время. Если в выражениях eqI (condI) не используется знак равенства, то полагается, что eqI (condI) = 0.

Символ D обозначает производную по независимой переменной, то есть d/dt, при этом D2 означает d²/dt² и т. д. Имя независимой переменной не должно начинаться с буквы D.

Начальные условия задаются в виде равенств 'y(a) = b' или 'Dy(a) = b', где у – зависимая переменная, a и b – константы, которые могут быть и символьными. Могут быть символьными и константы в уравнениях. Если число начальных условий меньше порядка уравнения, то в решении будут присутствовать произвольные постоянные C1, C2 и т. д. Формы вывода результата такие же, как и для команды solve. Справку по dsolve можно получить, введя команду doc dsolve.

Пример:

Решить дифференциальные уравнения

1) x'' = -2x', 2) y'' = -ax+y', y(0) = b, 3) y⁽⁴⁾ - y = 5e^xsinx+x⁴, 4) y''+4y'+3y = cost, y(0) = 1, y'(0) = 0.

Решения 3 - го и 4 - го уравнений проверить подстановкой.

Решение:

>> dsolve('D2x=-2*x')

ans =

C1*cos(2^(1/2)*t)+C2*sin(2^(1/2)*t)

>> dsolve('D2y=-a*x+y','y(0)=b','x')

ans =

a*x+C1*sinh(x)+b*cosh(x)

>> syms x

>> S=dsolve('D4y-y-5*exp(x)*sin(x)-x^4','x');

>> [R]=simple(S)

R =

-24-x^4-exp(x)*sin(x)+C1*exp(x)+C2*sin(x)+C3*cos(x)+C4*exp(-x)

Проверка 3 -го решения:

>> diff(R,x,4)-R-5*exp(x)*sin(x)-x^4

ans =

>> S=dsolve('D2y+4*Dy+3*y=cos(t)','y(0)=1','Dy(0)=0','t')

S =

1/10*cos(t)+1/5*sin(t)-7/20*exp(-3*t)+5/4*exp(-t)

Проверка 4 -го решения:

>> syms t

>> diff(S,t,2)+4*diff(S,t)+3*S

ans =

cos(t)

Проверка выполнения начальных условий 4 - го решения:

>> subs(S,t,0)

ans =

>> subs(diff(S,t),t,0)

ans =

Пример:

Решить систему линейных дифференциальных уравнений

 

 

Решение:

>> S=dsolve('Dx = y', 'Dy = -x')

S =

x: [1x1 sym]

y: [1x1 sym]

>> disp([S.x, S.y ])

[ cos(t)*C1+sin(t)*C2, -sin(t)*C1+cos(t)*C2]

Пример:

Решить систему линейных дифференциальных уравнений с начальными условиями и проверить решение

 

 

Решение:

>> S=dsolve('Dx = y', 'Dy = -x','x(0)=1','y(0)=2')

S =

x: [1x1 sym]

y: [1x1 sym]

>> disp([S.x S.y])

[ cos(t)+2*sin(t), -sin(t)+2*cos(t)]

Получено решение: x = cost+2sint, y = -sint+2cost.

Проверка решения:

syms t

>> diff(S.x,t)-S.y

ans =

>> diff(S.y,t)+S.x

ans =

Проверка выполнения начальных условий:

>> subs(S.x,t,0)

ans =

>> subs(S.y,t,0)

ans =

Команда dsolve не позволяет получить аналитическое решение дифференциального уравнения произвольного вида.

Пример:

Найти аналитическое решение уравнения Ван-дер-Поля

y'' - (1 - y²)y'+y = 0, y(0) = 2, y'(0) = 0.

Решение:

Обращение к dsolve выдает сообщение о том, что решение не найдено:

>> dsolve('D2y-(1-y^2)*Dy+y=0','y(0)=2','Dy(0)=0')

ans =

[ empty sym ]

В некоторых случаях dsolve возвращает решение, выраженное через специальные функции.

Пример:

Найти аналитическое решение уравнения Бесселя x²y''+xy'+(x² - v²)y = 0.

Решение:

>> dsolve('x^2*D2y+x*Dy+(x^2-v^2)*y=0','x')

ans =

C1*besselj(v,x)+C2*bessely(v,x)

Решение выражается через функции Бесселя. Информацию о функциях Бесселя можно получить с помощью команды doc besselj.

7.15 Прямое и обратное преобразования Лапласа – команды laplace, ilaplace

 

Преобразование Лапласа любой комплексной функции f(t) действительной переменной t имеет вид

L(s) = f(t)e^-stdt.

Функцию f(t) принятоназывть оригиналом, а функцию L(s) – изображением. Функция f(t) должна удовлетворять следующим условиям:

а) f(t) является непрерывной функцией для всех значений t, принадлежащих области определения. (Допускается наличие разрывов первого рода в конечном числе точек, расположенных на интервалах конечной длины. Количество таких интервалов должно быть конечным числом);

б) f(t) = 0 при t < 0;

в) существуют числа M > 0 и p ≥ 0 такие, что для всех t │ f(t) │ < Me^pt (p называется показателем роста │ f(t) │).

Некоторые простейшие) преобразования Лапласа приведены в таблице 7.1.

 

Таблица 7.1. Некоторые преобразования Лапласа

 

f(t)	L(s) = f(t)e^-stdt.
1	s^-1
e^-at	(s+a)^-1
sinat	a(s^2+a^2)^-1
t^n	n!s^-n-1
e^-atcoswt
t^ne^-at

 

В MATLAB преобразование Лапласа функции f(t) осуществляется с помощью команды laplace(F,t,s).

Найдем с помощью этой команды изображения заданных в таблице 7.1 оригиналов f(t):

>> syms a t w s

>> n=sym('n','positive');

>> laplace(1,t,s)

ans =

1/s

>> laplace(exp(-a*t),t,s)

ans =

1/(s+a)

>> laplace(sin(a*t),t,s)

ans =

a/(s^2+a^2)

>> laplace(t^n,t,s)

ans =

s^(-n-1)*gamma(n+1)

>> laplace(exp(-a*t)*cos(w*t),t,s)

ans =

(s+a)/((s+a)^2+w^2)

>> laplace(t^n*exp(-a*t),t,s)

ans =

gamma(n+1)*(s+a)^(-n-1)

Полученные изображения совпадают с табличными, если учесть, что

gamma(n+1) = n! для целых n (см. разд. 7.10).

Пример:

Найти изображение функции f(t) = e^-2tsin2tcos3t.

Решение:

>> syms t s

>> laplace(exp(-2*t)*sin(2*t)*cos(3*t),t,s)

ans =

5/2/((s+2)^2+25)-1/2/((s+2)^2+1)

>> pretty(ans)

1 1

5/2 ------------- - 1/2 ------------

2 2

(s + 2) + 25 (s + 2) + 1

>> factor(ans)

ans =

2*(s^2+4*s-1)/(s^2+4*s+29)/(s^2+4*s+5)

>> pretty(ans)

s + 4 s - 1

2 ------------------------------

2 2

(s + 4 s + 29) (s + 4 s + 5)

Итак,

L(s) = 2.

 

Пример:

Найти изображение функции f(t) =.

Решение:

При обращении к laplace команда возвращается без результата:

>> laplace(1/t,t,s)

ans =

laplace(1/t,t,s)

Это означает что либо изображения не существует, либо системе MATLAB не удалось его найти.

Существуют различные модификации laplace (справку можно получить с помощью команды doc laplace).

Обратное преобразование Лапласа имеет вид

 

f(t) = L(s)e^stds.

В среде MATLAB обратное преобразование Лапласа функции L(s) можно получить с помощью команды ilaplace(L,s,t). Найдем с ее помощью оригиналы заданных в таблице 7.1 изображений L(s):

>> syms a t w s

>> n=sym('n','positive');

>> ilaplace(1/s,s,t)

ans =

>> ilaplace(1/(s+a),s,t)

ans =

exp(-a*t)

>> ilaplace(a/(s^2+a^2),s,t)

ans =

a/(a^2)^(1/2)*sin((a^2)^(1/2)*t)

>> ilaplace(s^(-n-1)*gamma(n+1),s,t)

ans =

t^n

>> ilaplace((s+a)/((s+a)^2+w^2),s,t)

ans =

exp(-a*t)*cos(w*t)

>> ilaplace(gamma(n+1)*(s+a)^(-n-1),s,t)

ans =

exp(-a*t)*t^n

Полученные оригиналы совпадают с табличными.

Пример:

Найти оригинал полученного ранее изображения

 

2

функции f(t) = e^-2tsin2tcos3t.

Решение:

>> syms t s

>> ilaplace(2*(s^2+4*s-1)/(s^2+4*s+29)/(s^2+4*s+5),s,t)

ans =

1/2*exp(-2*t)*sin(5*t)-1/2*exp(-2*t)*sin(t)

>> factor(ans)

ans =

1/2*exp(-2*t)*(sin(5*t)-sin(t))

Поскольку (sin5t - sint) = sin2tcos3t, то оригинал найден верно.

Пример:

Найти оригинал изображения

L(s) =.

 

Решение:

Команда ilaplace возвращает решение, выраженное через функцию Хевисайда:

>> syms t s a

>> ilaplace(exp(-2*s)/(s+a),s,t)

ans =

Heaviside(t-2)*exp(-a*(t-2))

Функция Хевисайда (единичная функция) определяется следующим образом:

 

δ₀(t) =

 

Следовательно, найденный оригинал имеет вид

 

f(t) =

 

Пример:

Найти оригинал изображения

L(s) =.

 

Решение:

Команда ilaplace возвращает решение, выраженное через корни уравнения z⁴+1 = 0:

>> syms t s

>> ilaplace((s^4-1)/(s^5+s),s,t)

ans =

-1+2*sum(1/4*exp(_alpha*t),_alpha = RootOf(_Z^4+1))

Команда vpa вычисляет приближенное значение оригинала с заданным количеством текущих цифр:

>> vpa(ans,4)

ans =

-1.+1.000*exp(-.7071*t)*cos(.7071*t)+1.000*exp(.7071*t)*cos(.7071*t)

Пример:

Найти оригинал изображения

L(s) =.

 

Решение:

Команда ilaplace возвращается без результата:

>> syms t s

>> ilaplace(exp(2*s)/(s+3)^2,s,t)

ans =

ilaplace(exp(2*s)/(s+3)^2,s,t)

Это означает что либо оригинала не существует, либо системе MATLAB не удалось его найти.

Существуют и другие модификации ilaplace (справку можно получить, введя команду doc ilaplace).