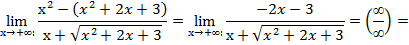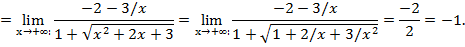Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функции одной переменной и их пределыСодержание книги
Поиск на нашем сайте
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И КОНТРОЛЬНЫЕ ЗАДАНИЯ ПО ДИСЦИПЛИНЕ «МАТЕМАТИКА» ДЛЯ СТУДЕНТОВ ЗАОЧНОГО ОБУЧЕНИЯ Воркута Рассмотрено и рекомендовано циклом общих математических и естественно научных дисциплин. Введение. В настоящих методических указаниях, предназначенных для студентов заочного факультета, кратко излагаются основы теоретические положения курса Математики. Рассматриваются типовые задачи и приводятся их решение с объяснением. Методические материалы предназначены для оказания помощи студенты при самостоятельном изучении материала и выполнении контрольных работ по темам, входящим в программу 1 части курса математики. Методические указания содержат 10 вариантов контрольной работы, которую студент должен выполнить, согласно программе.
Составитель: преподаватель математики И.А.Калинкина
Рецензенты: зам. директора по НМР А.В.Корда зам директора по УР М.М. Ткачук Программа Тема 1: Предел и непрерывность функции. Тема 2: Производная. Дифференциал функции и его приложения. Тема 3: Приложения производной к исследованию функции и построению графиков. Тема 4: Неопределенные интегралы. Тема 5: Определенный интеграл и его приложения. Тема 6: Комплексные числа. Тема 7: Дифференциальные уравнения. Тема 8: Элементы теории вероятностей и математической статистики. Экзаменационные вопросы. 1. Функция, числовая функция, способы задания. Область определения и область изменения функции. Основные свойства (монотонность, четность, периодичность). 2. Числовая последовательность, способы задания и способы изображения числовой последовательности. Свойства числовой последовательности. 3. Предел числовой последовательности и его геометрический смысл. 4. Теоремы о пределах числовой последовательности. 5. Бесконечно малые и бесконечно большие последовательности. 6. Правило раскрытия неопределенности вида 7. Предел функции в точке и его геометрический смысл. 8. Правило раскрытия неопределенности вида 9. Определение производной, её физический и геометрический смысл. 10. Формулы дифференцирования. 11. Дифференциал функции и его геометрический смысл. 12. Вторая производная я и ее физический смысл.
13. Сложная функция и правило ее дифференцирования. 14. Монотонность функции, признак монотонности. 15. Исследование функции на наименьшее и наибольшее значение в некотором промежутке. 16. Выпуклость графика функции, признак выпуклости. 17. Точки перегиба, признак точек перегиба. 18. Алгоритм исследования функции с помощью производной. 19. Понятие первообразной функции. 20. Неопределенный интеграл, компоненты, свойства. 21. Таблица неопределенных интегралов, их доказательство. 22. Способы интегрирования. 23. Определенный интеграл, компоненты, свойства. 24. Формулы Ньютона-Лейбница. 25. Вычисление площадей плоских фигур с помощью интеграла. 26. Решение физических задач с помощью интеграла. 27. Дифференциальные уравнения. 28. Геометрические приложения неопределенного интеграла. Введение в анализ Производная Производной функцией f(x) в точке
Функции f(x), имеющая производную в каждой точке некоторого промежутка, называется дифференцируемой в этом промежутке. Основные правила дифференцирования. Производная алгебраической суммы функций
Производная произведения двух функций
Производная произведения трех функций
Производная произведения постоянной на функцию
Производная частного (дроби)
Частные случаи формулы (5):
При условии u=x C'=0, (8)
x'=1, (9)
При условии
ПРИМЕРЫ: 1) Найти производную следующей функции:
Решение: 2) Используем формулы (2), (1), (10а), (8), (9), находим Решение: 3) Используем формулы (5), (1), (10а), (8), получим Решение: 4) Решение: По формуле производной произведения получим:
Найдем производные в каждом из слагаемых и выполним преобразования:
Точки перегиба Точка графика функции y=f(x), разделяющая промежутки выпуклости противоположных направлений этого графика, называется точкой перегиба. Правило нахождения точек перегиба графика функции y=f(x) I. Найти вторую производную
II. Найти критические точки функции y=f(x), в которых III. Исследовать знак второй производной которые найденные критические точки делят область определения функции f(x). Если при этом критическая точка IV. Вычислить значения функции в точках перегиба. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ Интегрируя обе части равенства d(uv)=udv+vdu, получим ∫ d(uv)= ∫ udv +∫ vdu; uv= ∫ udv+ ∫ vdu, Откуда ∫udv=uv-∫vdu С помощью этой формулы вычисление интеграла ∫ udv сводится к вычислению интеграла∫ vdu, если последний окажется проще исходного. Пример: найти следующие интегралы: 1) 1) Положим u=x, dv=sinxdx; тогда du=dx, ∫dv=∫sinxdx, т.е. v=-cosx. Используя формулу (11.14), получим
2) Положим u =ln x,
3) Положим По формуле (11.14) получим
В числителе подынтегральной функции последнего интеграла прибавим и вычтем а 2 и представим этот интеграл в виде суммы двух интегралов:
Последний интеграл находим по формуле (11.11):
Перенеся
Или окончательно
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ КОМПЛЕКСНЫЕ ЧИСЛА Комплексными числами называют числа вида a+bi, где aи b– действительные числа, а число i, определяемое равенством 1) Два комплексных числа 2) Суммой двух комплексных чисел 3) Произведением двух комплексных чисел
ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ, ЗАДАННЫМИ В АЛГЕБРАИЧЕСКОЙ ФОРМЕ. Над комплексными числами производится такие же действия, как и над действительными числами. Действия сложения и умножения даны в определении комплексного числа. Рассматривая вычитание и деление комплексных чисел как действия, обратные соответственно сложению и умножению, получаем правила вычитания и деления комплексных чисел:
Выполнить действия: 1) (4+2i)+(1+5i); 2) (3 + 5i) – (6 + 3i). 1) По правилу сложения комплексных чисел получим (4 + 2i) + (1 + 5i) = (4 + 1) + (2 + 5)i = 5 + 7i. 2) По правилу вычитания комплексных чисел получим (3 + 5i) – (6 + 3i) = (3 - 6) + (5 - 3)i = - 3 + 2i.
Сложение (вычитание) комплексных чисел сводится к сложению (вычитанию) векторов, изображающих эти числа. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ Характер частного решения z неоднородного уравнения у" + ру' + qу = f(х) (р и q постоянны) в зависимости от правой части f(х)
Контрольные задания Задание 1: Вычислить пределы
Задание 2: Найти производные указанных функций
Задание 3: Найти точки экстремума функции
Задание 4: Исследовать функцию с помощью производной и построить график
Задание 5: Найти интеграл
Задание 6: Вычислить определённые интегралы
Задание 7: Вычислить площади фигур, ограниченных линиями.
Задание 8: Решить дифференциальные уравнения
ПРАВИЛА ВЫПОЛНЕНИЯ И ОФОРМЛЕНИЯ КОНТРОЛЬНЫХ РАБОТ. При выполнении контрольных работ необходимо придерживаться ниже изложенных правил. Работы, выполненные без соблюдения этих правил, не зачитываются и возвращаются студенту для переработки. 1. Контрольную работу следует выполнять в тетради, отдельной для каждой работы, чернилами любого цвета, кроме красного, оставляя поля для замечаний рецензента.
2. На обложке тетради должны быть ясно написаны фамилия студента, его инициалы, учебный номер (шифр), номер контрольной работы, название дисциплины; В конце работы следует проставить дату её выполнения и расписаться.
3. В работу должны быть включены все задачи, указанные в задания, строго по своему варианту. Контрольные работы, содержащие не все задания, а также содержащие задачи другого варианта, не засчитываются.
4. Решения задач надо располагать в порядке возрастания номеров, сохраняя номера задач.
5. После выполнения всех заданий, указать список литературы, которую использовали при решении.
6. Перед решением каждой задачи надо выписать полностью её условие, подставляя конкретные данные из решаемого варианта.
7. Решение задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи. 8. После получения прорецензированной работы, как зачтенной, так и не зачтенной, студент должен исправить все указанные рецензентом ошибки и недочеты и выполнить все рекомендации рецензента. Исправления следует присылать вместе с прорецензированной работой и рецензией. В связи с этим рекомендуется оставлять в конце тетради несколько чистых листов для дополнений и исправлений в соответствии с указаниями рецензента. Вносить исправления в сам текст работы после её рецензирования запрещается. В случае незачета работы и отсутствия прямого указания на то, что студент может ограничиться исправлением отдельных задач, вся работа должна быть выполнена заново.
9. Поскольку на рецензирование работы преподавателю отводится две недели, задания следует сдавать на проверку заблаговременно.
10. К экзамену допускаются студенты, получившие положительную рецензию на работу.
Основные источники: 1. Богомолов, Н.В., Сергиенко, Л.Ю. Математика. Дидактическое издание. Издательство «Дрофа» 2010. 2. Григорьева, С.Г., Задулина, С.В. Математика Издательство ОИЦ«Академия» 2010. Интернет-ресурсы: http://siblec.ru - Справочник по высшей математике; http://matclub.ru - В ысшая математика, лекции.примеры решения задач, ТФКП, электронные учебники Дополнительные источники: • Григорьев, С.В., Гусев, В.А., Иволгина С.В. Математика для профессий и специальностей социально-экономического профиля. Издательство ОИЦ «Академия» 2010. • Пехлицкий,И.Д. Математика Издательство ОИЦ «Академия» 2010. МЕТОДИЧЕСКИЕ УКАЗАНИЯ И КОНТРОЛЬНЫЕ ЗАДАНИЯ ПО ДИСЦИПЛИНЕ «МАТЕМАТИКА» ДЛЯ СТУДЕНТОВ ЗАОЧНОГО ОБУЧЕНИЯ Воркута Рассмотрено и рекомендовано циклом общих математических и естественно научных дисциплин. Введение. В настоящих методических указаниях, предназначенных для студентов заочного факультета, кратко излагаются основы теоретические положения курса Математики. Рассматриваются типовые задачи и приводятся их решение с объяснением. Методические материалы предназначены для оказания помощи студенты при самостоятельном изучении материала и выполнении контрольных работ по темам, входящим в программу 1 части курса математики. Методические указания содержат 10 вариантов контрольной работы, которую студент должен выполнить, согласно программе.
Составитель: преподаватель математики И.А.Калинкина
Рецензенты: зам. директора по НМР А.В.Корда зам директора по УР М.М. Ткачук Программа Тема 1: Предел и непрерывность функции. Тема 2: Производная. Дифференциал функции и его приложения. Тема 3: Приложения производной к исследованию функции и построению графиков. Тема 4: Неопределенные интегралы. Тема 5: Определенный интеграл и его приложения. Тема 6: Комплексные числа. Тема 7: Дифференциальные уравнения. Тема 8: Элементы теории вероятностей и математической статистики. Экзаменационные вопросы. 1. Функция, числовая функция, способы задания. Область определения и область изменения функции. Основные свойства (монотонность, четность, периодичность). 2. Числовая последовательность, способы задания и способы изображения числовой последовательности. Свойства числовой последовательности. 3. Предел числовой последовательности и его геометрический смысл. 4. Теоремы о пределах числовой последовательности. 5. Бесконечно малые и бесконечно большие последовательности. 6. Правило раскрытия неопределенности вида 7. Предел функции в точке и его геометрический смысл. 8. Правило раскрытия неопределенности вида 9. Определение производной, её физический и геометрический смысл. 10. Формулы дифференцирования. 11. Дифференциал функции и его геометрический смысл. 12. Вторая производная я и ее физический смысл. 13. Сложная функция и правило ее дифференцирования. 14. Монотонность функции, признак монотонности. 15. Исследование функции на наименьшее и наибольшее значение в некотором промежутке.
16. Выпуклость графика функции, признак выпуклости. 17. Точки перегиба, признак точек перегиба. 18. Алгоритм исследования функции с помощью производной. 19. Понятие первообразной функции. 20. Неопределенный интеграл, компоненты, свойства. 21. Таблица неопределенных интегралов, их доказательство. 22. Способы интегрирования. 23. Определенный интеграл, компоненты, свойства. 24. Формулы Ньютона-Лейбница. 25. Вычисление площадей плоских фигур с помощью интеграла. 26. Решение физических задач с помощью интеграла. 27. Дифференциальные уравнения. 28. Геометрические приложения неопределенного интеграла. Введение в анализ Функции одной переменной и их пределы Для успешного задания из настоящего раздела необходимо изучать теоретический материал, обратив особое внимание на понятия функции, ее области определения, бесконечно малой и бесконечно большой величин, предела и непрерывности функции; овладев основными приемами вычисления пределов неопределенных выражений (неопределенностей) различный типов с использованием классических пределов и эквивалентных малых. Для раскрытия неопределенности типа (∞/∞) используют деления числителя и знаменателя на самое быстро растущее слагаемое, например, на старшую степень x при x→∞:
Неопределенность типа (∞-∞) предварительно следует привести к типу (∞/∞). Например,
Для раскрытия неопределенности типа (0/0) возникающей при причине предела рациональной дроби (отношения многочленов), многочлены в числителе и знаменателе разлагают на множители:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 404; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.149.14 (0.013 с.) |



 называется предел отношения приращения
называется предел отношения приращения  функции в этой точке к приращению
функции в этой точке к приращению  аргумента, когда последнее стремится к нулю:
аргумента, когда последнее стремится к нулю: .
.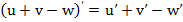 . (1)
. (1)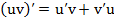 . (2)
. (2) . (3)
. (3)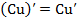 . (4)
. (4)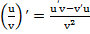 . (5)
. (5) ; (6)
; (6) . (7)
. (7)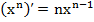 , где n-любое действительное число, (10а)
, где n-любое действительное число, (10а)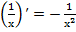 , (11a)
, (11a)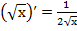 , (12a)
, (12a)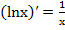 , (13a)
, (13a) , (14a)
, (14a) , (15a)
, (15a)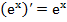 , (16a)
, (16a)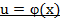
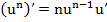 , где n-любое действительное число, (10)
, где n-любое действительное число, (10) , (11)
, (11) , (12)
, (12)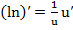 , (13)
, (13)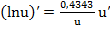 , (14)
, (14)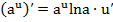 , (15)
, (15)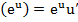 , (16)
, (16)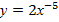
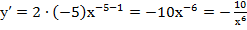
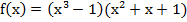


 .
.
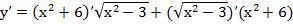 .
. .
.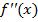 .
.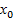 разделяет промежутки выпуклости противоположных направлений, то
разделяет промежутки выпуклости противоположных направлений, то  2)
2) 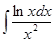 ; 3)
; 3) 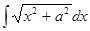 .
.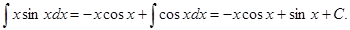
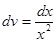 ; тогда
; тогда 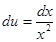 ,
, 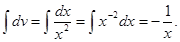 По формуле (11.14) получим
По формуле (11.14) получим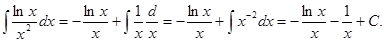
 тогда
тогда 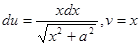 .
.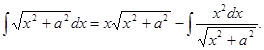
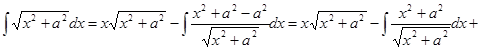


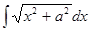 из правой части в левую, получим
из правой части в левую, получим
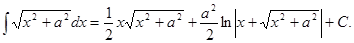
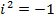 , называется мнимой единицей, если для этих чисел понятия равенства и действия сложения и умножения определены следующим образом:
, называется мнимой единицей, если для этих чисел понятия равенства и действия сложения и умножения определены следующим образом: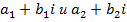 называются равными, если
называются равными, если 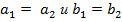 ;
; ;
;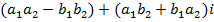 .
.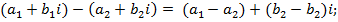
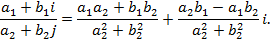


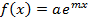 (a, m постоянные)
(a, m постоянные)
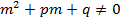 ,
2.
,
2.  .
a)
.
a) 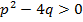 ,
b)
,
b)  .
.
 ,
z=A
,
z=A 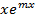 ,
z=A
,
z=A  .
.
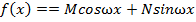 (M, N,
(M, N,  постоянны)
постоянны)
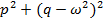 ≠0,
2.
≠0,
2. 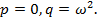
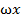 +
Bsin
+
Bsin 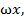 z=x(Acos
z=x(Acos  (a, b, c постоянны)
(a, b, c постоянны)
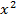 +Bx+C,
z= x(A
+Bx+C,
z= x(A 
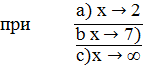
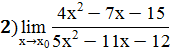

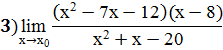
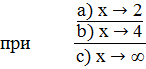



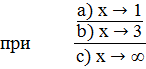
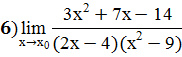
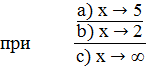

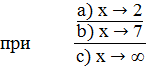
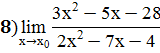
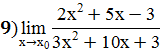
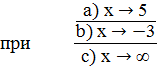


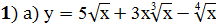
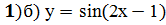

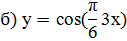
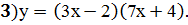
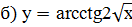
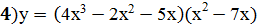

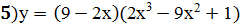
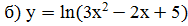

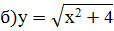
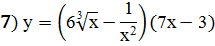
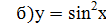

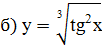
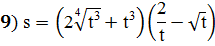
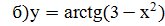
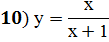
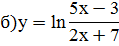
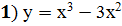
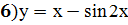
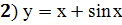
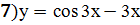
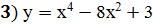

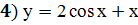
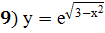
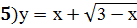

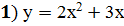
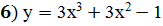



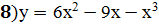
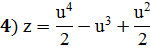
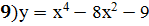
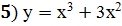
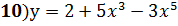
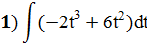
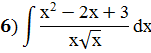
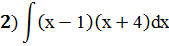
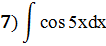
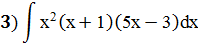
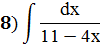

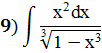
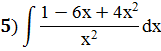
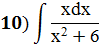

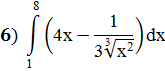
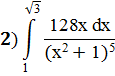



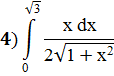

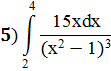
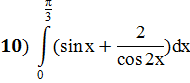
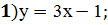


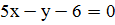

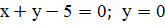
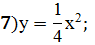
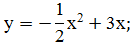
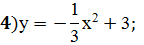
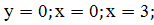
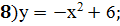
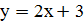

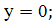

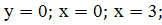

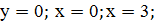

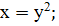

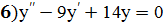
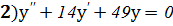

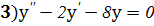
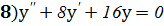
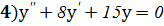

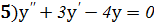

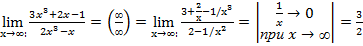 ;
;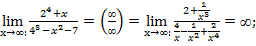
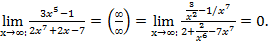
 (x-
(x- 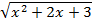 )=(∞-∞)=
)=(∞-∞)= 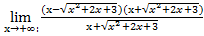 =
=