
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приложения производной к исследованию функций.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Функция y=f(x) называется возрастающей в промежутке a<x<b, если для любых Функция y=f(x) называется убывающей в промежутке u<x<b, если для любых Как возрастающие, так и убывающие функции называются монотонными, а промежутки, в которых функция возрастает или убывает, - промежутками монотонности. Возрастание и убывание функции y=f(x) характеризуется знаком ее производной: если в некотором промежутке Правило нахождения экстремумов функции y=f(x) с помощью первой производной. Найти производную f '(x). Найти критические точки функции y=f(x), т.е. точки, в которых f '(x) обращается в нуль или терпит разрыв. Исследовать знак производной f '(x) в промежутках, на которые найденные критические точки делят область определения функции f(x). При этом критическая точка Вычислить значения функции в точках экстремума. Исследовать на экстремум следующие функции: ПРИМЕР:
Решение: Находим
График функции парабола, изображенная на рисунке. Точка минимум (2;-4) является вершиной параболы. Правила нахождения экстремумов функции y=f(x) с помощью второй производной. Найти производную f '(x). Найти критические точки данной функции, в которых f '(x)=0. Найти вторую производную f ''(x). Исследовать знак второй производной в каждой из критических точек. Если при этом вторая производная окажется отрицательной, то функция в такой точке имеет максимум, а если положительный, то – минимум. Если же вторая производная ровна нулю, то экстремум функции надо искать с помощью первой производной. Вычислить значения функции в точках экстремума. ПРИМЕР: Исследовать на экстремум с помощью второй производной функции:
Решение: 1) Находим производную: теперь вторую производную: 2) Находим
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 756; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.70.210 (0.006 с.) |

 ,принадлежащих этому промежутку и таких, что
,принадлежащих этому промежутку и таких, что  , имеет место неравенство
, имеет место неравенство 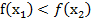 .
. .
. , то функция возрастает в этом промежутке; если же
, то функция возрастает в этом промежутке; если же  , то функция убывает в этом промежутке.
, то функция убывает в этом промежутке.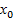 есть точка минимума, если она отделяет промежуток, в котором f '(x) < 0, от промежутка, в котором f '(x) > 0, и точка максимума – в противном случае. Если же в соседних промежутках, разделенной критической точкой
есть точка минимума, если она отделяет промежуток, в котором f '(x) < 0, от промежутка, в котором f '(x) > 0, и точка максимума – в противном случае. Если же в соседних промежутках, разделенной критической точкой 
 . Полагая
. Полагая  , получим единственную критическую точку ч=2. Дальнейшие рассуждения представлены в таблице:
, получим единственную критическую точку ч=2. Дальнейшие рассуждения представлены в таблице:
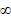




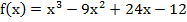 .
. . Решая уравнение
. Решая уравнение  , получим критическую точку х=1. Найдем
, получим критическую точку х=1. Найдем . Так как вторая производная в критической точке положительна, то при х=1 функция имеет минимум:
. Так как вторая производная в критической точке положительна, то при х=1 функция имеет минимум: 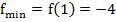 .
. . Найдем теперь
. Найдем теперь  . Определим знак второй производной в критических точках. Так как
. Определим знак второй производной в критических точках. Так как  , то при х=2 функция имеет максимум; так как
, то при х=2 функция имеет максимум; так как  , то при х=4 функция имеет минимум. Вычислим значения функции в точках экстремума:
, то при х=4 функция имеет минимум. Вычислим значения функции в точках экстремума:  .
.


