Численное вычисление производной функции одного переменного

Известно, что численными приближенными методами производная функции в заданной точке может быть вычислена с использованием формулы конечных разностей. Выражение для вычисления производной функции одной переменной в точке х_k записанное в конечных разностях, имеет вид

,

где Δх – очень малая конечная величина.

При достаточно малых значениях Δх, можно с приемлемой точностью получить величину производной функции в точке. Для вычисления производной в MS Excel будем использовать приведенную выше формулу. Рассмотрим технологию вычисления производной на примере.

Пример 1.18 Найти производную функции у = 2х³ + х² в точке х=3. Заметим, что производная приведенной функции в точке х=3, вычисленная аналитическим методом, равна 60 - это значение нам понадобится для проверки результата, полученного путем вычисления численным методом.

Задачу вычисления производной в табличном процессоре можно решать двумя способами.

Решение первым способом

Введем в ячейку рабочего листа формулу правой части заданной функциональной зависимости например в ячейку В2, как показано на рисунке, делая ссылку на ячейку, где будет находиться значение х, например А2,

=2*А2^{^}3+А2^{^}2.

Зададим окрестность точки х=3 достаточно малого размера, например значение слева х_k=2,9999999, а значение справа х_k+1=3,00000001, и введем эти значения в ячейку А2 и А3 соответственно. В ячейку С2 введем формулу вычисления производной =(В3-В2)/(А3-А2).

В результате вычисления в ячейку С2 будет выведено приближенное значение производной заданной функции в точке х=3, величина которой равна 60, что соответствует результату, полученному аналитически (рис.1.24).

Рис. 1.24

Решение вторым способом

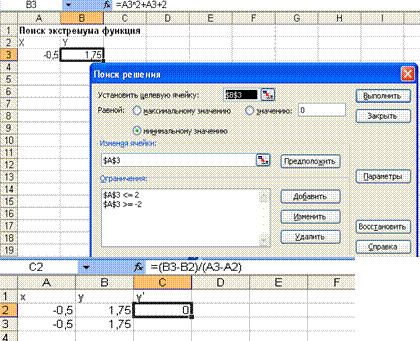
Введем в ячейку рабочего листа А2 заданное значение аргумента, равное 3, в ячейке В2 укажем достаточно малое приращение аргумента - (1E - 9), в ячейку С2 введем формулу для вычисления производной

=(2*(А2+В2)^{^}3+(А2+В2)^{^}2-(2*А2^{^}3+А2^{^}2))/В2.

После нажатия клавиши <Enter> получим результат вычисления 60,0000.

Как видим, результат получен такой же, как и при первом способе. Приведенный второй способ является более предпочтительным в случаях, когда нужно построить таблицу значений производной функции для заданных значений аргумента.

Вычисление локальных экстремумов функции

Напомним, что функция Y=f(x) имеет экстремум при значении х = х_k если производная функции в этой точке равна нулю.

Если функция f(x) непрерывна на отрезке [а, b] и имеет внутри этого отрезка локальный экстремум, то его можно найти, используя надстройку Excel Поиск решения.

Рассмотрим последовательность нахождения экстремума функции на примере

Пример 1.19 Задана неразрывная функция у = х² + х + 2. Требуется найти ее экстремум (минимальное значение) на отрезке [-2; 2].

Решение

В ячейку A3 рабочего листа введем любое число, принадлежащее заданному отрезку, в этой ячейке будет находиться значение х.

В ячейку В3 введем формулу, определяющую заданную функциональную зависимость. Вместо переменной х в этой формуле должна быть ссылка на ячейку А3: =А3^2+A3+2.

Выполним команду меню Сервис/Поиск решения.

В открывшемся окне диалога Поиск решения в поле Установить целевую ячейку укажем адрес ячейки, содержащей формулу (В3), установим переключатель Минимальному значению, в поле Измени ячейки укажем адрес ячейки, в которой содержится переменная х-A3.

Добавим два ограничения в соответствующее поле: A3 > = - 2 и A3<=2 (рис. 1.25).

 

 

 

Рис. 1.25

 

Щелкнем на кнопке Параметры и в открывшемся диалоговом окне параметры поиска решения установим относительную погрешность вычислений и предельное число итераций.

Щелкнем на кнопке Выполнить. В ячейке А3 будет вычислено значение аргумента х функции, при котором она принимает минимальное значение, а в ячейке В3 – минимальное значение функции.

В результате выполнения вычислений в ячейке А3 будет получено значение независимой переменной, при котором функция принимает наименьшее значение -0,5, а в ячейке В3 – минимальное значение, равное 1,75.

Построим график заданной функции и убедимся, что решение уравнения найдено, верно.

Примечание. В частном случае при нахождении локального экстремума с использованием рассмотренной технологии, можно получить значение, которое не является экстремумом, а просто является минимумом или максимумом функции в заданном диапазоне изменения аргумента.

Поэтому необходима дополнительная проверка, т.е. вычисление производной функции в найденной точке.

Используя приведенную технологию численного вычисления производной функции в заданной точке, проверим, является ли найденная точка х = -0,5 точкой экстремума функции у = х² + х + 2. Решение приведено на рисунке.

Как видно, производная в найденной точке равна нулю, следовательно, найденное значение функции является ее экстремальным значением.

Пример 1.20 Требуется найти значения аргумента в диапазоне [-1; 1], при которых функция у = х² + х + 2 имеет экстремумы.

Решение

Табулируем заданную функцию с шагом 0,2.

Применяя второй из приведенных способов вычисления производной, вычислим значения функции у = f(x + dx).

Вычислим значения производной при каждом табличном значении аргумента.

Анализируя полученные значения производных функции в точках, находим, что производная меняет знак в интервале значений аргумента (-0,6;-0,4), следовательно, на этом интервале есть точка экстремума. Кроме того, заметим, что знак производной меняется с минуса на плюс, следовательно, точка экстремума является минимумом функции.

Применяя инструмент Подбор параметра или Поиск решения для решения уравнения Y(x) = 0

 

Рис. 1.26

 

относительно х, вычислим точное значение аргумента, при котором исходная функция принимает экстре малыше значение (-0,5) (рис. 1.26).

Полученное значение производной исследуемой функции в точке х =-0,5 равно нулю, следовательно, в этой точке функция имеет экстремум.