

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Раздел VII. Функции нескольких переменных
Оглавление
Раздел VII. Функции нескольких переменных. 4
Основные понятия. 4
Частные производные. 18
Частные производные высших порядков. 25
Производная по направлению и градиент. 29
Экстремумы функций двух переменных. 41
Раздел VIII. Неопределенный интеграл. 55
Основные понятия. 55
Таблица (простая) интегралов. 57
Свойства неопределенного интеграла. 59
Внесение под знак дифференциала и обобщенная таблица интегралов. 65
Замена переменной в неопределенном интеграле. 68
Интегрирование по частям.. 73
Интегрирование выражений, содержащих логарифмы.. 78
Интегрирование выражений, содержащих тригонометрические функции. 80
Интегрирование рациональных функций. 85
Интегрирование некоторых иррациональных выражений. 91
Раздел VII. Функции нескольких переменных
Основные понятия
Ранее рассматривали функции, которые выражали зависимость некоторого фактора (переменной) от одного другого фактора (переменной). Записывали в виде  . Многие реальные зависимости в действительности таковыми и являются. Например: . Многие реальные зависимости в действительности таковыми и являются. Например:  − площадь круга, зависит только от значения одной переменной − площадь круга, зависит только от значения одной переменной 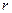 − радиуса круга; − радиуса круга;  − площадь квадрата, зависит только от одной переменной − площадь квадрата, зависит только от одной переменной 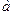 − длины стороны квадрата; − длины стороны квадрата;  − зависимость пройденного пути от времени (при заданной постоянной скорости − зависимость пройденного пути от времени (при заданной постоянной скорости 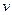 ) − функция только от времени движения ) − функция только от времени движения 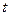 ; ;  − зависимость прибыли − зависимость прибыли  некоторого производства от вложенных в него средств некоторого производства от вложенных в него средств  ; ;  − зависимость объема урожая − зависимость объема урожая 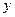 от количества внесенных удобрений от количества внесенных удобрений  − и так далее. Но в реальности чаще исследуемый фактор зависит не от одного, а от многих других факторов. Площадь прямоугольника − и так далее. Но в реальности чаще исследуемый фактор зависит не от одного, а от многих других факторов. Площадь прямоугольника  , ,  − зависимость пройденного пути от времени и скорости (т.е. от 2-х переменных − скорости и времени движения), − зависимость пройденного пути от времени и скорости (т.е. от 2-х переменных − скорости и времени движения),  − объем параллелепипеда (от 3-х – длин ребер). Более точная зависимость прибыли − объем параллелепипеда (от 3-х – длин ребер). Более точная зависимость прибыли  от вложенных в производство средств от вложенных в производство средств  будет получаться, если ввести отдельные переменные: будет получаться, если ввести отдельные переменные:  (капитал) – средства, вложенные в материалы, оборудование и (капитал) – средства, вложенные в материалы, оборудование и  (труд) – средства, вложенные в трудовые ресурсы; тогда (труд) – средства, вложенные в трудовые ресурсы; тогда  . Более точная зависимость урожайности от количества удобрений дифференцирует (в смысле «различает») количество вложенных удобрений разного типа (например, фосфорные и калийные): . Более точная зависимость урожайности от количества удобрений дифференцирует (в смысле «различает») количество вложенных удобрений разного типа (например, фосфорные и калийные): 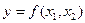 . Поэтому переходим к изучению функций многих переменных. Перенесем известные понятия, проходимые для функций одного переменного, на функции многих переменных (в основном, на примере функций двух и трех переменных). Общая форма записи функций двух и трех переменных: . Поэтому переходим к изучению функций многих переменных. Перенесем известные понятия, проходимые для функций одного переменного, на функции многих переменных (в основном, на примере функций двух и трех переменных). Общая форма записи функций двух и трех переменных:  и и  – по аналогии с функцией одного переменного – по аналогии с функцией одного переменного  (конечно, буквы, обозначающие переменные, могут быть и другими). Сначала дадим определение функции двух переменных, аналогичное даваемому ранее определению функции одного переменного. (конечно, буквы, обозначающие переменные, могут быть и другими). Сначала дадим определение функции двух переменных, аналогичное даваемому ранее определению функции одного переменного.
Переменная  называется функцией переменных называется функцией переменных  и и 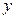 , если имеется правило, по которому каждой (допустимой!) паре числовых значений переменных , если имеется правило, по которому каждой (допустимой!) паре числовых значений переменных  ставится в соответствие некоторое (одно) числовое значение переменной ставится в соответствие некоторое (одно) числовое значение переменной  . Точно так же, переменная . Точно так же, переменная  называется функцией трех переменных называется функцией трех переменных  , , 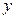 и и  , если имеется правило, по которому каждой допустимой тройке числовых значений переменных , если имеется правило, по которому каждой допустимой тройке числовых значений переменных  ставится в соответствие некоторое (одно) числовое значение переменной ставится в соответствие некоторое (одно) числовое значение переменной  . Аналогично определяется и функция любого числа переменных. . Аналогично определяется и функция любого числа переменных.
 Для функции одного переменного Для функции одного переменного  числовое значение аргумента числовое значение аргумента  геометрически изображали точкой на числовой оси геометрически изображали точкой на числовой оси  . Появлялось понятие области определения функции . Появлялось понятие области определения функции  как некое подмножество числовой прямой, точки которого (а это и точки и числа) можно подставлять в формулу, задающую функцию. Например, областью определения функции как некое подмножество числовой прямой, точки которого (а это и точки и числа) можно подставлять в формулу, задающую функцию. Например, областью определения функции  является следующее подмножество числовой прямой: является следующее подмножество числовой прямой:  . Таким образом, область определения функции одного переменного – некоторое подмножество точек (числовой) прямой. Для функции же двух переменных . Таким образом, область определения функции одного переменного – некоторое подмножество точек (числовой) прямой. Для функции же двух переменных  аргументом является пара чисел аргументом является пара чисел  . Попробуем аналогично все пары чисел тоже геометрически изобразить точками. Чтобы изобразить точкой пару чисел, придется от числовой прямой х перейти к координатной плоскости . Попробуем аналогично все пары чисел тоже геометрически изобразить точками. Чтобы изобразить точкой пару чисел, придется от числовой прямой х перейти к координатной плоскости 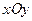 . Действительно, каждая пара чисел . Действительно, каждая пара чисел  может быть изображена точкой может быть изображена точкой  на координатной плоскости на координатной плоскости 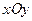 , для которой эта пара чисел является ее координатами (см. рисунок). , для которой эта пара чисел является ее координатами (см. рисунок).
Функцию двух переменных  тоже в общем случае можно вычислить не для любой пары чисел тоже в общем случае можно вычислить не для любой пары чисел  (другими словами, не в любой точке координатной плоскости (другими словами, не в любой точке координатной плоскости 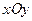 ). Например, если ). Например, если  , то эту функцию нельзя вычислить при , то эту функцию нельзя вычислить при  (другими словами, в точке (другими словами, в точке  ), поскольку в этом случае под логарифмом получается отрицательное число. Если собрать все пары чисел ), поскольку в этом случае под логарифмом получается отрицательное число. Если собрать все пары чисел  , которые можно подставлять в формулу , которые можно подставлять в формулу  для функции, и изобразить их соответствующими точками на координатной плоскости, то эти точки будут образовывать фигуру, которая называется областью определения функции для функции, и изобразить их соответствующими точками на координатной плоскости, то эти точки будут образовывать фигуру, которая называется областью определения функции  . Итак, областью определения функции двух переменных . Итак, областью определения функции двух переменных  называется фигура на координатной плоскости называется фигура на координатной плоскости 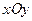 , состоящая из точек, координаты которых можно подставлять в формулу , состоящая из точек, координаты которых можно подставлять в формулу  , которой задается функция. Область определения может представлять собой фигуру любой формы. Более того, для любой фигуры на плоскости , которой задается функция. Область определения может представлять собой фигуру любой формы. Более того, для любой фигуры на плоскости 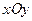 можно подобрать функцию двух переменных, для которой эта фигура будет являться областью определения. можно подобрать функцию двух переменных, для которой эта фигура будет являться областью определения.
Замечание. Для функции трех переменных  аргументом является тройка чисел аргументом является тройка чисел  , которая, как известно, тоже может быть изображена точкой , которая, как известно, тоже может быть изображена точкой  с координатами с координатами  , , 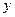 и и  , но уже в трехмерном координатном пространстве , но уже в трехмерном координатном пространстве  . Поэтому для функции трех переменных . Поэтому для функции трех переменных  областью определения будет являться уже объемная фигура в координатном пространстве областью определения будет являться уже объемная фигура в координатном пространстве  , состоящая из точек , состоящая из точек  , координаты которых можно подставлять в формулу , координаты которых можно подставлять в формулу  , которой задается функция. , которой задается функция.
Пример 1. Найти область определения функции 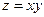 . .
 Решение. Выясним, пары каких чисел Решение. Выясним, пары каких чисел  и и 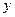 можно подставлять в функцию можно подставлять в функцию 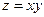 для вычисления ее значения в соответствующей точке. Тогда все точки с этими координатами и будут (по определению) составлять область определения данной функции. Поскольку при вычислении значения функции для вычисления ее значения в соответствующей точке. Тогда все точки с этими координатами и будут (по определению) составлять область определения данной функции. Поскольку при вычислении значения функции 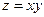 нужно выполнить всего одну операцию умножения, а перемножать можно любые числа, то значение данной функции можно вычислить на любой паре чисел нужно выполнить всего одну операцию умножения, а перемножать можно любые числа, то значение данной функции можно вычислить на любой паре чисел  . Поэтому в область определения входят точки с любыми координатами, т.е. все точки плоскости. Итак, областью определения функции . Поэтому в область определения входят точки с любыми координатами, т.е. все точки плоскости. Итак, областью определения функции 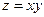 является вся координатная плоскость является вся координатная плоскость 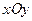 (см. рисунок). (см. рисунок).
Пример 2. Найти область определения функции  . .
Решение. Сначала опять выясним, пары каких чисел  и и 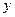 можно подставлять в функцию можно подставлять в функцию  для вычисления ее значения в соответствующей точке. При вычислении значения этой функции нужно выполнить для вычисления ее значения в соответствующей точке. При вычислении значения этой функции нужно выполнить  три операции – дважды извлечение корня и одно сложение. Складывать можно любые числа, а извлекать квадратные корни можно только из неотрицательных чисел. Поэтому подставлять в функцию можно только неотрицательные пары чисел три операции – дважды извлечение корня и одно сложение. Складывать можно любые числа, а извлекать квадратные корни можно только из неотрицательных чисел. Поэтому подставлять в функцию можно только неотрицательные пары чисел  и и 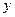 . Таким образом, область определения данной функции составляют только те точки, обе координаты которых неотрицательны. Таковыми являются только точки, лежащие в первой четверти. Таким образом, областью определения функции . Таким образом, область определения данной функции составляют только те точки, обе координаты которых неотрицательны. Таковыми являются только точки, лежащие в первой четверти. Таким образом, областью определения функции  является первая четверть (см. рисунок). является первая четверть (см. рисунок).
Пример 3. Найти область определения функции 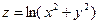 . .
Решение. Для вычисления значения этой функции требуется дважды произвести возведение в квадрат, сложение и взятие логарифма. Только последняя из этих операций (взятие логарифма) выполнима не всегда – получающееся под знаком логарифма число должно быть положительным. Таким образом, значение этой функции можно вычислить для любой пары чисел  и и 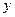 , для которой выполнено: , для которой выполнено: 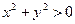 . Поскольку квадраты любых чисел неотрицательны, а сумма двух неотрицательных чисел снова неотрицательна, то для любой пары чисел . Поскольку квадраты любых чисел неотрицательны, а сумма двух неотрицательных чисел снова неотрицательна, то для любой пары чисел  и и 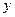 будет будет 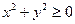 . Поэтому нам остается исключить только те пары чисел . Поэтому нам остается исключить только те пары чисел  и и 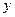 , для которых , для которых  . Сумма двух неотрицательных чисел может дать 0 только в случае, если каждое их слагаемых равно 0. Поэтому . Сумма двух неотрицательных чисел может дать 0 только в случае, если каждое их слагаемых равно 0. Поэтому  только если только если  и и  . Такое может быть выполнено только для одной пары чисел: . Такое может быть выполнено только для одной пары чисел: 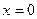 и и  . Точка, имеющая эти числа своими координатами, есть начало координат. Таким образом, областью определения функции . Точка, имеющая эти числа своими координатами, есть начало координат. Таким образом, областью определения функции 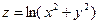 является вся координатная плоскость является вся координатная плоскость 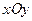 , из которой удалено начало координат. , из которой удалено начало координат.
Для изображения области определения функции двух переменных часто возникает необходимость изобразить на координатной плоскости 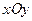 фигуру (обозначим ее, например, буквой фигуру (обозначим ее, например, буквой  ), координаты ), координаты  и и 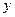 точек которой удовлетворяют некоторому неравенству вида точек которой удовлетворяют некоторому неравенству вида  (знак неравенства может быть и в другую сторону, неравенство может быть и строгое). Это делается по следующей схеме (напоминает метод интервалов при решении неравенств): а) Заменяем данное неравенство на равенство, получаем (знак неравенства может быть и в другую сторону, неравенство может быть и строгое). Это делается по следующей схеме (напоминает метод интервалов при решении неравенств): а) Заменяем данное неравенство на равенство, получаем  ; б) Рисуем кривую (узнав ее по виду уравнения), определяемую этим уравнением ; б) Рисуем кривую (узнав ее по виду уравнения), определяемую этим уравнением  . Эта фигура разделяет координатную плоскость на несколько областей. Для координат всех точек из каждой такой области выполняется в точности одно из неравенств: либо . Эта фигура разделяет координатную плоскость на несколько областей. Для координат всех точек из каждой такой области выполняется в точности одно из неравенств: либо  , либо , либо  . в) Для выбора тех областей, в которых выполняется неравенство нужного типа, проверяем каждую из получившихся областей с помощью пробных точек. Далее будут рассмотрены соответствующие примеры. . в) Для выбора тех областей, в которых выполняется неравенство нужного типа, проверяем каждую из получившихся областей с помощью пробных точек. Далее будут рассмотрены соответствующие примеры.
По аналогичной схеме строится область определения и для функции трех переменных  , если эта область определяется неравенством типа , если эта область определяется неравенством типа  . .
Пример 4. Найти область определения функции  . .
Решение. Значение этой функции можно вычислить для любой пары чисел  и и 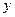 , для которой выполнено: , для которой выполнено:  , т.е. , т.е.  . Таким образом, область определения будет состоять из тех точек координатной плоскости, у которых первая координата (абсцисса) не превосходит второй (ординаты). Для изображения области на координатной плоскости . Таким образом, область определения будет состоять из тех точек координатной плоскости, у которых первая координата (абсцисса) не превосходит второй (ординаты). Для изображения области на координатной плоскости 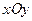 , координаты , координаты  и и 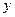 точек которой удовлетворяют неравенству точек которой удовлетворяют неравенству  , действуем по приведенной выше схеме. Заменяя неравенство на равенство, получим , действуем по приведенной выше схеме. Заменяя неравенство на равенство, получим  . Легко вспомнить, что это уравнение прямой, являющейся биссектрисой первой и третьей четверти. Эта прямая делит всю координатную плоскость . Легко вспомнить, что это уравнение прямой, являющейся биссектрисой первой и третьей четверти. Эта прямая делит всю координатную плоскость 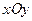 на две области (под этой прямой и над ней). Проверяем каждую из них. В первой области (под прямой) берем, например, точку на две области (под этой прямой и над ней). Проверяем каждую из них. В первой области (под прямой) берем, например, точку  (она лежит на оси (она лежит на оси  справа от начала координат, а потому лежит как раз в области под прямой справа от начала координат, а потому лежит как раз в области под прямой  ) и подставляем ее координаты в требуемое неравенство ) и подставляем ее координаты в требуемое неравенство  . Получаем . Получаем  . Это неверное неравенство, а потому вся область под прямой не будет входить в область определения функции. Берем произвольную точку из области над прямой . Это неверное неравенство, а потому вся область под прямой не будет входить в область определения функции. Берем произвольную точку из области над прямой  , например, , например,  (убедитесь, что точка с такими координатами действительно лежит над прямой (убедитесь, что точка с такими координатами действительно лежит над прямой  ) и подставляем ее координаты в требуемое неравенство ) и подставляем ее координаты в требуемое неравенство  . Получаем . Получаем 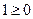 . Это верное числовое неравенство, а потому область над прямой входит в область определения функции. Таким образом, область определения функции . Это верное числовое неравенство, а потому область над прямой входит в область определения функции. Таким образом, область определения функции  есть полуплоскость, лежащая над прямой с уравнением есть полуплоскость, лежащая над прямой с уравнением  (включая точки самой прямой), изображенная на рисунке. (включая точки самой прямой), изображенная на рисунке.
Пример 5. Найти область определения функции  . .
Решение. Значение этой функции можно вычислить для любой пары чисел  и и 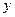 , для которой выполнено: , для которой выполнено:  (под знаком логарифма должны быть положительные числа), т.е. (под знаком логарифма должны быть положительные числа), т.е.  . Для изображения соответствующей области на координатной плоскости . Для изображения соответствующей области на координатной плоскости 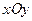 снова действуем по приведенной схеме. Заменяя неравенство на равенство, получим снова действуем по приведенной схеме. Заменяя неравенство на равенство, получим  . Теперь нужно вспомнить, что уравнение вида . Теперь нужно вспомнить, что уравнение вида  есть уравнение окружности радиуса есть уравнение окружности радиуса 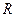 с центром в точке с координатами с центром в точке с координатами 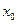 и и  . Поэтому полученное нами уравнение . Поэтому полученное нами уравнение  суть уравнение окружности радиуса 2 с центром в начале координат (так как это уравнение получается из приведенного выше общего уравнения окружности при суть уравнение окружности радиуса 2 с центром в начале координат (так как это уравнение получается из приведенного выше общего уравнения окружности при  , ,  и и  ). Эта окружность делит всю координатную плоскость ). Эта окружность делит всю координатную плоскость 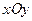 на две области − внутри окружности (это круг радиуса 2 с центром в начале координат) и вне нее. Проверяем каждую из них. В первой области (круге) берем, например, точку на две области − внутри окружности (это круг радиуса 2 с центром в начале координат) и вне нее. Проверяем каждую из них. В первой области (круге) берем, например, точку  − начало координат − и подставляем ее координаты в требуемое неравенство − начало координат − и подставляем ее координаты в требуемое неравенство  : :  , т.е. , т.е.  . Это − верное числовое неравенство, а потому упомянутый круг входит в область определения функции. Проверяем область вне круга, беря в качестве пробной точки, например, точку . Это − верное числовое неравенство, а потому упомянутый круг входит в область определения функции. Проверяем область вне круга, беря в качестве пробной точки, например, точку  и подставляя ее координаты в неравенство и подставляя ее координаты в неравенство  : :  , т.е. , т.е. 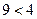 . Это неверное неравенство, а потому вся область вне круга не будет входить в область определения функции. Отдельно проверим точки самой окружности. Для координат любой из таких точек выполнено: . Это неверное неравенство, а потому вся область вне круга не будет входить в область определения функции. Отдельно проверим точки самой окружности. Для координат любой из таких точек выполнено:  . А в область определения входят только точки, координаты которых удовлетворяют неравенству . А в область определения входят только точки, координаты которых удовлетворяют неравенству  . Поэтому точки самой окружности не входят в область определения функции. Таким образом, область определения функции . Поэтому точки самой окружности не входят в область определения функции. Таким образом, область определения функции  есть круг радиуса 2 с центром в начале координат (без границы). Эта область изображена на рисунке. есть круг радиуса 2 с центром в начале координат (без границы). Эта область изображена на рисунке.
 Пример 6. Найти область определения функции Пример 6. Найти область определения функции 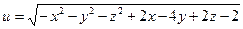 . .
Решение. Теперь исследуется уже функция трех переменных, а потому ее областью определения будет некая объемная фигура в пространстве. Понятно, что область определения такой функции определяется тем, что под корнем должны появляться только неотрицательные числа, т.е. неравенством  . Умножим для удобства обе части этого неравенства на . Умножим для удобства обе части этого неравенства на  (при этом знак неравенства, как известно, меняется на противоположный): (при этом знак неравенства, как известно, меняется на противоположный):  . Группируя слагаемые с . Группируя слагаемые с  , , 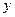 , ,  и дополняя их до полных квадратов, получим (после перенесения числа в правую часть) неравенство: и дополняя их до полных квадратов, получим (после перенесения числа в правую часть) неравенство:
(*)  . .
 Таким образом, нам нужно найти в координатном пространстве Таким образом, нам нужно найти в координатном пространстве  фигуру, состоящую из точек фигуру, состоящую из точек  , координаты которых удовлетворяют неравенству (*). Для этого снова действуем по приведенной схеме, учитывая. Заменяя в (*) знак неравенства на знак равенства, получим , координаты которых удовлетворяют неравенству (*). Для этого снова действуем по приведенной схеме, учитывая. Заменяя в (*) знак неравенства на знак равенства, получим 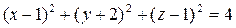 . Теперь нужно из аналитической геометрии вспомнить, что уравнение вида . Теперь нужно из аналитической геометрии вспомнить, что уравнение вида  есть уравнение сферы радиуса есть уравнение сферы радиуса 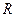 с центром в точке с координатами с центром в точке с координатами 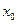 , ,  и и  . Поэтому полученное нами уравнение суть уравнение сферы радиуса 2 с центром в точке с координатами . Поэтому полученное нами уравнение суть уравнение сферы радиуса 2 с центром в точке с координатами 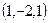 (так как это уравнение получается из приведенного выше общего уравнения сферы при (так как это уравнение получается из приведенного выше общего уравнения сферы при  , ,  , ,  и и  ). Эта сфера делит все координатное пространство ). Эта сфера делит все координатное пространство  на две области − внутри сферы (это шар радиуса 2 с тем же центром) и вне нее. Проверяем каждую из них. В первой области (шаре) берем, например, точку на две области − внутри сферы (это шар радиуса 2 с тем же центром) и вне нее. Проверяем каждую из них. В первой области (шаре) берем, например, точку  (это центр шара – он уж точно внутри него) и подставляем ее координаты в требуемое неравенство (*): (это центр шара – он уж точно внутри него) и подставляем ее координаты в требуемое неравенство (*):  , т.е. , т.е.  . Это − верное числовое неравенство, а потому упомянутый шар входит в область определения функции. Проверяем область вне сферы, беря в качестве пробной точки, например, точку . Это − верное числовое неравенство, а потому упомянутый шар входит в область определения функции. Проверяем область вне сферы, беря в качестве пробной точки, например, точку  и подставляя ее координаты в неравенство (*): и подставляя ее координаты в неравенство (*):  , т.е. , т.е.  . Это неверное неравенство, а потому вся область вне сферы не будет входить в область определения функции. Отдельно проверим точки самой сферы. Для координат любой из таких точек выполнено: . Это неверное неравенство, а потому вся область вне сферы не будет входить в область определения функции. Отдельно проверим точки самой сферы. Для координат любой из таких точек выполнено: 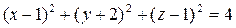 . Поскольку неравенство (*) − нестрогое, то точки самой сферы тоже принадлежат области определения. Таким образом, область определения функции . Поскольку неравенство (*) − нестрогое, то точки самой сферы тоже принадлежат области определения. Таким образом, область определения функции 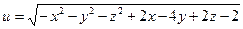 есть шар (с границей) радиуса 2 с центром в точке с координатами есть шар (с границей) радиуса 2 с центром в точке с координатами 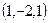 . Эта область изображена на рисунке. . Эта область изображена на рисунке.
График функции двух переменных определим по аналогии с графиком функции одного переменного. Напомним, что графиком функции одного переменного  называется множество точек на координатной плоскости хОу (они образуют некоторую кривую), координаты х и у которых удовлетворяют соотношению называется множество точек на координатной плоскости хОу (они образуют некоторую кривую), координаты х и у которых удовлетворяют соотношению  , задающему функцию. Поскольку в записи функции двух переменных , задающему функцию. Поскольку в записи функции двух переменных  задействованы 3 переменные (x, y и z), то от координатной плоскости придется перейти к координатному пространству. Итак, графиком функции двух переменных задействованы 3 переменные (x, y и z), то от координатной плоскости придется перейти к координатному пространству. Итак, графиком функции двух переменных  называется множество точек в координатном пространстве Oxyz, координаты x, y и z которых удовлетворяют соотношению называется множество точек в координатном пространстве Oxyz, координаты x, y и z которых удовлетворяют соотношению  , которым задается функция. Такое множество точек в координатном пространстве образует уже некоторую поверхность. Поэтому (в отличии от функции одного переменного) график функции двух переменных есть некая поверхность в координатном пространстве Oxyz. , которым задается функция. Такое множество точек в координатном пространстве образует уже некоторую поверхность. Поэтому (в отличии от функции одного переменного) график функции двух переменных есть некая поверхность в координатном пространстве Oxyz.
Пример 7. Определить форму графика функции  и построить его. и построить его.
Решение. По данному выше определению графика функции для его построения нам нужно понять, какую поверхность в пространстве образуют точки, координаты  , , 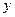 и и  которых удовлетворяют соотношению которых удовлетворяют соотношению  , которым задается функция. Сначала отметим, что координата , которым задается функция. Сначала отметим, что координата  таких точек должна быть неотрицательной: таких точек должна быть неотрицательной:  (так как (так как  , а значение квадратного корня всегда неотрицательно), а потому все такие точки расположены над координатной плоскостью , а значение квадратного корня всегда неотрицательно), а потому все такие точки расположены над координатной плоскостью 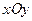 . Далее, возведем обе части данного соотношения . Далее, возведем обе части данного соотношения  в квадрат, получив в квадрат, получив 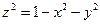 , откуда , откуда  . Точки какой поверхности удовлетворяют этому уравнению? При решении предыдущего примера мы уже вспоминали, что уравнением вида . Точки какой поверхности удовлетворяют этому уравнению? При решении предыдущего примера мы уже вспоминали, что уравнением вида  задаются точки сферы радиуса задаются точки сферы радиуса 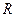 с центром в точке с центром в точке  . Полученное нами соотношение . Полученное нами соотношение  для координат точек графика есть уравнение для координат точек графика есть уравнение  сферы с параметрами сферы с параметрами  , ,  , ,  и и  . Таким образом, точки искомого графика функции лежат на сфере радиуса 1 с центром в начале координат. Учитывая полученное ранее соотношение . Таким образом, точки искомого графика функции лежат на сфере радиуса 1 с центром в начале координат. Учитывая полученное ранее соотношение  , окончательно имеем, что график функции , окончательно имеем, что график функции  есть верхняя часть сферы радиуса 1 с центром в начале координат (см. рисунок). есть верхняя часть сферы радиуса 1 с центром в начале координат (см. рисунок).
Обобщим понятие предела функции одного переменного на функции двух переменных. Число  называется пределом функции называется пределом функции  в точке в точке 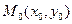 , если при безграничном приближении точки , если при безграничном приближении точки  к точке к точке 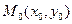  по любому закону (т.е. по любой кривой, ведущей в точку по любому закону (т.е. по любой кривой, ведущей в точку  ) значения функции ) значения функции  безгранично приближаются к одному и тому же числу а. Иллюстрация на рисунке. Записывается этот факт в виде: безгранично приближаются к одному и тому же числу а. Иллюстрация на рисунке. Записывается этот факт в виде: 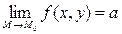 или или  . Это опять «интуитивное» определение предела, выражающее суть этого понятия. Для наших целей этого достаточно, поэтому формального математически строгого определения предела мы не даем. Аналогично определяется понятие предела для функции трех переменных . Это опять «интуитивное» определение предела, выражающее суть этого понятия. Для наших целей этого достаточно, поэтому формального математически строгого определения предела мы не даем. Аналогично определяется понятие предела для функции трех переменных  . .
Дадим понятие непрерывности функции двух переменных, которое тоже вводится по аналогии с определением непрерывности, данного ранее для функции одного переменного. Напомним, как вводилась непрерывность для функции одного переменного. Точка  называлась точкой непрерывности функции называлась точкой непрерывности функции  , если выполнено: , если выполнено:  . Итак, точка . Итак, точка 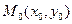 называется точкой непрерывности функции называется точкой непрерывности функции  , если выполнено , если выполнено  , причем точка , причем точка  (в соответствии с данным выше определением предела) может приближаться к точке (в соответствии с данным выше определением предела) может приближаться к точке 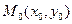 по любому пути. Аналогично, точка по любому пути. Аналогично, точка 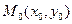 называется точкой разрыва функции называется точкой разрыва функции  , если она не является точкой непрерывности этой функции. Для функции одного переменного классификация точек разрыва была достаточно бедной: разрывы 1 или 2 рода, поскольку есть немного возможностей, каким способом плоская линия (график функции одного переменного) может разорваться в некоторой своей точке. Графиком функции двух переменных является поверхность в пространстве, характер разрывов которой может быть очень разнообразным. Обычно точки разрыва функции образуют целые линии на координатной плоскости хОу. Аналогично случаю одного переменного, если функция двух переменных , если она не является точкой непрерывности этой функции. Для функции одного переменного классификация точек разрыва была достаточно бедной: разрывы 1 или 2 рода, поскольку есть немного возможностей, каким способом плоская линия (график функции одного переменного) может разорваться в некоторой своей точке. Графиком функции двух переменных является поверхность в пространстве, характер разрывов которой может быть очень разнообразным. Обычно точки разрыва функции образуют целые линии на координатной плоскости хОу. Аналогично случаю одного переменного, если функция двух переменных  задана одной формулой, то она непрерывна во всех точках задана одной формулой, то она непрерывна во всех точках  , в которых определена, поэтому точки разрыва могут быть только на линиях, в точках которых функция не определена. , в которых определена, поэтому точки разрыва могут быть только на линиях, в точках которых функция не определена.
Пример 8. Исследовать на непрерывность функцию  . .
Решение. Функция  определена во всех точках координатной плоскости хОу, кроме точек, координаты которых удовлетворяют соотношению определена во всех точках координатной плоскости хОу, кроме точек, координаты которых удовлетворяют соотношению  (в таких точках вычислить функцию нельзя, т.к. знаменатель обращается в 0). Это соотношение, как известно, есть уравнение прямой, проходящей через начало координат и являющейся биссектрисой I и III координатного угла. Эта прямая и образует линию разрывов функции (в таких точках вычислить функцию нельзя, т.к. знаменатель обращается в 0). Это соотношение, как известно, есть уравнение прямой, проходящей через начало координат и являющейся биссектрисой I и III координатного угла. Эта прямая и образует линию разрывов функции  , а в остальных точках координатной плоскости , а в остальных точках координатной плоскости  функция непрерывна. функция непрерывна.
Аналогично определяется понятие точек непрерывности и разрыва для функции трех переменных  . .
Обратимся к важному понятию линий уровня функции двух переменных. Как ранее упоминалось, для функции одной переменной  ее график является самой наглядной и удобной иллюстрацией характера зависимости переменной ее график является самой наглядной и удобной иллюстрацией характера зависимости переменной 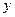 от переменной от переменной  . Для функции двух переменных можно было бы сказать то же самое, но график функции двух переменных (это поверхность!) изображать значительно сложнее. На плоском рисунке поверхность изображается искаженно, а трехмерный макет графика строить сложно и нецелесообразно. Как же наглядно изобразить на плоском рисунке поверхность, являющуюся графиком некоторой функции двух переменных? Можно поступить так же, как поступают при создании (плоских) географических карт, на которых, тем не менее, изображаются горы и впадины, отражается их (гор и впадин) форма. . Для функции двух переменных можно было бы сказать то же самое, но график функции двух переменных (это поверхность!) изображать значительно сложнее. На плоском рисунке поверхность изображается искаженно, а трехмерный макет графика строить сложно и нецелесообразно. Как же наглядно изобразить на плоском рисунке поверхность, являющуюся графиком некоторой функции двух переменных? Можно поступить так же, как поступают при создании (плоских) географических карт, на которых, тем не менее, изображаются горы и впадины, отражается их (гор и впадин) форма.
Для плоского изображения, например, горы, делается следующее. Берется плоскость, параллельная земле (т.е. параллельная координатной плоскости хОу, если эту плоскость пустить по земле) на определенной высоте h от нее, затем сечение поверхности горы этой плоскостью проектируется на плоскость земли (плоскость хОу или плоскость создаваемой карты в некотором масштабе). Получающаяся линия на этой плоскости называется линией уровня данной горы, соответствующей высоте h. Меняя высоту h, получают линии уровня, соответствующие разным высотам. По форме линий уровня можно судить о форме поверхности всей горы.
Поступим аналогично и с поверхностью графика функции  . Возьмем произвольное число С (аналог высоты h) и рассмотрим в координатном пространстве Oxyz соответствующую плоскость, параллельную координатной плоскости хОу и расположенная на высоте (или глубине, если . Возьмем произвольное число С (аналог высоты h) и рассмотрим в координатном пространстве Oxyz соответствующую плоскость, параллельную координатной плоскости хОу и расположенная на высоте (или глубине, если  ) )  от нее (уравнение такой плоскости от нее (уравнение такой плоскости 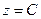 ). Рассмотрим сечение этой плоскостью поверхности-графика функции ). Рассмотрим сечение этой плоскостью поверхности-графика функции  . Это будет линия, состоящая из точек, лежащих одновременно на поверхности и плоскости. Поэтому координаты этих точек должны удовлетворять системе . Это будет линия, состоящая из точек, лежащих одновременно на поверхности и плоскости. Поэтому координаты этих точек должны удовлетворять системе
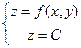
Отсюда получаем 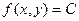 . Это уравнение некоторой линии в плоскости хОу. Все точки этой линии обладают тем очевидным свойством, что наша функция . Это уравнение некоторой линии в плоскости хОу. Все точки этой линии обладают тем очевидным свойством, что наша функция  принимает в них одно и то же значение (равное принимает в них одно и то же значение (равное  ). Итак, линией уровня функции ). Итак, линией уровня функции  (соответствующей некоторому числу (соответствующей некоторому числу  ) называется линия на плоскости хОу, уравнение которой ) называется линия на плоскости хОу, уравнение которой 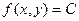 . Во всех точках этой линии значение функции . Во всех точках этой линии значение функции  одинаково (а именно, равно одинаково (а именно, равно  ). ).
Пример 9. Определить форму линий уровня для функции  . .
Решение. Рассмотрим кривые, задаваемые уравнением  . Ясно, что линии уровня могут соответствовать только числам . Ясно, что линии уровня могут соответствовать только числам  (так как квадратный корень может давать только неотрицательные значения). Возводя в квадрат, получим (так как квадратный корень может давать только неотрицательные значения). Возводя в квадрат, получим  . Это, как несложно узнать, уравнение окружностей с центром в . Это, как несложно узнать, уравнение окружностей с центром в  начале координат и радиуса С. Таковыми и являются линии уровня данной функции. Таким образом, линиями уровня являются всевозможные концентрические окружности с центром в начале координат. На рисунке изображены две из них с уравнениями начале координат и радиуса С. Таковыми и являются линии уровня данной функции. Таким образом, линиями уровня являются всевозможные концентрические окружности с центром в начале координат. На рисунке изображены две из них с уравнениями  и и  , соответствующие значениям , соответствующие значениям 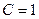 и и  . .
Пример 10. Пусть определена зависимость  урожайности урожайности  неко неко
|



 . Многие реальные зависимости в действительности таковыми и являются. Например:
. Многие реальные зависимости в действительности таковыми и являются. Например:  − площадь круга, зависит только от значения одной переменной
− площадь круга, зависит только от значения одной переменной 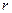 − радиуса круга;
− радиуса круга;  − площадь квадрата, зависит только от одной переменной
− площадь квадрата, зависит только от одной переменной 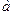 − длины стороны квадрата;
− длины стороны квадрата;  − зависимость пройденного пути от времени (при заданной постоянной скорости
− зависимость пройденного пути от времени (при заданной постоянной скорости 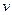 ) − функция только от времени движения
) − функция только от времени движения 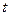 ;
;  − зависимость прибыли
− зависимость прибыли  некоторого производства от вложенных в него средств
некоторого производства от вложенных в него средств  ;
; 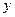 от количества внесенных удобрений
от количества внесенных удобрений  − и так далее. Но в реальности чаще исследуемый фактор зависит не от одного, а от многих других факторов. Площадь прямоугольника
− и так далее. Но в реальности чаще исследуемый фактор зависит не от одного, а от многих других факторов. Площадь прямоугольника  ,
,  − объем параллелепипеда (от 3-х – длин ребер). Более точная зависимость прибыли
− объем параллелепипеда (от 3-х – длин ребер). Более точная зависимость прибыли  (капитал) – средства, вложенные в материалы, оборудование и
(капитал) – средства, вложенные в материалы, оборудование и  (труд) – средства, вложенные в трудовые ресурсы; тогда
(труд) – средства, вложенные в трудовые ресурсы; тогда  . Более точная зависимость урожайности от количества удобрений дифференцирует (в смысле «различает») количество вложенных удобрений разного типа (например, фосфорные и калийные):
. Более точная зависимость урожайности от количества удобрений дифференцирует (в смысле «различает») количество вложенных удобрений разного типа (например, фосфорные и калийные): 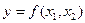 . Поэтому переходим к изучению функций многих переменных. Перенесем известные понятия, проходимые для функций одного переменного, на функции многих переменных (в основном, на примере функций двух и трех переменных). Общая форма записи функций двух и трех переменных:
. Поэтому переходим к изучению функций многих переменных. Перенесем известные понятия, проходимые для функций одного переменного, на функции многих переменных (в основном, на примере функций двух и трех переменных). Общая форма записи функций двух и трех переменных:  и
и  – по аналогии с функцией одного переменного
– по аналогии с функцией одного переменного  называется функцией переменных
называется функцией переменных 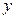 , если имеется правило, по которому каждой (допустимой!) паре числовых значений переменных
, если имеется правило, по которому каждой (допустимой!) паре числовых значений переменных  ставится в соответствие некоторое (одно) числовое значение переменной
ставится в соответствие некоторое (одно) числовое значение переменной  называется функцией трех переменных
называется функцией трех переменных  , если имеется правило, по которому каждой допустимой тройке числовых значений переменных
, если имеется правило, по которому каждой допустимой тройке числовых значений переменных  ставится в соответствие некоторое (одно) числовое значение переменной
ставится в соответствие некоторое (одно) числовое значение переменной  Для функции одного переменного
Для функции одного переменного  является следующее подмножество числовой прямой:
является следующее подмножество числовой прямой:  . Таким образом, область определения функции одного переменного – некоторое подмножество точек (числовой) прямой. Для функции же двух переменных
. Таким образом, область определения функции одного переменного – некоторое подмножество точек (числовой) прямой. Для функции же двух переменных 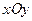 . Действительно, каждая пара чисел
. Действительно, каждая пара чисел  на координатной плоскости
на координатной плоскости  , то эту функцию нельзя вычислить при
, то эту функцию нельзя вычислить при  (другими словами, в точке
(другими словами, в точке  ), поскольку в этом случае под логарифмом получается отрицательное число. Если собрать все пары чисел
), поскольку в этом случае под логарифмом получается отрицательное число. Если собрать все пары чисел  с координатами
с координатами  . Поэтому для функции трех переменных
. Поэтому для функции трех переменных 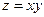 .
. Решение. Выясним, пары каких чисел
Решение. Выясним, пары каких чисел  .
. три операции – дважды извлечение корня и одно сложение. Складывать можно любые числа, а извлекать квадратные корни можно только из неотрицательных чисел. Поэтому подставлять в функцию можно только неотрицательные пары чисел
три операции – дважды извлечение корня и одно сложение. Складывать можно любые числа, а извлекать квадратные корни можно только из неотрицательных чисел. Поэтому подставлять в функцию можно только неотрицательные пары чисел 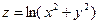 .
.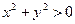 . Поскольку квадраты любых чисел неотрицательны, а сумма двух неотрицательных чисел снова неотрицательна, то для любой пары чисел
. Поскольку квадраты любых чисел неотрицательны, а сумма двух неотрицательных чисел снова неотрицательна, то для любой пары чисел 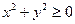 . Поэтому нам остается исключить только те пары чисел
. Поэтому нам остается исключить только те пары чисел  . Сумма двух неотрицательных чисел может дать 0 только в случае, если каждое их слагаемых равно 0. Поэтому
. Сумма двух неотрицательных чисел может дать 0 только в случае, если каждое их слагаемых равно 0. Поэтому  и
и  . Такое может быть выполнено только для одной пары чисел:
. Такое может быть выполнено только для одной пары чисел: 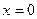 и
и  . Точка, имеющая эти числа своими координатами, есть начало координат. Таким образом, областью определения функции
. Точка, имеющая эти числа своими координатами, есть начало координат. Таким образом, областью определения функции  ), координаты
), координаты  (знак неравенства может быть и в другую сторону, неравенство может быть и строгое). Это делается по следующей схеме (напоминает метод интервалов при решении неравенств): а) Заменяем данное неравенство на равенство, получаем
(знак неравенства может быть и в другую сторону, неравенство может быть и строгое). Это делается по следующей схеме (напоминает метод интервалов при решении неравенств): а) Заменяем данное неравенство на равенство, получаем  ; б) Рисуем кривую (узнав ее по виду уравнения), определяемую этим уравнением
; б) Рисуем кривую (узнав ее по виду уравнения), определяемую этим уравнением  . в) Для выбора тех областей, в которых выполняется неравенство нужного типа, проверяем каждую из получившихся областей с помощью пробных точек. Далее будут рассмотрены соответствующие примеры.
. в) Для выбора тех областей, в которых выполняется неравенство нужного типа, проверяем каждую из получившихся областей с помощью пробных точек. Далее будут рассмотрены соответствующие примеры. .
. .
. , т.е.
, т.е.  . Таким образом, область определения будет состоять из тех точек координатной плоскости, у которых первая координата (абсцисса) не превосходит второй (ординаты). Для изображения области на координатной плоскости
. Таким образом, область определения будет состоять из тех точек координатной плоскости, у которых первая координата (абсцисса) не превосходит второй (ординаты). Для изображения области на координатной плоскости  . Легко вспомнить, что это уравнение прямой, являющейся биссектрисой первой и третьей четверти. Эта прямая делит всю координатную плоскость
. Легко вспомнить, что это уравнение прямой, являющейся биссектрисой первой и третьей четверти. Эта прямая делит всю координатную плоскость  (она лежит на оси
(она лежит на оси  . Это неверное неравенство, а потому вся область под прямой не будет входить в область определения функции. Берем произвольную точку из области над прямой
. Это неверное неравенство, а потому вся область под прямой не будет входить в область определения функции. Берем произвольную точку из области над прямой  (убедитесь, что точка с такими координатами действительно лежит над прямой
(убедитесь, что точка с такими координатами действительно лежит над прямой 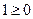 . Это верное числовое неравенство, а потому область над прямой входит в область определения функции. Таким образом, область определения функции
. Это верное числовое неравенство, а потому область над прямой входит в область определения функции. Таким образом, область определения функции  .
. (под знаком логарифма должны быть положительные числа), т.е.
(под знаком логарифма должны быть положительные числа), т.е.  . Для изображения соответствующей области на координатной плоскости
. Для изображения соответствующей области на координатной плоскости  . Теперь нужно вспомнить, что уравнение вида
. Теперь нужно вспомнить, что уравнение вида  есть уравнение окружности радиуса
есть уравнение окружности радиуса 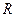 с центром в точке с координатами
с центром в точке с координатами 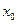 и
и  . Поэтому полученное нами уравнение
. Поэтому полученное нами уравнение  ,
,  и
и  ). Эта окружность делит всю координатную плоскость
). Эта окружность делит всю координатную плоскость  − начало координат − и подставляем ее координаты в требуемое неравенство
− начало координат − и подставляем ее координаты в требуемое неравенство  , т.е.
, т.е.  . Это − верное числовое неравенство, а потому упомянутый круг входит в область определения функции. Проверяем область вне круга, беря в качестве пробной точки, например, точку
. Это − верное числовое неравенство, а потому упомянутый круг входит в область определения функции. Проверяем область вне круга, беря в качестве пробной точки, например, точку  и подставляя ее координаты в неравенство
и подставляя ее координаты в неравенство  , т.е.
, т.е. 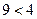 . Это неверное неравенство, а потому вся область вне круга не будет входить в область определения функции. Отдельно проверим точки самой окружности. Для координат любой из таких точек выполнено:
. Это неверное неравенство, а потому вся область вне круга не будет входить в область определения функции. Отдельно проверим точки самой окружности. Для координат любой из таких точек выполнено:  Пример 6. Найти область определения функции
Пример 6. Найти область определения функции 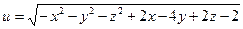 .
. . Умножим для удобства обе части этого неравенства на
. Умножим для удобства обе части этого неравенства на  (при этом знак неравенства, как известно, меняется на противоположный):
(при этом знак неравенства, как известно, меняется на противоположный):  . Группируя слагаемые с
. Группируя слагаемые с  .
. Таким образом, нам нужно найти в координатном пространстве
Таким образом, нам нужно найти в координатном пространстве 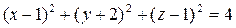 . Теперь нужно из аналитической геометрии вспомнить, что уравнение вида
. Теперь нужно из аналитической геометрии вспомнить, что уравнение вида  есть уравнение сферы радиуса
есть уравнение сферы радиуса  . Поэтому полученное нами уравнение суть уравнение сферы радиуса 2 с центром в точке с координатами
. Поэтому полученное нами уравнение суть уравнение сферы радиуса 2 с центром в точке с координатами 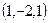 (так как это уравнение получается из приведенного выше общего уравнения сферы при
(так как это уравнение получается из приведенного выше общего уравнения сферы при  ,
,  ,
,  и
и  (это центр шара – он уж точно внутри него) и подставляем ее координаты в требуемое неравенство (*):
(это центр шара – он уж точно внутри него) и подставляем ее координаты в требуемое неравенство (*):  , т.е.
, т.е.  . Это − верное числовое неравенство, а потому упомянутый шар входит в область определения функции. Проверяем область вне сферы, беря в качестве пробной точки, например, точку
. Это − верное числовое неравенство, а потому упомянутый шар входит в область определения функции. Проверяем область вне сферы, беря в качестве пробной точки, например, точку  и подставляя ее координаты в неравенство (*):
и подставляя ее координаты в неравенство (*):  , т.е.
, т.е.  . Это неверное неравенство, а потому вся область вне сферы не будет входить в область определения функции. Отдельно проверим точки самой сферы. Для координат любой из таких точек выполнено:
. Это неверное неравенство, а потому вся область вне сферы не будет входить в область определения функции. Отдельно проверим точки самой сферы. Для координат любой из таких точек выполнено:  называется множество точек на координатной плоскости хОу (они образуют некоторую кривую), координаты х и у которых удовлетворяют соотношению
называется множество точек на координатной плоскости хОу (они образуют некоторую кривую), координаты х и у которых удовлетворяют соотношению  и построить его.
и построить его. (так как
(так как 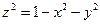 , откуда
, откуда  . Точки какой поверхности удовлетворяют этому уравнению? При решении предыдущего примера мы уже вспоминали, что уравнением вида
. Точки какой поверхности удовлетворяют этому уравнению? При решении предыдущего примера мы уже вспоминали, что уравнением вида  задаются точки сферы радиуса
задаются точки сферы радиуса  . Полученное нами соотношение
. Полученное нами соотношение  сферы с параметрами
сферы с параметрами  и
и  . Таким образом, точки искомого графика функции лежат на сфере радиуса 1 с центром в начале координат. Учитывая полученное ранее соотношение
. Таким образом, точки искомого графика функции лежат на сфере радиуса 1 с центром в начале координат. Учитывая полученное ранее соотношение  называется пределом функции
называется пределом функции 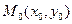 , если при безграничном приближении точки
, если при безграничном приближении точки  к точке
к точке  по любому закону (т.е. по любой кривой, ведущей в точку
по любому закону (т.е. по любой кривой, ведущей в точку  ) значения функции
) значения функции 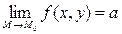 или
или  . Это опять «интуитивное» определение предела, выражающее суть этого понятия. Для наших целей этого достаточно, поэтому формального математически строгого определения предела мы не даем. Аналогично определяется понятие предела для функции трех переменных
. Это опять «интуитивное» определение предела, выражающее суть этого понятия. Для наших целей этого достаточно, поэтому формального математически строгого определения предела мы не даем. Аналогично определяется понятие предела для функции трех переменных  называлась точкой непрерывности функции
называлась точкой непрерывности функции  . Итак, точка
. Итак, точка  , причем точка
, причем точка  .
. функция непрерывна.
функция непрерывна. )
)  от нее (уравнение такой плоскости
от нее (уравнение такой плоскости 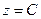 ). Рассмотрим сечение этой плоскостью поверхности-графика функции
). Рассмотрим сечение этой плоскостью поверхности-графика функции 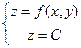
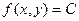 . Это уравнение некоторой линии в плоскости хОу. Все точки этой линии обладают тем очевидным свойством, что наша функция
. Это уравнение некоторой линии в плоскости хОу. Все точки этой линии обладают тем очевидным свойством, что наша функция  .
.  . Ясно, что линии уровня могут соответствовать только числам
. Ясно, что линии уровня могут соответствовать только числам  (так как квадратный корень может давать только неотрицательные значения). Возводя в квадрат, получим
(так как квадратный корень может давать только неотрицательные значения). Возводя в квадрат, получим  . Это, как несложно узнать, уравнение окружностей с центром в
. Это, как несложно узнать, уравнение окружностей с центром в  начале координат и радиуса С. Таковыми и являются линии уровня данной функции. Таким образом, линиями уровня являются всевозможные концентрические окружности с центром в начале координат. На рисунке изображены две из них с уравнениями
начале координат и радиуса С. Таковыми и являются линии уровня данной функции. Таким образом, линиями уровня являются всевозможные концентрические окружности с центром в начале координат. На рисунке изображены две из них с уравнениями  и
и  , соответствующие значениям
, соответствующие значениям 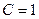 и
и  .
.


